математическое моделирование. 7915726_мат_мод_испр. Используя заданную функцию f(x), которая выбирается из таблицы 1 по числу N
 Скачать 191.88 Kb.
|
Задание 1.Используя заданную функцию f(x), которая выбирается из таблицы № 1 по числу N10, рассчитать 5 точек в интервале [а, b/4], которые использовать как узлы интерполяции. Выбрать точку х внутри этого интервала, в которой восстановить значение функции с помощью заданного метода интерполяции. Метод интерполяции выбрать по числу N4+1 из следующего общего списка методов интерполяции: последние две цифры = 72 => N10 = 2, N4+1 = 1 Метод Лагранжа;
f(x) = ln(x+1)sin(x) интервал [0;2,5] f(0) = ln(1)*sin(0) = 0 f(0,625) = ln(0,625+1)*sin(0,625) = 0,284 f(1,25) = ln(1,25+1)*sin(1,25) = 0,77 f(1,875) = ln(1,875+1)*sin(1,875) = 1,0 f(2,5) = ln(2,5+1)*sin(2,5) = 0,75 В  общем виде интерполяционный многочлен в форме Лагранжа записывается в следующем виде: Полином Лагранжа для пяти точек  В общем виде L5(x) = 0,05477*x^4-0,5118*x^3+1,0678*x^2-0,02627*x Пусть х = 1 P(0) = -0,034 P(0,625) = (1-0)*(1-1,25)*(1-1,875)*(1-2,5)/((0,625-0)*(0,625-1,25)*(0,625-1,875)*(0,625-2,5)) = 0,3584 P(1,25) = (1-0)*(1-0,625)*(1-1,875)*(1-2,5)/((1,25-0)*(1,25-0,625)*(1,25-1,875)*(1,25-2,5)) = 0,8064 P(1,875) = (1-0)*(1-0,625)*(1-1,25)*(1-2,5)/((1,875-0)*(1,875-0,625)*(1,875 -1,25)*(1,875-2,5)) = -0,1536 P(2,5) = (1-0)*(1-0,625)*(1-1,25)*(1-1,875)/((2,5-0)*(2,5-0,625)*(2,5-1,25)*(2,5-1,875)) = 0,0224 L5(1) = 0*(-0,034)+0,284*0,3584+0,7696*0,8064+1,0076*-0,1536+0,7497*0,0224 = 0,5844 Сравним f(1) = ln(1+1)*sin(1) = 0,5833 Δ = (0,5833-0,5844)/0,5833 = 0,0019 (0,2%) Результат вполне удовлетворительный. Проверим в MathCad 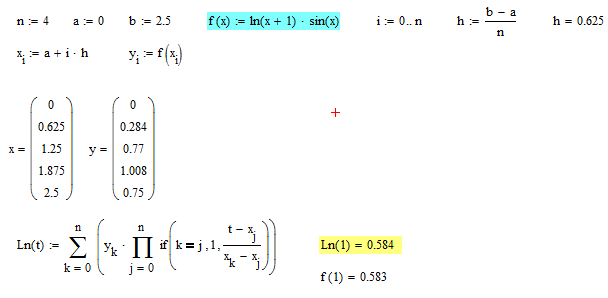 Решения совпали Задание 2.Используя полученные на предыдущем этапе точки построить аппроксимирующие полиномы второго порядка у = d2х2 + d1x + d0 методом наименьших квадратов при всех одинаковых весовых коэффициентах и при весовом коэффициенте в третьей точке в 3 раза большем, чем в остальных (т.е. при 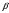 3=3). Получить среднеквадратичную погрешность аппроксимации, величину квадратичного критерия близости и расчётное значение y в третьей точке. Сравнить полученные результаты. Сделать выводы о том, устраивает ли полученное аппроксимирующее уравнение второго порядка по погрешности, сравнивая среднеквадратичную погрешность с заданной в обоих случаях, т.е. и при всех одинаковых весовых коэффициентах и при 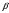3=3. Если результат не утраивает, то, что делать в таком случае дальше. 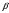Также проанализировать, как повлияло введение весового коэффициента 3=3 на точность аппроксимации в третьей точке (по величине абсолютной погрешности в этой точке) и на точность аппроксимации в целом, (по величине критерия близости). Примечание: Задача аппроксимации, таким образом, выполняется дважды. В обоих случаях необходимо привести выводы всех расчётных формул и алгоритм расчёта, а не просто результат по готовому пакету программ. При решении разного рода задач, часто возникает необходимость описать в виде функциональной зависимости связь между величинами, заданными таблично или в виде набора точек (xi, yi), где i = 0, ..., n. Как правило, эти табличные данные получены экспериментально и имеют погрешности. При аппроксимации желательно получить относительно простую функциональную зависимость (например, многочлен), которая позволила бы «сгладить» экспериментальные погрешности, вычислять значения функции в точках, не содержащихся в исходной таблице. Эта функциональная зависимость должна с достаточной точностью соответствовать исходной табличной зависимости. В качестве критерия точности чаще всего используют критерий наименьших квадратов, т.е. определяют такую функциональную зависимость f(x), при которой  т.е., обращается в минимум. Рассмотрим в качестве функциональной зависимости квадратичную функцию:  Функция R(a, b, c) будет принимать минимальное значение, если частные производные обращаются в нуль: 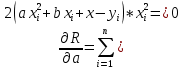 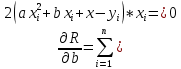  Собираем коэффициенты при неизвестных a, b, c получаем систему уравнений: 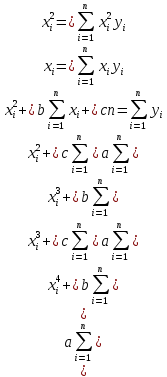 Запишем систему в матричном виде: AX = B   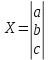 Тогда, решение можно записать в виде: X = A-1B A-1 – обратная матрица Для наших данных
Построим расчетную таблицу
Тогда: 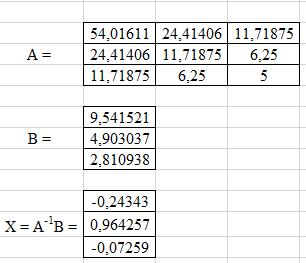 Аппроксимирующий полином второго порядка при равенстве весовых коэффициентов имеет вид: y = -0,24343*x^2+0,964257*x-0,07259 Составим таблицу, в которую запишем как расчётные у, так и значения y заданные. Таблица 4 – Значения f(x), yрасч при равных коэффициентах
Квадратичный критерий близости:  Среднеквадратичная погрешность аппроксимации:  δ = (0,04919/5)^0,5 = 0,1 Определение аппроксимирующей функции при помощи метода наименьших квадратов при неравных весовых коэффициентах d1= d2= d4 = d5=1; d3=3 В этом случае система уравнений, реализующая метод наименьших квадратов запишется в виде: 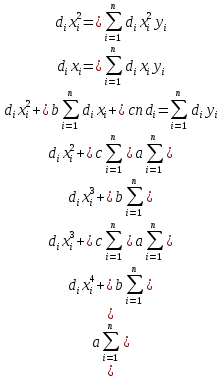 Построим расчетную таблицу
Тогда: 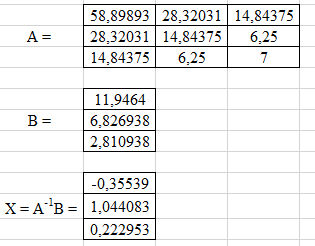 Аппроксимирующий полином второго порядка при неравенстве весовых коэффициентов имеет вид: y = -0,355*x^2+1,0441*x-0,223 Составим таблицу, в которую запишем как расчётные у, так и значения y заданные. Таблица 4 – Значения f(x), yрасч при равных коэффициентах
Квадратичный критерий близости: Среднеквадратичная погрешность аппроксимации: δ = (0,32/5)^0,5 = 0,253 Построим графики 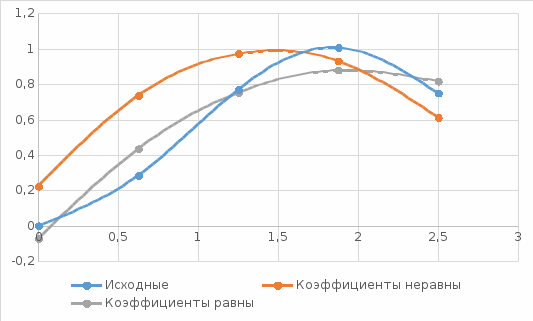 Рис. 1 - Графики аппроксимирующих полиномов и исходной функции Расчетные значения для равных коэффициентов: f(1.25) = -0,24343*1,25^2+0,964257*1,25-0,07259= 0,752 Расчетные значения для неравных коэффициентов: f(1.25) = -0,355*x^2+1,0441*x-0,223 = 0.973 Расчетные значения для исходной функции: f(1,25) = ln(1,25+1)*sin(1,25) = 0,77 Вывод Сравнивая расчетные значения аппроксимирующих функций в третьей точке x = 1,25 и построенных графиков функций (рисунок 1), можно сделать вывод, что аппроксимирующий полином с весовым коэффициентом 3 при х = 1,25 менее точно описывает исходную функцию в окрестности этой точки. Снижение точности в одной точке вызывает увеличение среднеквадратической погрешности, а также величину квадратичного критерия близости, что связано с ухудшением аппроксимации в остальных точках. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||