математическое моделирование. 7915726_мат_мод_испр. Используя заданную функцию f(x), которая выбирается из таблицы 1 по числу N
 Скачать 191.88 Kb. Скачать 191.88 Kb.
|
Задание 3.Дано уравнение f(х) = 0. Отделить корни в интервале [а, b] и уточнить один из них (любой на выбор) заданным методом. Разработать блок-схему алгоритма используемого метода. Результаты представить в виде таблиц (i - хi - f(хi)), и графиков в координатах хi - f(хi), где i – номер шага (итерации). Отделение корней произвести аналитическим или графическим методом, если аналитический метод окажется затруднительным. Уточнение корней произвести одним методом. Метод уточнения корней выбрать по числу N6+1 из общего списка методов: Метод сканирования. Отделим корни графически 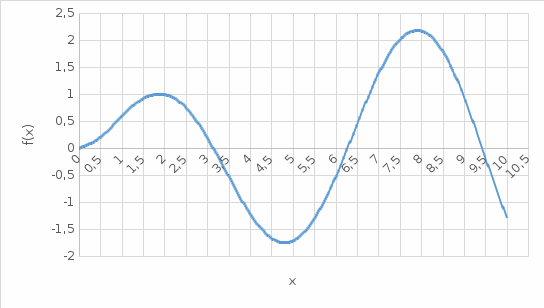 Рис. 2 График функции f(x)=ln(x+1)*sin(x) на интервале [0;10] блок-схема метода сканирования 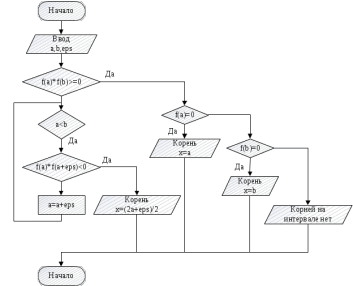 Имеем четыре корня первый корень тривиальный х = 0 второй корень локализован на интервале [3;3,5] третий корень локализован на интервале [6;6,5] четвертый корень локализован на интервале [9;9,5] Ищем корень на интервале [6;6,5] с точностью 0.01 В методе сканирования используется табличный способ отделения корней. Отрезок локализации [a, b] делится на малые отрезки длиной, равной заданной погрешности нахождения корня ε, на концах этих отрезков вычисляются значения функции f(x) . На каждом из этих отрезков проверяется условие и в случае его выполнения выбирается отрезок, где функция меняет знак (или точно равна нулю). В качестве решения можно взять любую точку выделенного отрезка, левую или правую границу этого отрезка или середину отрезка x*=(x(i)+x(i+1))/2, что гораздо лучше Сделаем пару итерация х1 = 6: f(6)=ln(6+1)*sin(6) = -0,5437; х2 = 6,01: f(6,01)=ln(6,01+1)*sin(6,01) = -0,5254; f(6)* f(6,01) > 0 => Корня нет х3 = 6,02: f(6,02)=ln(6,02+1)*sin(6,02) = -0,507; f(6,01)* f(6,02) > 0 => Корня нет и т.д. Строим таблицу
Как видим из таблицы – функция меняет знак в диапазоне 6,28-6,29, таким образом корень х = (6,28+6,29)/2 = 6,285 Решение в MathCad дает 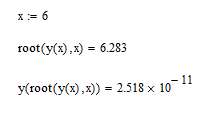 Мы получили решение с вполне удовлетворительной точностью. |
