математическое моделирование. 7915726_мат_мод_испр. Используя заданную функцию f(x), которая выбирается из таблицы 1 по числу N
 Скачать 191.88 Kb. Скачать 191.88 Kb.
|
Задание 7.Решить дифференциальное уравнение у' = f(х) + ху при заданных начальных условиях хо = а, у(хо)= у(а) = 0 в заданных пределах [a, b] с шагом не менее (b - а)/ 10. Метод численного решения дифференциального уравнения выбрать по числу N3+1 из следующего списка методов: 1. Методы Эйлера у' = ln(x+1)*sin(x) + х*у хо = 0, у(0) = 0 h = 1 Решение yi+1 = yi + h·f(xi, yi) Приведенное выше соотношение является расчётной формулой метода Эйлера численного решения задачи Коши. Вычислив yi , i = 0,1,..,n получим таблицу значений решения в точках xi , i = 0,1,..,n Погрешность формулы равна o(h2). К сожалению, метод Эйлера накапливает ошибку от шага к шагу. Первый шаг x0 = 0; y0 = 0 y1 = 0+ ln(0+1)*sin(0) + 0*0 = 0 Первый шаг x1 = 1; y1 = 0 y2 = 0+ ln(1+1)*sin(1) + 1*0 = 0,583 Третий шаг x2 = 2; y2 = 0,583 y3 = 3+ ln(2+1)*sin(2) + 2*0,583 = 2,165 Остальные шаги сведем в таблицу
Модифицированный метод Эйлера y*i+1 = yi+h*f(xi,yi) yi+1 = yi+h/2*(f(xi,yi) + f(xi+1,y*i+1)) Расчеты представим в таблице
В заключение приведем решение методом Рунге-Кутты, реализованное в MathCad 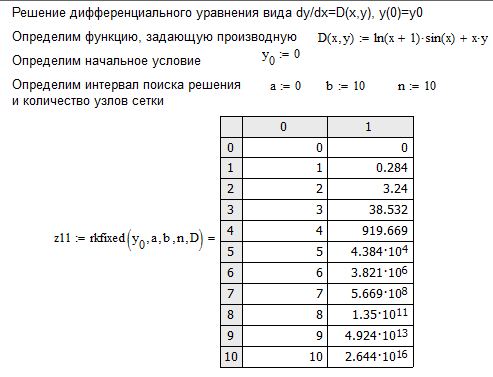 Как видим расхождение между наиболее точным методом Рунге-Кутты и методом Эйлера весьма существенны, особенно в конце интервала. |
