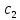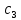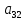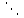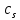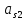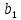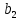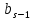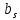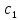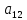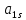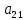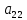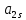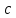Практическая работа решение дифференциальных уравнений. Содержание практической работы. Решение интеграла дифференциального уравнения классическим методом Рунге кутты четвертого порядка
 Скачать 35.95 Kb. Скачать 35.95 Kb.
|
|
Содержание практической работы: Теоретическая часть. Решение интеграла дифференциального уравнения классическим методом Рунге- Кутты четвертого порядка. Используемая литература. Теоретическая часть. Методы Рунге- Кутты- большой класс численных методов решения задачи Коши для обыкновенных дифференциальных уравнений и их систем. Первые методы данного класса были предложены около 1900 года немецкими математиками К. Рунге и М. В. Куттой. К классу методов Рунге- Кутты относятся явный метод Эйлера и модифицированный метод Эйлера с пересчётом, которые представляют собой соответственно методы первого и второго порядка точности. Существуют стандартные явные методы третьего порядка точности, не получившие широкого распространения. Наиболее часто используется и реализован в различных математических пакетах (Maple, MathCAD, Maxima) классический метод Рунге- Кутты, имеющий четвёртый порядок точности. При выполнении расчётов с повышенной точностью всё чаще применяются методы пятого и шестого порядков точности. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями. Методы седьмого порядка должны иметь по меньшей мере девять стадий, а методы восьмого порядка — не менее 11 стадий. Для методов девятого и более высоких порядков (не имеющих, впрочем, большой практической значимости) неизвестно, сколько стадий необходимо для достижения соответствующего порядка точности. Обыкновенное дифференциальное уравнение (ОДУ)- это дифференциальные уравнения для функции от одной переменной. (Этим оно отличается от уравнения в частных производных, где неизвестная — это функция нескольких переменных.) Таким образом, ОДУ- это уравнения вида:{\displaystyle F(x,y,y',y'',…,y^{(n)})=0,\qquad (1)} 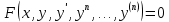 Где y(x) {\displaystyle y(x)} - неизвестная функция, зависящая от независимой переменной {\displaystyle x}x, штрих означает дифференцирование по x{\displaystyle x}. Число n{\displaystyle n} (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения). Классический метод Рунге- Кутты четвертого порядка. Метод Рунге — Кутты четвёртого порядка при вычислениях с постоянным шагом интегрирования столь широко распространён, что его часто называют просто методом Рунге — Кутты. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка. (Далее  ). ).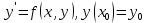 Тогда приближенное значение в последующих точках вычисляется по итерационной формуле: 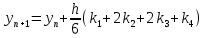 Вычисление нового значения проходит в четыре стадии: 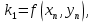 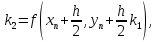 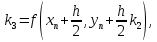 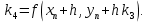 Где{\displaystyle h} 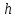 - величина шага сетки по - величина шага сетки по  {\displaystyle x}. {\displaystyle x}.Этот метод имеет четвёртый порядок точности. Это значит, что ошибка на одном шаге имеет порядок  , а суммарная ошибка на конечном интервале интегрирования имеет порядок , а суммарная ошибка на конечном интервале интегрирования имеет порядок 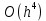 . .Явные методы Рунге- Кутты. Семейство явных методов Рунге — Кутты является обобщением как явного метода Эйлера, так и классического метода Рунге — Кутты четвёртого порядка. Оно задаётся формулами:{\displaystyle {\textbf {y}}_{n+1}={\textbf {y}}_{n}+h\sum _{i=1}^{s}b_{i}{\textbf {k}}_{i},}  , ,Где 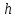 - {\displaystyle h}величина шага сетки по - {\displaystyle h}величина шага сетки по  {\displaystyle x} и вычисление нового значения проходит в {\displaystyle x} и вычисление нового значения проходит в  {\displaystyle s} этапов: {\displaystyle s} этапов: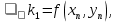 {\displaystyle {\begin{array}{ll}{\textbf {k}}_{1}=&{\textbf {f}}(x_{n},{\textbf {y}}_{n}),\\{\textbf {k}}_{2}=&{\textbf {f}}(x_{n}+c_{2}h,{\textbf {y}}_{n}+a_{21}h{\textbf {k}}_{1}),\\\cdots &\\{\textbf {k}}_{s}=&{\textbf {f}}(x_{n}+c_{s}h,{\textbf {y}}_{n}+a_{s1}h{\textbf {k}}_{1}+a_{s2}h{\textbf {k}}_{2}+\cdots +a_{s,s-1}h{\textbf {k}}_{s-1})\end{array}}} {\displaystyle {\begin{array}{ll}{\textbf {k}}_{1}=&{\textbf {f}}(x_{n},{\textbf {y}}_{n}),\\{\textbf {k}}_{2}=&{\textbf {f}}(x_{n}+c_{2}h,{\textbf {y}}_{n}+a_{21}h{\textbf {k}}_{1}),\\\cdots &\\{\textbf {k}}_{s}=&{\textbf {f}}(x_{n}+c_{s}h,{\textbf {y}}_{n}+a_{s1}h{\textbf {k}}_{1}+a_{s2}h{\textbf {k}}_{2}+\cdots +a_{s,s-1}h{\textbf {k}}_{s-1})\end{array}}}   Конкретный метод определяется числом  {\displaystyle s} и коэффициентами {\displaystyle s} и коэффициентами 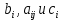 {\displaystyle b_{i},a_{ij}}{\displaystyle c_{i}}. Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Батчера):{\displaystyle {\begin{array}{c|ccccc}0&&&&&\\c_{2}&a_{21}&&&&\\c_{3}&a_{31}&a_{32}&&&\\\vdots &\vdots &\vdots &\ddots &&\\c_{s}&a_{s1}&a_{s2}&\dots &a_{ss-1}&\\\hline &b_{1}&b_{2}&\dots &b_{s-1}&b_{s}\end{array}}} {\displaystyle b_{i},a_{ij}}{\displaystyle c_{i}}. Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Батчера):{\displaystyle {\begin{array}{c|ccccc}0&&&&&\\c_{2}&a_{21}&&&&\\c_{3}&a_{31}&a_{32}&&&\\\vdots &\vdots &\vdots &\ddots &&\\c_{s}&a_{s1}&a_{s2}&\dots &a_{ss-1}&\\\hline &b_{1}&b_{2}&\dots &b_{s-1}&b_{s}\end{array}}}
Для коэффициентов метода Рунге- Кутты должны быть выполнены условия 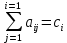 {\displaystyle \sum _{j=1}^{i-1}a_{ij}=c_{i}} для {\displaystyle \sum _{j=1}^{i-1}a_{ij}=c_{i}} для  {\displaystyle i=2,\ldots ,s}. Если требуется, чтобы метод имел порядок {\displaystyle i=2,\ldots ,s}. Если требуется, чтобы метод имел порядок 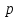 {\displaystyle p}, то следует также обеспечить условие: {\displaystyle p}, то следует также обеспечить условие: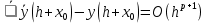 ,{\displaystyle {\bar {\textbf {y}}}(h+x_{0})-{\textbf {y}}(h+x_{0})=O(h^{p+1}),} ,{\displaystyle {\bar {\textbf {y}}}(h+x_{0})-{\textbf {y}}(h+x_{0})=O(h^{p+1}),}Где{\displaystyle {\bar {\textbf {y}}}(h+x_{0})} 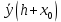 - приближение, полученное по методу Рунге- Кутты. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений относительно коэффициентов метода. - приближение, полученное по методу Рунге- Кутты. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений относительно коэффициентов метода.Неявные методы Рунге- Кутты. Все до сих пор упомянутые методы Рунге- Кутты являются явными методами. К сожалению, явные методы Рунге- Кутты, как правило, непригодны для решения жестких уравнений из-за малой области их абсолютной устойчивости. Неустойчивость явных методов Рунге- Кутты создаёт весьма серьёзные проблемы и при решении дифференциальных уравнений в частных производных. Неустойчивость явных методов Рунге- Кутты мотивировала развитие неявных методов. Неявный метод Рунге- Кутты имеет вид: 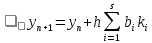 ,{\displaystyle y_{n+1}=y_{n}+h\sum _{i=1}^{s}b_{i}k_{i},} ,{\displaystyle y_{n+1}=y_{n}+h\sum _{i=1}^{s}b_{i}k_{i},}Где 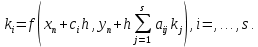 {\displaystyle k_{i}=f{\bigl (}x_{n}+c_{i}h,y_{n}+h\sum _{j=1}^{s}a_{ij}k_{j}{\bigr )},\quad i=1,\ldots ,s.} {\displaystyle k_{i}=f{\bigl (}x_{n}+c_{i}h,y_{n}+h\sum _{j=1}^{s}a_{ij}k_{j}{\bigr )},\quad i=1,\ldots ,s.}Явный метод характерен тем, что матрица коэффициентов {\displaystyle a_{ij}} для него имеет нижний треугольный вид (включая и нулевую главную диагональ)- в отличие от неявного метода, где матрица имеет произвольный вид. Это также видно по таблице Батчера.
= {\displaystyle {\begin{array}{c|cccc}c_{1}&a_{11}&a_{12}&\dots &a_{1s}\\c_{2}&a_{21}&a_{22}&\dots &a_{2s}\\\vdots &\vdots &\vdots &\ddots &\vdots \\c_{s}&a_{s1}&a_{s2}&\dots &a_{ss}\\\hline &b_{1}&b_{2}&\dots &b_{s}\\\end{array}}={\begin{array}{c|c}\mathbf {c} &A\\\hline &\mathbf {b^{T}} \\\end{array}}}Следствием этого различия является необходимость на каждом шагу решать систему уравнений для 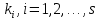 {\displaystyle k_{i},i=1,2,...,s}, где {\displaystyle k_{i},i=1,2,...,s}, где  {\displaystyle s}- число стадий. Это увеличивает вычислительные затраты, однако при достаточно малом {\displaystyle h} можно применить принцип сжимающих отображений и решать данную систему методом простой итерации. В случае одной итерации это увеличивает вычислительные затраты всего лишь в два раза. {\displaystyle s}- число стадий. Это увеличивает вычислительные затраты, однако при достаточно малом {\displaystyle h} можно применить принцип сжимающих отображений и решать данную систему методом простой итерации. В случае одной итерации это увеличивает вычислительные затраты всего лишь в два раза.С другой стороны, Жан Кунцман (1961) и Джон Батчер (1964) показали, что при любом количестве стадий {\displaystyle s} существует неявный метод Рунге- Кутты с порядком точности  {\displaystyle p=2s}. Это значит, например, что для описанного выше явного четырёхстадийного метода четвёртого порядка существует неявный аналог с вдвое большим порядком точности. {\displaystyle p=2s}. Это значит, например, что для описанного выше явного четырёхстадийного метода четвёртого порядка существует неявный аналог с вдвое большим порядком точности.Неявные метод Рунге- Кутты второго порядка. Простейшим неявным методом Рунге- Кутты является модифицированный метод Эйлера «с пересчётом». Он задаётся формулой: 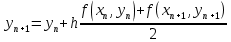 {\displaystyle {\mathbf {y} }_{n+1}={\mathbf {y} }_{n}+h{\frac {{\mathbf {f} }(x_{n},{\mathbf {y} }_{n})+{\mathbf {f} }(x_{n+1},{\mathbf {y} }_{n+1})}{2}}}Для его реализации на каждом шаге необходимы как минимум две итерации (и два вычисления функции). Прогноз: 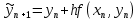 {\displaystyle {\tilde {\mathbf {y} }}_{n+1}={\mathbf {y} }_{n}+h{\mathbf {f} }(x_{n},{\mathbf {y} }_{n})}Коррекция: 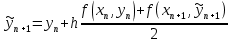 {\displaystyle {\mathbf {y}}_{n+1}={\mathbf {y}}_{n}+h{\frac {{\mathbf {f}}(x_{n},{\mathbf {y}}_{n})+{\mathbf {f}}(x_{n+1},{\tilde {\mathbf {y}}}_{n+1})}{2}}}Вторая формула- это простая итерация решения системы уравнений относительно 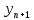 {\displaystyle {\mathbf {y}}_{n+1}}, записанной в форме сжимающего отображения. Для повышения точности итерацию-коррекцию можно сделать несколько раз, подставляя {\displaystyle {\mathbf {y}}_{n+1}}, записанной в форме сжимающего отображения. Для повышения точности итерацию-коррекцию можно сделать несколько раз, подставляя  {\displaystyle {\tilde {\mathbf {y}}}_{n+1}={\mathbf {y}}_{n+1}}. Модифицированный метод Эйлера «с пересчётом» имеет второй порядок точности. {\displaystyle {\tilde {\mathbf {y}}}_{n+1}={\mathbf {y}}_{n+1}}. Модифицированный метод Эйлера «с пересчётом» имеет второй порядок точности.Устойчивость. Преимуществом неявных методов Рунге- Кутты в сравнении с явными является их большая устойчивость, что особенно важно при решении жестких уравнений. Рассмотрим в качестве примера линейное уравнение 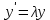 . Обычный метод Рунге- Кутты, применённый к этому уравнению, сведётся к итерации . Обычный метод Рунге- Кутты, применённый к этому уравнению, сведётся к итерации 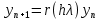 {\displaystyle y_{n+1}=r(h\lambda )\,y_{n}}, с {\displaystyle y_{n+1}=r(h\lambda )\,y_{n}}, с  , равным , равным 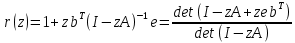 {\displaystyle r(z)=1+zb^{T}(I-zA)^{-1}e={\frac {\det(I-zA+zeb^{T})}{\det(I-zA)}},}где  {\displaystyle e} обозначает вектор-столбец из единиц. Функция {\displaystyle e} обозначает вектор-столбец из единиц. Функция  {\displaystyle r} называется функцией устойчивости. Из формулы видно, что {\displaystyle r} называется функцией устойчивости. Из формулы видно, что  {\displaystyle r} является отношением двух полиномов степени {\displaystyle r} является отношением двух полиномов степени  {\displaystyle s}, если метод имеет {\displaystyle s}, если метод имеет  {\displaystyle s} стадий. Явные методы имеют строго нижнюю треугольную матрицу {\displaystyle s} стадий. Явные методы имеют строго нижнюю треугольную матрицу 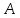 {\displaystyle A,} откуда следует, что {\displaystyle A,} откуда следует, что 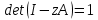 {\displaystyle \det(I-zA)=1,}и что функция устойчивости является многочленом. {\displaystyle \det(I-zA)=1,}и что функция устойчивости является многочленом. Численное решение данного примера дает чистый ноль при условии 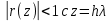 . {\displaystyle |r(z)|<1}{\displaystyle z=h\lambda }Множество таких . {\displaystyle |r(z)|<1}{\displaystyle z=h\lambda }Множество таких  {\displaystyle r} называется областью абсолютной устойчивости. В частности, метод называется A-устойчивым, если все {\displaystyle r} называется областью абсолютной устойчивости. В частности, метод называется A-устойчивым, если все  {\displaystyle r} с {\displaystyle r} с  {\displaystyle {\textrm {Re}}(z)<0} находятся в области абсолютной устойчивости. Функция устойчивости явного метода Рунге- Кутты является многочленом, поэтому явные методы Рунге- Кутты в принципе не могут быть A-устойчивыми. {\displaystyle {\textrm {Re}}(z)<0} находятся в области абсолютной устойчивости. Функция устойчивости явного метода Рунге- Кутты является многочленом, поэтому явные методы Рунге- Кутты в принципе не могут быть A-устойчивыми. Если метод имеет порядок 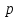 {\displaystyle p}, то функция устойчивости удовлетворяет условию {\displaystyle p}, то функция устойчивости удовлетворяет условию 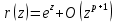 {\displaystyle r(z)={\textrm {e}}^{z}+O(z^{p+1})} при {\displaystyle r(z)={\textrm {e}}^{z}+O(z^{p+1})} при 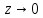 {\displaystyle z\to 0}. Таким образом, представляет интерес отношение многочленов данной степени, приближающее экспоненциальную функцию наилучшим образом. Эти отношения известны как аппроксимации Паде. Аппроксимация Паде с числителем степени {\displaystyle z\to 0}. Таким образом, представляет интерес отношение многочленов данной степени, приближающее экспоненциальную функцию наилучшим образом. Эти отношения известны как аппроксимации Паде. Аппроксимация Паде с числителем степени 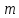 {\displaystyle m} и знаменателем степени {\displaystyle m} и знаменателем степени 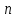 {\displaystyle n} А-устойчива тогда и только тогда, когда{\displaystyle m\leq n\leq m+2.} {\displaystyle n} А-устойчива тогда и только тогда, когда{\displaystyle m\leq n\leq m+2.}  {\displaystyle s}-стадийный метод Гаусса- Лежандра имеет порядок {\displaystyle s}-стадийный метод Гаусса- Лежандра имеет порядок 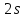 {\displaystyle 2s}, поэтому его функция устойчивости является приближением Паде {\displaystyle m=n=s}. Отсюда следует, что метод является A- устойчивым. Это показывает, что A-устойчивые методы Рунге- Кутты могут иметь сколь угодно высокий порядок. В отличие от этого, порядок А- устойчивости методов Адамса не может превышать два. {\displaystyle 2s}, поэтому его функция устойчивости является приближением Паде {\displaystyle m=n=s}. Отсюда следует, что метод является A- устойчивым. Это показывает, что A-устойчивые методы Рунге- Кутты могут иметь сколь угодно высокий порядок. В отличие от этого, порядок А- устойчивости методов Адамса не может превышать два.Решение интеграла дифференциального уравнения классическим методом Рунге- Кутты четвертого порядка. Вычислим классическим методом Рунге- Кутты четвертого порядка интеграл дифференциального уравнения 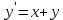 при при  , , 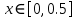 , ,  . .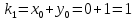 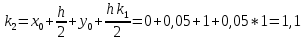 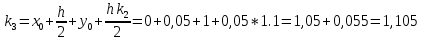 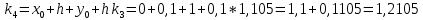 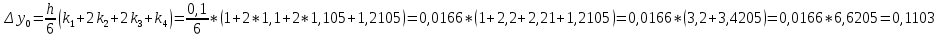 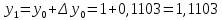  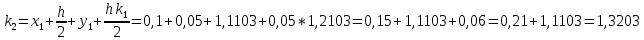  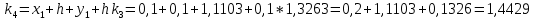  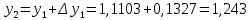 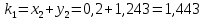 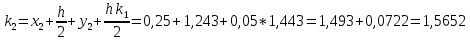 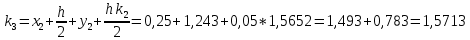 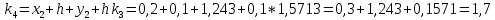  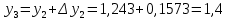  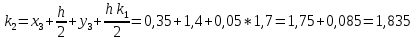 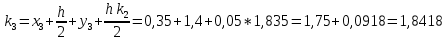 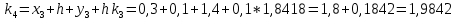 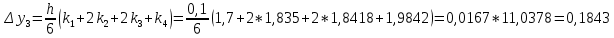 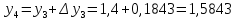 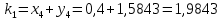 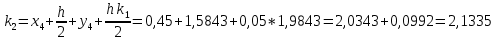 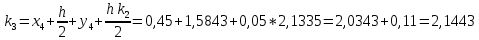 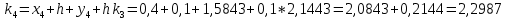  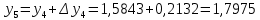  Произведем точное решение дифференциального уравнения: 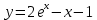 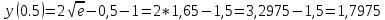 Полученные точное и численное значения совпали до пятого десятичного знака. Используемая литература. Ильина В.А., Силаев П.К. «Численные методы для физиков- теоретиков» часть 2, Москва- Ижевск: Институт компьютерных исследований, 2004год. |