математическое моделирование. 7915726_мат_мод_испр. Используя заданную функцию f(x), которая выбирается из таблицы 1 по числу N

• Название: Используя заданную функцию f(x), которая выбирается из таблицы 1 по числу N
• Анкор: математическое моделирование
• Дата: 29.01.2022
• Размер: 191.88 Kb.
• Имя файла: 7915726_мат_мод_испр.docx
• Тип: Документы; #345362
• страница: 3 из 5

Задание 4.

По заданной функции f(х) в заданном интервале рассчитать интеграл 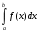заданным методом (интервал [а, b] разбить не менее чем на шесть подынтервалов). Метод численного интегрирования выбрать по числу N₄+1 из следующего общего списка методов:

1. Простейшие методы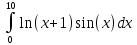



Формула левых прямоугольников

Абсолютная погрешность методов левых и правых прямоугольников оценивается как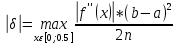


Найдем максимальное значение второй производной функции на интервале [0;10].


n = 2*(10-0)^2/(2*0,01) = 10000

n = 10000 – это n показывает, сколько нужно разбиений, чтобы достичь данным методом требуемой точности.

Ограничимся 20 интервалами

Формула прямоугольников основана на замене подынтегральной функции f(x) кусочно-постоянной функцией.
h = (10-0)/20 = 0,5

Расчеты приведем в таблице

х	f(x)
0	0
0,5	0,194
1	0,583
1,5	0,914
2	0,999
2,5	0,750
3	0,196
3,5	-0,528
4	-1,218
4,5	-1,666
5	-1,718
5,5	-1,321
6	-0,544
6,5	0,433
7	1,366
7,5	2,007
8	2,174
8,5	1,798
9	0,949
9,5	-0,177
10	-1,305
Сумма__23,768'>Сумма__5,192'>Сумма	5,192

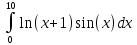= 5,195*0,5 = 2,596

Если разбить интервал на 100 интервалов, то получим (окончание таблицы)

9,4	0,058
9,5	-0,177
9,6	-0,412
9,7	-0,644
9,8	-0,872
9,9	-1,093
10	-1,305
Сумма	23,768

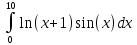= 23,768*0,1 = 2,377

|δ| =2*100/200 = 1

Если разбить интервал на 200 интервалов, то получим (окончание таблицы)

9,65	-0,528
9,7	-0,644
9,75	-0,759
9,8	-0,872
9,85	-0,984
9,9	-1,093
9,95	-1,200
10	-1,305
Сумма	46,910

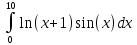= 46,910*0,05 = 2,345

|δ| =2*100/400 = 0,5
и т.д.

Для n=1000



|δ| =2*100/1000 = 0,2

Для n=1000



|δ| =2*100/10000 = 0,02

Для n=20000



|δ| =2*100/20000 = 0,01

Наверное, достаточно.

Значение интеграла, рассчитанное в MathCad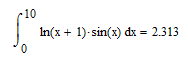