математическое моделирование. 7915726_мат_мод_испр. Используя заданную функцию f(x), которая выбирается из таблицы 1 по числу N
 Скачать 191.88 Kb. Скачать 191.88 Kb.
|
Задание 5.Задана система нелинейных уравнений: f1(x1,x2) = 0, f2(x1,x2) = 0 Уравнения системы выбираются изтаблицы № 2 в зависимости от числа N10. Требуется решить эту систему заданным в соответствии с номером варианта методом. Метод выбрать по числу N2+1 из следующего списка:  Метод Ньютона-Рафсона Метод Ньютона-Рафсонаcos(x2 -1) +x1 =0. cosx1 + x2 =1.5 Идея метода Ньютона для приближенного решения системы заключается в следующем: имея некоторое приближение x(k), мы находим следующее приближение x(k+1), аппроксимируя F(x(k+1)) линейным оператором и решая систему линейных алгебраических уравнений. Аппроксимируем нелинейную задачу F(x(k+1)) = 0 линейной F(x(k)) + J(x(k))(x(k+1) - x(k)) = 0 где J(x(k)) - матрица Якоби (якобиан) 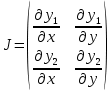 Для нашей системы 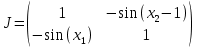 Построим графики и отделим корень графически, чтобы получить начальное приближение.
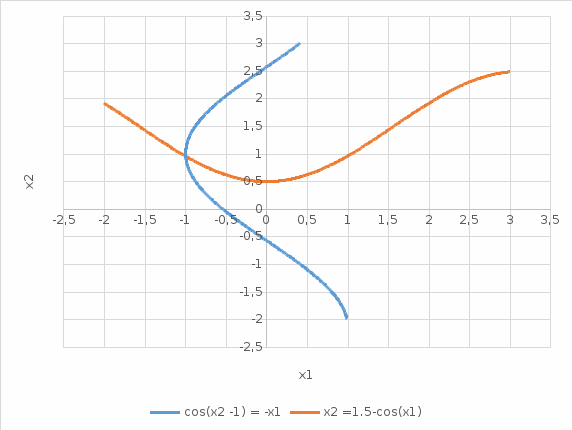 Линеаризованная система уравнений: 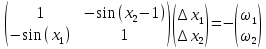 Реализуем алгоритм метода Ньютона-Рафсона: Первая итерация Начальные приближения 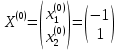 Невязки cos(1-1) - 1 = 0 cos(-1) + 1 – 1,5 = 0,040302
Матрица Якоби
Линеаризованная система уравнений: 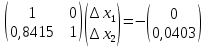 Δx1 = 0 0,8415Δx1 + Δx2 = -0,0403
1-е приближение неизвестных: 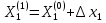 = -1+0 = -1 = -1+0 = -1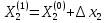 = 0,0403+1 = 0,9597 = 0,0403+1 = 0,9597
Корни уравнения х1 = -0,99916 х2 = 0,95899 Проверим в MathCad 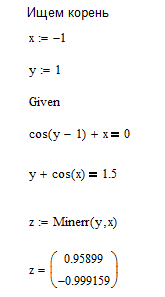 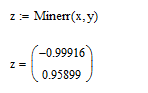 Функция Minerr использует тот же самый алгоритм, что и функция Find. Различие состоит в следующем. Если в результате поиска решения не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find, в отличие от функции Minerr, возвращает в этом случае сообщение об ошибке “решение не найдено”. Решения совпали. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
