АППРОКСИМАЦИЯ ФУНКЦИЙ. Аппроксимация функций
 Скачать 33.42 Kb. Скачать 33.42 Kb.
|
|
АППРОКСИМАЦИЯ ФУНКЦИЙ Математической моделью зависимости одной величины от другой является понятие функции y=f(x). Аппроксимацией называется получение некой функции, приближенно описывающей какую-то функциональную зависимость f(x), заданную таблицей значений, либо заданную в виде, неудобном для вычислений. При этом эту функцию выбирают такой, чтобы она была максимально удобной для последующих расчетов. Основной подход к решению этой задачи заключается в том, что функция fi(x) выбирается зависящей от нескольких свободных параметров c1, c2, …, cn, значения которых подбираются из некоторого условия близости f(x) и fi(x). Обоснование способов нахождения удачного вида функциональной зависимости и под- бора параметров составляет задачу теории аппроксимации функций. В зависимости от способа подбора параметров получают различные методы аппроксимации, среди которых наибольшее распространение получили интерполяция и среднеквадратичное приближение. Наиболее простой является линейная аппроксимация, при которой выбирают функцию линейно зависящую от параметров, т. е. в виде обобщенного многочлена: 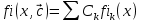 . Интерполяционным многочленомназывают алгебраический многочлен степени n-1, совпадающий с аппроксимируемой функцией в n выбранных точках. Погрешность аппроксимации функции f(x) интерполяционным многочленом степени n-1, построенным по n точкам, можно оценить, если известна ее производная порядка n. Суть среднеквадратичной аппроксимации заключается в том, что параметры функции . Интерполяционным многочленомназывают алгебраический многочлен степени n-1, совпадающий с аппроксимируемой функцией в n выбранных точках. Погрешность аппроксимации функции f(x) интерполяционным многочленом степени n-1, построенным по n точкам, можно оценить, если известна ее производная порядка n. Суть среднеквадратичной аппроксимации заключается в том, что параметры функции 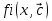 подбираются такими, чтобы обеспечить минимум квадрата расстояния между функциями f(x) и fi(x, c). Метод наименьших квадратов является частным случаем среднеквадратичной аппроксимации. При использовании метода наименьших квадратов аналогично задаче интерполяции в области значений x, представляющей некоторый интервал [a, b], где функции f(x) и fi(x) должны быть близки, выбирают систему различных точек (узлов) x1, ..., xm, число которых больше, чем количество искомых параметров. Далее, требуют чтобы сумма квадратов невязок во всех узлах была минимальна. подбираются такими, чтобы обеспечить минимум квадрата расстояния между функциями f(x) и fi(x, c). Метод наименьших квадратов является частным случаем среднеквадратичной аппроксимации. При использовании метода наименьших квадратов аналогично задаче интерполяции в области значений x, представляющей некоторый интервал [a, b], где функции f(x) и fi(x) должны быть близки, выбирают систему различных точек (узлов) x1, ..., xm, число которых больше, чем количество искомых параметров. Далее, требуют чтобы сумма квадратов невязок во всех узлах была минимальна.Интерполяция общего вида Следует отметить, что ввиду громоздкости многочлены Ньютона и Лагранжа уступают по эффективности расчета многочлену общего вида. Поэтому, когда требуется производить многократные вычисления многочлена, построенного по одной таблице, оказывается выгодно вначале один раз найти коэффициенты с. Коэффициенты находят прямым решением системы с, затем вычисляют его значения по алгоритму Горнера. Недостатком такого вида аппроксимации является необходимость решения системы линейных алгебраических уравнений. Интерполяционный многочлен Лагранжа Лагранжем была предложена своя форма записи общего интерполяционного алгебраического многочлена в виде, не требующем решения системы линейных алгебраических уравнений. Следует отметить, что ввиду громоздкости многочлены Ньютона и Лагранжа уступают по эффективности расчета многочлену общего вида. Интерполяционный многочлен Ньютона Ньютоном была предложена форма записи общего интерполяционного алгебраического многочлена в виде, не требующем решения системы линейных алгебраических уравнений. Следует отметить, что ввиду громоздкости многочлены Ньютона и Лагранжа уступают по эффективности расчета многочлену общего вида. Линейная и квадратичная интерполяции Иногда при интерполяции по заданной таблице при m>3 точек приме- няют квадратичную (n=3) или линейную (n=2) интерполяцию. В этом случае для приближенного вычисления значения функции f(x) в текущей точке xТ находят в таблице ближайшие к этой точке (i-1), i, (i+1)-й узлы из общей таблицы, строят интерполяционный многочлен Ньютона первой или второй степени по формулам. Формулы численного интегрирования Формулы для вычисления интеграла получают следующим образом. Область интегрирования [a, b] разбивают на m малых отрезков с шагом h=b-a/m. Значение интеграла по всей области равно сумме интегралов на отрезках. Выбирают на каждом отрезке 1 – 5 узлов и строят для каждого отрезка интерполяционный многочлен соответствующего порядка. Вычисляют интеграл от этого многочлена на отрезке. В результате получают выражение интеграла (формулу численного интегрирования) через значения подынтегральной функции в выбранной системе точек. Такие выражения называют квадратурными формулами. Формула средних Формула средних получается, если на каждом i-ом отрезке [xi-1, xi] взять один центральный узел xi-1/2 = xi - h/2, соответствующий середине отрезка. Функция на каждом отрезке аппроксимируется многочленом нулевой степени (константой) P0(x) = f(xi-1/2). Погрешность формулы средних имеет второй порядок по h. 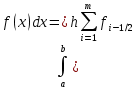 . .Формула трапеций Формула трапеций получается при аппроксимации функции f(x) на каждом отрезке интерполяционным многочленом первого порядка, т. е. прямой, проходящей через точки x(i-1) f(i-1), x(i) f(i). Площадь криволинейной фигуры заменяется площадью трапеции с высотами f(i-1) f(i)и основанием h. Погрешность формулы трапеций в два раза больше, чем погрешность формулы средних. 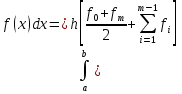 Формула Симпсона Формула Симпсона получается при аппроксимации функции f(x) на каждом отрезкеинтерполяционным многочленом второго порядка (параболой) c узлами x(i-1), x(i-1/2), x(i). Погрешность формулы Симпсона имеет четвертый порядок по h. 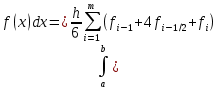 . .Формулы Гаусса При построении предыдущих формул в качестве узлов интерполяционного многочлена выбирались середины или концы интервала разбиения. При этом оказывается, что увеличение количества узлов не всегда приводит к уменьшению погрешности. Суть методов Гаусса с n узлами состоит в таком расположении этих n узлов интерполяционного многочлена на отрезке x(i-1), x(i), при котором достигается минимум погрешности квадратурной формулы. Детальный анализ показывает, что узлами, удовлетворяющими такому условию, являются нули ортогональнoго многочлена Лежандра n-й степени. Для n=2 узлы на отрезке x(i-1), x(i)должны быть выбраны следующим образом: 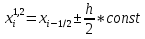 . И соответствующая формула Гаусса с двумя узлами имеет вид: . И соответствующая формула Гаусса с двумя узлами имеет вид: 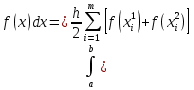 . Порядок погрешности этой формулы 4-ый. Для n=3 узлы выбираются следующим образом: . Порядок погрешности этой формулы 4-ый. Для n=3 узлы выбираются следующим образом: 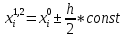 . и соответствующая формула Гаусса с тремя узлами имеет вид: . и соответствующая формула Гаусса с тремя узлами имеет вид: 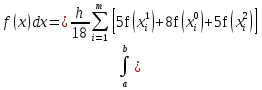 . Порядок погрешности этой формулы шестой. особенно широко применяются для вычисления несобственных интегралов специального вида, когда подынтегральная функция имеет достаточно высокие производные. . Порядок погрешности этой формулы шестой. особенно широко применяются для вычисления несобственных интегралов специального вида, когда подынтегральная функция имеет достаточно высокие производные.Задачи для обыкновенных дифференциальных уравнений Обыкновенные дифференциальные уравнения или системы таких уравнений часто используются для построения математических моделей динамических процессов, т. е. процессов перехода физических систем из одного со- стояния в другое, бесконечно близкое. Однако классы решений, для которых разработаны точные решения, довольно узки и охватывают только малую часть возникающих на практике задач. В силу этого важное значение имеют приближенные численные методы решения, ориентированные на широкий класс встречающихся на практике дифференциальных уравнений. Известно, что заменой переменных дифференциальное уравнение n-го порядка всегда может быть сведено к эквивалентной системе n дифференциальных уравнений 1-го порядка. Среди таких систем выделим класс систем, разрешенных относительно производной неизвестных функций. Обычно требуется найти решение системы для значений x из заданного интервала. для выделения одного нужного решения, надо наложить дополнительно m условий на функции. В зависимости от способа постановки дополнительных условий можно выделить два основных типа задач/ краевая (граничная) задача, когда часть условий задается на границе a (при x=a), остальные условия – на границе b (при x=b). Обычно это значения искомых функций на границах; задача Коши (задача с начальными условиями), когда все условия заданы в начале отрезка в виде 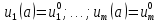 . . ОСНОВНАЯ Ф_ЛА 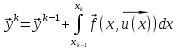 Основные положения метода сеток для решения задачи Коши Чаще всего задача Коши решается методом сеток. Суть метода сеток состоит в следующем. В области интегрирования выбирается упорядоченная система точек называемая сеткой. Точки называют узлами, а h – шагом сетки. Если h=b-a/2, сетка называется равномерной. Также существует неравномерная сетка. Решение ищется в виде таблицы значений в узлах выбранной сетки, для чего дифференциальное уравнение заменяется системой алгебраических уравнений, связывающих между собой значения искомой функции в соседних узлах. Такая система называется конечно-разностной схемой (интегро-интерполяционный метод). Согласно этому методу для получения конечно-разностной схемы проинтегрируем дифференциальное уравнение на каждом интервале для k=1,2,...,n. получаем, что значение искомой функции в к-ом узле определяется через значение в предшествующем узле с поправкой, выраженной в форме интеграла. Аппроксимируя интеграл одной из квадратурных формул, получаем те или иные формулы относительно приближенных неизвестных значений искомой функции. Структура конечно-разностной схемы для задачи Коши такова, что она устанавливает закон рекуррентной последовательности для искомого решения. При замене интеграла приближенной квадратурной формулой вносится погрешность аппроксимации дифференциального уравнения разностным. Таким образом, если имеется аппроксимация и схема устойчива, то, выбрав достаточно малый шаг h, можно получить решение с заданной точностью при этом затраты на вычисления резко уменьшаются с увеличени- ем порядка аппроксимации p. Явная схема 1-го порядка (метод Эйлера) Вычисляя интеграл в (23.4) по формуле левых прямоугольников получим: 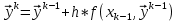 . Погрешность аппроксимации psi(h) и соответственно точность ε(h) имеют первый порядок в силу того, что формула левых прямоугольников на интервале имеет погрешность первого порядка, а схема устойчива. . Погрешность аппроксимации psi(h) и соответственно точность ε(h) имеют первый порядок в силу того, что формула левых прямоугольников на интервале имеет погрешность первого порядка, а схема устойчива.Неявная схема 1-го порядка Вычисляя интеграл по формуле правых прямоугольников получим 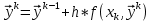 . Эта схема явно не разрешена относительно . Эта схема явно не разрешена относительно 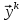 , поэтому для получения , поэтому для получения 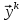 требуется использовать итерационную процедуру решения уравнения. За начальное приближение можно взять значение из предыдущего узла. Обычно, если h выбрано удачно, достаточно сделать 2 – 3 итерации для достижения заданной погрешности . Эффективность неявной схемы заключается в том, что у нее константа устойчивости С0 значительно меньше, чем у явной схемы. требуется использовать итерационную процедуру решения уравнения. За начальное приближение можно взять значение из предыдущего узла. Обычно, если h выбрано удачно, достаточно сделать 2 – 3 итерации для достижения заданной погрешности . Эффективность неявной схемы заключается в том, что у нее константа устойчивости С0 значительно меньше, чем у явной схемы.Неявная схема 2-го порядка Вычисляя интеграл по формуле трапеций. Так как формула трапеций имеет второй порядок точности, то и погрешность метода имеет второй порядок. Схема явно не разрешена относительно, поэтому требуется итерационная процедура. Обычно, если h выбрано удачно, достаточно сделать 2 – 3 итерации для достижения заданной погрешности . Эффективность неявной схемы заключается в том, что у нее константа устойчивости С0 значительно меньше, чем у явной схемы. Схема Рунге – Кутта 2-го порядка Вычисляя интеграл по формуле средних прямоугольников. Уравнение разрешено явно, однако в правой части присутствует неизвестное значение в середине отрезка. Для решения этого уравнения используют следующий способ. Вначале по явной схеме рассчитывают предиктор. После этого рассчитывают корректор. В результате схема оказывается явной и имеет второй порядок. Схема Рунге – Кутта 4-го порядка Вычисляя интеграл по формуле Симпсона. Ввиду того, что формула Симпсона имеет четвертый порядок, погрешность метода тоже имеет четвертый порядок. Можно по-разному реализовать расчет неявного уравнения, однако наибольшее распространение получил следующий способ. Вычисляют предиктор по формулам, затем корректор. Многошаговые схемы Адамса При построении всех предыдущих схем для вычисления интеграла в правой части использовались лишь точки в диапазоне одного шага. Поэтому при реализации таких схем для вычисления следующего значения требуется знать только одно предыдущее значение. Такие схемы называют одношаговыми. Идея методов Адамса заключается в том, чтобы для повышения точности использовать уже вычисленные на предыдущих шагах значения в нескольких предыдущих узлах. Явная экстраполяционная схема Адамса 2-го порядка Заменив подынтегральную функцию интерполяционным многочленом Ньютона получим новую формулу. Схема двухшаговая, поэтому для начала расчетов необходимо, сделав один шаг, найти по методу Рунге – Кутта 2-го порядка 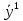 , после чего вычислять оставшиеся значения. , после чего вычислять оставшиеся значения.Явная экстраполяционная схема Адамса 3-го порядка Заменив подынтегральную функцию интерполяционным многочленом Ньютона получим формулу. Схема трехшаговая, поэтому для начала расчетов необходимо, сделав два шага, найти по методу Рунге – Кутта 4-го порядка 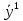 , , 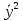 , после чего вычислить оставшиеся значения. , после чего вычислить оставшиеся значения.Неявная схема Адамса 3-го порядка Заменив подынтегральную функцию интерполяционным многочленом Ньютона получим формулу. Так как схема двухшаговая, то для начала расчетов необходимо, сделав один шаг, найти y(1) по методу Рунге – Кутта 4-го порядка, после чего y2, y3, ... вычисляются. Эта формула явно не разрешена относительно y(k), поэтому для получения y(k) требуется использовать итерационную процедуру решения уравнения. Значение y(k,0)следует рассчитать по формуле. Краевая (граничная) задача Рассмотрим граничную задачу для линейного дифференциального уравнения второго порядка с переменными коэффициентами y//+p(x) y/ + q(x) y = f(x) на отрезке [a, b] с граничными условиями общего вида. В тех случаях, когда невозможно получить решение этой задачи аналитическим методом, используются приближенные или численные методы. Суть приближенных методов. Выбирается система линейно-независимых дважды дифференцируемых функций, при этом функция должна удовлетворять граничным условиям, Искомое решение представляется в виде линейной комбинации базисных функций. Метод стрельбы Сущность метода стрельбы заключается в сведении решения граничной задачи к многократному решению задачи Коши. Введя замену переменных y1(x)=dy/dx, заменим дифференциальное уравнение второго порядка системой двух дифференциальных уравнений первого порядка: dy/dx = y1, dy1/dx = f(x) – p(x)y1 – q(x)y с граничными условиями общего вида. Задавшись произвольным начальным условием для y(x) из первого уравнения получаем начальное условие для y1(x): y1(a)=(A-1 y0)/1 Система уравнений представляет собой задачу Коши, которая решается одним из ранее рассмотренных методов. Получив в результате решения задачи Коши значения y(b), y1(b) на правом конце отрезка [a, b], проверяют, выполнилось ли второе условие, которое может быть представлено в виде F(y0)=2 y(b)+2 y1(b)–B=0. Таким образом граничная задача в итоге сводится к нахождению корня уравнения F(y0)=0 для вычисления правой части которого необходимо решить задачу Коши. Описанный алгоритм называется методом стрельбы, поскольку в нем как бы проводится «пристрелка» по углу наклона интегральной кривой в начальной точке. Метод конечных разностей Сущность метода в том, что он сводит решение граничной задачи для дифференциального уравнения к решению системы линейных алгебраических уравнений относительно значений искомой функции на заданном множестве точек. Это достигается путем замены производных, входящих в дифференциальное уравнение их конечно – разностными аппроксимациями. Граничные условия также должны представляться в разностном виде путем аппроксимации производных y/(a), y/(b) помощью конечно-разностных соотношений. предпочтительнее аппроксимировать первые производные со вторым порядком точности. В итоге полученные выражения образуют систему линейных алгебраических уравнений (n+1)-го порядка, решив которую, получают решение граничной задачи в виде значений искомой функции y(x) в узловых точках. |
