Практикум. Тема Интегральное исчисление функции одной переменной
 Скачать 125.52 Kb. Скачать 125.52 Kb.
|
Тема 6. Интегральное исчисление функции одной переменнойОсновные понятия. Первообразная. Неопределенный интеграл. Основные методы интегрирования. Определенный интеграл. Приложения определенного интеграла. Вопросы, вынесенные на самостоятельное изучение Интегрирование некоторых иррациональностей. Интегралы, не выражающиеся через элементарные функции. Приближенное вычисление определенных интегралов. Вопросы для подготовки к семинару Что называется неопределенным интегралом функции f(х)? Сформулируйте и докажите основные свойства неопределенного интеграла. Напишите формулу замены переменной в неопределенном интеграле. Напишите формулу подстановки в неопределенном интеграле. Напишите на память таблицу неопределенных интегралов и сверьте вашу таблицу c таблицей в пособии. Добейтесь полного их совпадения, после чего рекомендуем приступать к отысканию неопределенных интегралов. Какие вы знаете методы интегрирования и в чем заключается идея этих методов? В чем заключается различие метода замены переменной от метода подстановки? Как вы понимаете выражение «неберущиеся интегралы»? Каким условиям должна удовлетворять подынтегральная функция, чтобы существовал неопределенный интеграл (или первообразная)? Напишите формулу интегрирования по частям для неопределенного интеграла. Какие дроби называются простейшими рациональными дробями и чему равны интегралы от таких функций? В чем отличие определенного интеграла от неопределенного? Чему равен определенный интеграл, если пределы интегрирования – фиксированные действительные числа? Каким условиям должна удовлетворять подынтегральная функция, чтобы определенный интеграл от нее существовал? Какова связь между определенным и неопределенным интегралами? Числом или функцией будет определенный интеграл с переменными пределами интегрирования? По какой формуле вычисляется определенный интеграл? Напишите формулу замены переменной в определенном интеграле. Напишите формулу интегрирования по частям определенного интеграла. Как с помощью определенного интеграла вычисляются площади плоских фигур? Как с помощью определенного интеграла вычисляются объемы по площадям перпендикулярных сечений, объемы тел вращения? ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 1. Найдите неопределенные интегралы: 1) 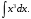 2) 2) 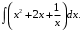 3) 3) 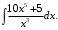 4) 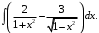 5) 5) 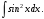 6) 6) 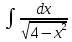 7) 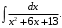 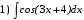 ; ; 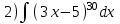 ; ; 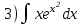 ; 8) ; 8) 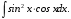 9) 9) 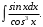 10) 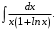 10) 10) 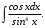 2. Применяя метод интегрирования по частям, найдите следующие интегралы: 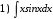 ; ; 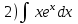 ; ; 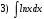 ; ; 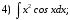 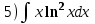 ; ;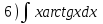 ; ;  ; ; 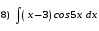 ; ; 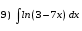 ; ;3. Найдите интегралы от рациональных дробей: 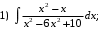 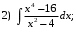 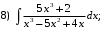 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 1. Вычислить интегралы, пользуясь формулой Ньютон – Лейбница. 1) 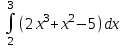 ; 2) ; 2) 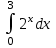 ; 3) ; 3) 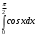 ; 4) ; 4) 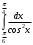 ; ;2. Интегрированием по частям вычислить следующие определенные интегралы: 1) 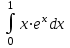 ; 2) ; 2) 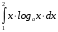 ; 3) ; 3) 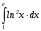 ; ;4) 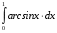 ; 5) ; 5) 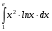 ; 6) ; 6) 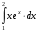 . .ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 1. Вычислите площадь фигуры, ограниченной линиями: 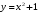 , , 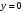 , , 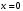 , , 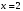 . .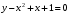 , , 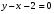 . .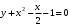 , , 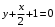 . .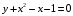 , , 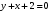 . .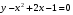 , , 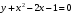 . .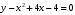 , , 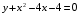 . .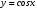 , , 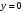 , , 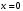 , , 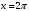 . .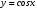 , , 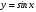 , , 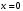 , , 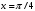 . .2. Вычислите объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями: 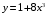 , , 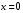 , , 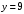 . .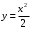 , , 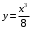 . .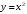 , , 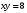 , , 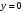 , , 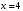 . .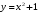 , , 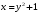 , , 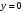 , , 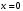 , , 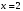 . .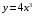 , , 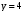 , , 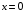 . .3. Найдите длины дуг следующих линий: 1) 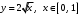 . 2) . 2) 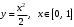 . .3) 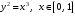 . 4) . 4) 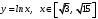 . . |
