архимед. Архимедова сила
 Скачать 119.72 Kb. Скачать 119.72 Kb.
|
Тема: Архимедова сила. Цель: Узнать кто такой Архимед? Узнать , как вычисляется Архимедова сила. Решить 3 задачи на вычисление. Архимед был одним из самых замечательных ученых Древней Греции. Наверное, вы слышали легенду о том, как был открыт один из законов физики. Однажды, погрузившись в ванну в купальне, Архимед заметил, что своим телом он вытеснил часть воды и она выплеснулась, а при этом вода его как бы поддерживала. Ученый сразу понял, что здесь и заключается решение мучавшей его проблемы. С криком "Эврика!" (Нашел!") он выскочил из купальни и помчался по улице: ему не терпелось сделать вычисления. Так был открыт знаменитый закон выталкивающей силы. Этот человек соорудил невиданные до той поры метательные военные машины для обороны города Сиракузы на острове Сицилия (где он родился и жил), которые сеяли панику и ужас в рядах римских легионеров и обращали их в бегство. Придумал он и способ поджигать вражеские корабли — с помощью тысячи больших зеркал, которые держали в руках воины осажденного города. Этими зеркалами солнечные зайчики были сфокусированы в единый луч, который и воспламенил суда неприятеля. Параллелограмм сил или скоростей, о котором говорят на уроках физики, также изобретение Архимеда. Теория простых механизмов, разработанная великим ученым, привела к развитию важных разделов механики. Винт Архимеда применяется в различных машинах, служит для подъема сыпучих грузов, перемещает детали на заводах. Огромный (по тем временам) корабль "Сиракосия" был спущен на воду с помощью системы блоков, которой управлял один воин. Архимедово правило рычага и сейчас называют иногда золотым правилом механики. И именно ему легенда приписывает слова: "Дайте мне точку опоры, и я переверну мир!" Несколько менее известно, что Архимед был не только замечательным механиком и физиком, но и гениальным математиком. Что же сделал он в этой области знания, какие его мысли и теории вошли сегодня в золотой фонд науки? Здесь прежде всего нужно сказать о вычислении длин. Известно, что длина окружности с радиусом R равна 2? где R — некоторое число, несколько больше чем 3. Это видно из рассмотрения правильного вписанного шестиугольника: его периметр равен 6R, а длина окружности чуть больше! Как же поточнее вычислить значение ?? Именно Архимед в своем изящном исследовании, связанном с рассмотрением вписанных и описанных многоугольников, дал замечательную для своего времени оценку числа л. Он установил, что это число заключено между 3 10/71 и 3 1/7 . Вооружитесь микрокалькулятором, и вы легко обнаружите, что эти числа записываются в виде 3,140845 и 3,142857. Таким образом, Архимедом было найдено приближенное значение ? ˜ 3,14, которым мы и сейчас пользуемся для расчетов с не очень большой точностью. Замечательно и другое открытие Архимеда, также связанное с измерением длин. Вам нужно по возможности точно измерить длину скамейки. Вы сначала определяете, сколько раз в скамейке откладывается метр; если имеется остаток — узнаете, сколько в нем дециметров; если снова есть остаток — находите, сколько в нем сантиметров, миллиметров. Такой процесс измерения был логически исследован Архимедом, который в связи с этим сформулировал аксиому, и сейчас называемую аксиомой Архимеда. Она состоит в том, что, взяв какой-либо отрезок (единицу измерения) и откладывая его на другом отрезке (каким бы большим он ни был), мы после некоторого числа откладываний обязательно дойдем до конца измеряемого отрезка и "перескочим" через его конец. Не правда ли, это настолько очевидно, кажется, незачем и говорить об этом пустяке? Но удивительное дело! Именно аксиома Архимеда сейчас особенно волнует умы ученых. Мы все чаще говорим то, что Архимед сумел в седой древности вычленить и сформулировать именно такую аксиому, которая сегодня важна и актуальна, свидетельствует о большой его проницательности и научном предвидении. Еще одно открытие Архимеда связано с измерением площадь. Решая задачу, как построить отрезок, длина которого равна длине окружности данного круга, ученый вычислил отношение длины окружности к диаметру и нашел, что оно заключено 3 10/71 и 3 1/7. Созданный им метод вычисления длины окружности и площади фигуры, с помощью которого он получил результат, предвосхищает идеи особого интегрального исчисления, открытого (спустя два тысячелетия после Архимеда!) двумя другими гениями — И. Ньютоном и Г. В. Лейбницем. Именно Ньютон, который хорошо знал работы Архимеда и опирался на них, объяснял свои научные успехи тем, что "стоял на плечах гигантов". Много важных открытий имеется в научном наследии Архимеда. Он установил теорему о том, что три медианы треугольника пересекаются в одной точке; нашел замечательные свойства кривой, которую теперь называют спиралью Архимеда; вычислил объем шара; создал формулу суммы убывающей геометрической прогрессии. Существует предание, что римский воин завоеватель наступил ногой на чертежи, которые Архимед делал на влажном песке. "Не смей трогать мои чертежи!" — воскликнул ученый. Римскому воину было невдомек, что перед ним гений, слава которого переживет тысячелетия. Он пронзил ученого мечом. Обливаясь кровью, упал Архимед на свои чертежи, возможно заключавшие новое открытие. Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа. Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа. 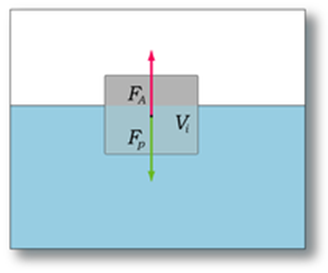 ρж g Vж = ρт g Vт Плавание тел — состояние равновесия твердого тела, частично или полностью погруженного в жидкость (или газ). Основная задача теории плавания тел — определение равновесия тела, погруженного в жидкость, выяснение условий устойчивости равновесия. На простейшие условия плавания тел указывает закон Архимеда. Рассмотрим эти условия. Как известно, на все тела, погруженные в жидкость, действует сила Архимеда Fа(выталкивающая сила), направленная вертикально вверх, однако всплывают далеко не все. Чтобы понять, почему одни тела всплывают, а другие тонут, необходимо учесть еще одну силу, действующую на все тела, — силу тяжести Fт которая направлена вертикально вниз, т. е. противоположно FA. Если тело оставить внутри жидкости в состоянии покоя, то оно начнет двигаться в сторону, в которую направлена большая из сил. При этом возможны следующие случаи: 1. если архимедова сила меньше силы тяжести (FA< Fт), то тело опустится на дно, т. е. утонет (рис. а); 2. если архимедова сила больше силы тяжести (FA> Fт), то тело всплывет (рис. б); 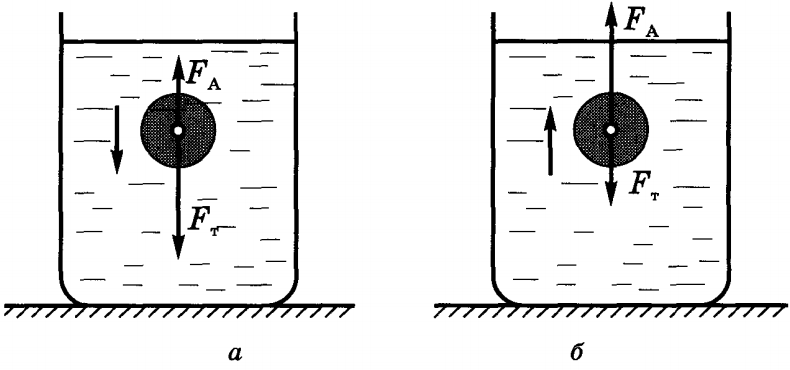 3) если архимедова сила равна силе тяжести (FA = Fт), то тело останется в покое. Последнее условие является условием равновесия тела в жидкости: FA = Fт. Равенство FA = Fт выражает условие плавания тел: для того, чтобы тело плавало, необходимо, чтобы действующая на него сила тяжести уравновешивалась архимедовой (выталкивающей) силой. Условию плавания тел можно придать другую форму. Представим архимедову силу в виде: FA = ρж Vж g, где ρж — плотность жидкости, Vm — объем жидкости, вытесненный телом, g — ускорение свободного падения. Силу тяжести, действующую на тело, тоже можно выразить через объем V и плотность тела ρ: Fт = mg = ρVg, де т — масса тела. Подставим выражения FA = ρж Vж g и Fт = mg = ρVg в равенство FA = Fт: ρVg = ρж Vж g. Разделив обе части этого равенства на g , получим условие плавание тел в новой форме: ρV = ρж Vж. Из полученного соотношения можно вывести два важных следствия. 1. Для того чтобы тело плавало, будучи полностью погруженным в жидкость, необходимо, чтобы плотность тела была равна плотности жидкости. 2. Для того чтобы тело плавало, частично выступая над поверхностью жидкости, необходимо, чтобы плотность тела была меньше плотности жидкости. При ρ > ρж плавание тел невозможно, так как в этом случае сила тяжести превышает архимедову силу, и тело тонет.  Что будет происходить с телом, у которого ρ < ρж, если его полностью погрузить в жидкость? В этом случае архимедова сила будет преобладать над силой тяжести, и потому тело начнет подниматься вверх. Пока тело будет двигаться, оставаясь полностью погруженным в жидкость, архимедова сила будет оставаться неизменной. Но как только тело достигнет поверхности жидкости и появится над ней, эта сила (по мере уменьшения объема части тела, погруженного в жидкость) будет становиться все меньше и меньше. Всплытие прекратится тогда, когда архимедова (выталкивающая) сила станет равной силе тяжести. При этом чем меньшей плотностью (по сравнению с плотностью жидкости) обладает тело, тем меньшая его часть останется внутри жидкости. Плавание судов . Масса современных судов достигает нескольких десятков тысяч тонн. Почему же они не тонут? Дело в том, что, несмотря на огромную массу, их средняя плотность по-прежнему меньше плотности воды (благодаря тому, что в кораблях много пустых помещений). При этом сила тяжести, действующая на судно, уравновешивается архимедовой (выталкивающей) силой, и судно плавает. Глубина, на которую плавающее судно погружается в воду, называется осадкой судна. При полной загрузке судна оно не должно погружаться в воду ниже так называемой грузовой ватер -линии. Вес воды, вытесняемый судном при погружении до ватерлинии, равный силе тяжести, действующей на судно с грузом, называется водоизмещением судна. Если из водоизмещения вычесть вес самого судна, получим грузоподъемность судна. Грузоподъемность показывает вес груза, перевозимого судном. Воздухоплавание. На все тела в воздухе (как и в жидкости) действует выталкивающая (архимедова) сила. Для тел, находящихся в воздухе, она равна: FA = ρвозд V g, где ρвозд — плотность воздуха. Если эта сила окажется больше силы тяжести, действующей на тело, то тело взлетит. На этом основано воздухоплавание. Летательные аппараты, применяемые в воздухоплавании, называют аэростатами (от греч. aer — воздух, status — стоящий). Неуправляемые аэростаты свободного полета с оболочкой, имеющей форму шара, называют воздушными шарами. Для исследования верхних слоев атмосферы (стратосферы) еще не так давно применялись огромные воздушные шары — стратостаты. Управляемые аэростаты (имеющие двигатель и воздушные винты) называют дирижаблями. Воздушный шар не только сам поднимается вверх, но может поднять и некоторый груз: кабину, людей, приборы. Для того, чтобы определить, какой груз способен поднять воздушный тар, следует знать его подъемную силу. Подъемная сила воздушного шара равна разности между архимедовой силой и действующей на шар силой тяжести: F = FA - Fт. Чем меньше плотность газа, наполняющего воздушный шар данного объема, тем меньше действующая на него сила тяжести и тем больше возникающая подъемная сила. Воздушные шары можно наполнять гелием, водородом или нагретым воздухом. Хотя у водорода меньше плотность, чем у гелия, все же чаще в целях безопасности применяют гелий (водород — горючий газ). Гораздо проще осуществить подъем и спуск шара, наполненного горячим воздухом. Для этого под отверстием, находящимся в нижней части шара, располагают горелку. Она позволяет регулировать температуру воздуха, а значит, и его плотность и подъемную силу. Можно подобрать такую температуру шара, при которой вес шара и кабины будет равен выталкивающей силе. Тогда шар повиснет в воздухе, и с него будет легко проводить наблюдения. Вывод: Мы узнали , что такое сила Архимеда. Научились вычислять силу Архимеда. |
