Формулы. Арифметическая прогрессия к оглавлению

• Название: Арифметическая прогрессия к оглавлению
• Анкор: Формулы
• Дата: 02.03.2021
• Размер: 1.09 Mb.
• Имя файла: Формулы.docx
• Тип: Документы; #180943

Арифметическая прогрессия

К оглавлению…

Формулы n-го члена арифметической прогрессии:





Соотношение между тремя соседними членами арифметической прогрессии:



Формула суммы арифметической прогрессии:



Свойство арифметической прогрессии:



Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:





Соотношение между тремя соседними членами геометрической прогрессии:



Формула суммы геометрической прогрессии: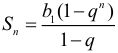



Формула суммы бесконечно убывающей геометрической прогрессии: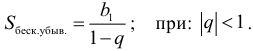



Свойство геометрической прогрессии:



Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник: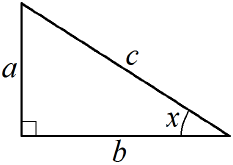



Тогда, определение синуса:



Определение косинуса:



Определение тангенса:



Определение котангенса: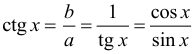



Основное тригонометрическое тождество:



Простейшие следствия из основного тригонометрического тождества:





Формулы двойного угла

Синус двойного угла: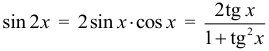



Косинус двойного угла: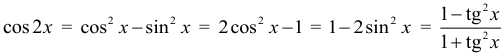



Тангенс двойного угла: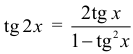



Котангенс двойного угла: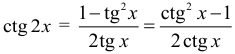



Тригонометрические формулы сложения

Синус суммы:



Синус разности:



Косинус суммы:



Косинус разности:



Тангенс суммы: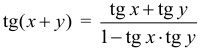



Тангенс разности: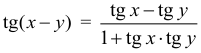



Котангенс суммы: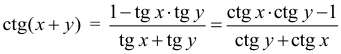



Котангенс разности: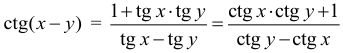



Тригонометрические формулы преобразования суммы в произведение

Сумма синусов: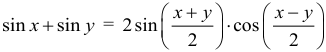



Разность синусов: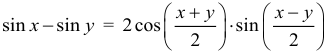



Сумма косинусов: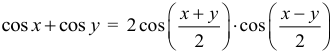



Разность косинусов: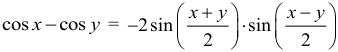



Сумма тангенсов: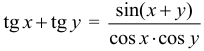



Разность тангенсов: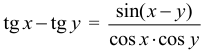



Сумма котангенсов: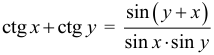



Разность котангенсов: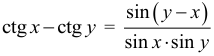



Тригонометрические формулы преобразования произведения в сумму

Произведение синусов:



Произведение синуса и косинуса:



Произведение косинусов:



Формулы понижения степени

Формула понижения степени для синуса:



Формула понижения степени для косинуса:



Формула понижения степени для тангенса:



Формула понижения степени для котангенса:



Формулы половинного угла

Формула половинного угла для тангенса:



Формула половинного угла для котангенса:



Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы: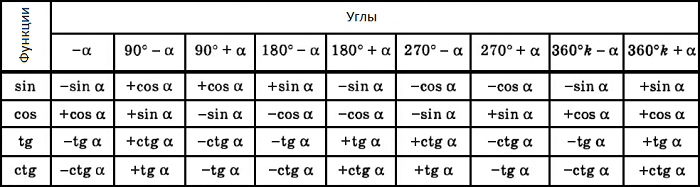



Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций: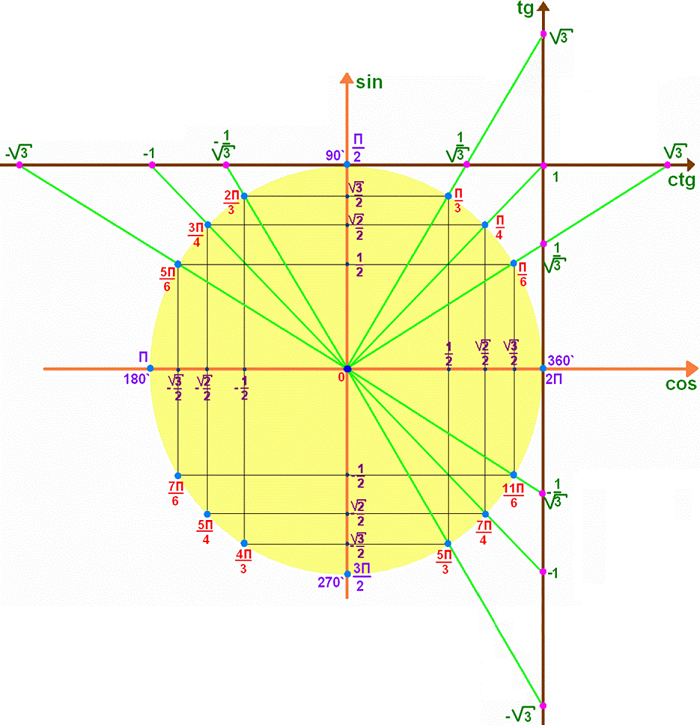



Тригонометрические уравнения

К оглавлению…

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения: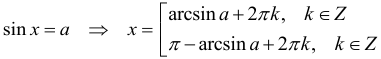





Для остальных тригонометрических функций запись однозначна. Для косинуса:



Для тангенса:



Для котангенса:



Решение тригонометрических уравнений в некоторых частных случаях:

















Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник: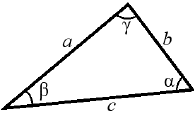



Тогда, сумма углов треугольника:



Площадь треугольника через две стороны и угол между ними:



Площадь треугольника через сторону и высоту опущенную на неё:



Полупериметр треугольника находится по следующей формуле:



Формула Герона для площади треугольника:



Площадь треугольника через радиус описанной окружности:



Формула медианы: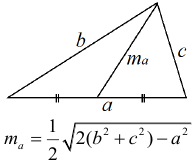



Свойство биссектрисы: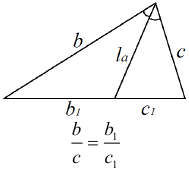



Формулы биссектрисы: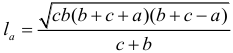





Основное свойство высот треугольника:



Формула высоты: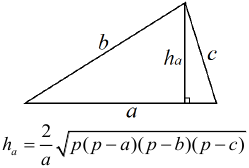



Еще одно полезное свойство высот треугольника: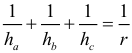



Теорема косинусов:



Теорема синусов: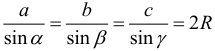



Радиус окружности, вписанной в правильный треугольник: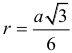



Радиус окружности, описанной около правильного треугольника: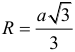



Площадь правильного треугольника: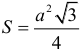



Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):



Радиус окружности, вписанной в прямоугольный треугольник:



Радиус окружности, описанной вокруг прямоугольного треугольника:



Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):



Свойства высоты, опущенной на гипотенузу прямоугольного треугольника: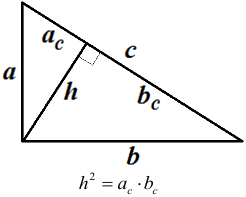







Длина средней линии трапеции:



Площадь трапеции: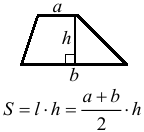



Площадь параллелограмма через сторону и высоту опущенную на неё:



Площадь параллелограмма через две стороны и угол между ними:



Площадь квадрата через длину его стороны:



Площадь квадрата через длину его диагонали:



Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):



Площадь прямоугольника через две смежные стороны:



Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:



Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):



Свойство касательных: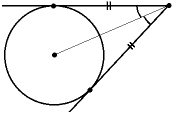



Свойство хорды: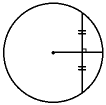



Теорема о пропорциональных отрезках хорд: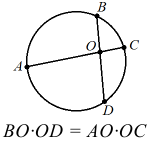



Теорема о касательной и секущей: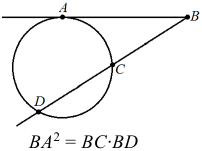



Теорема о двух секущих: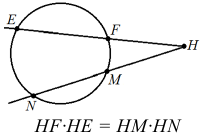



Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):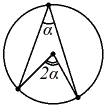



Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):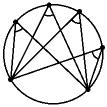



Свойство центральных углов и хорд: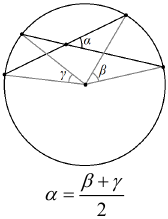



Свойство центральных углов и секущих: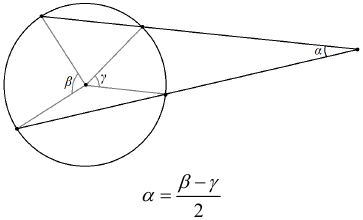



Условие, при выполнении которого возможно вписать окружность в четырёхугольник: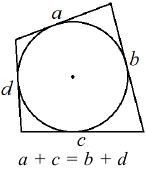



Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника: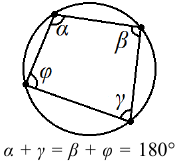



Сумма углов n-угольника:



Центральный угол правильного n-угольника:



Площадь правильного n-угольника:



Длина окружности:



Длина дуги окружности: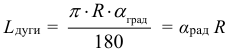



Площадь круга:



Площадь сектора: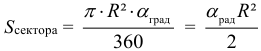



Площадь кольца:



Площадь кругового сегмента: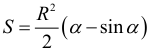



Геометрия в пространстве (стереометрия)

К оглавлению…

Главная диагональ куба:



Объем куба:



Объём прямоугольного параллелепипеда:



Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):



Объём призмы:



Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):



Объём кругового цилиндра:



Площадь боковой поверхности прямого кругового цилиндра:



Объём пирамиды:



Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):



Объем кругового конуса: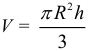



Площадь боковой поверхности прямого кругового конуса:



Длина образующей прямого кругового конуса:



Объём шара:



Площадь поверхности шара (или, другими словами, площадь сферы):



Координаты

К оглавлению…

Длина отрезка на координатной оси:



Длина отрезка на координатной плоскости:



Длина отрезка в трёхмерной системе координат:



Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):



Таблица умножения

К оглавлению…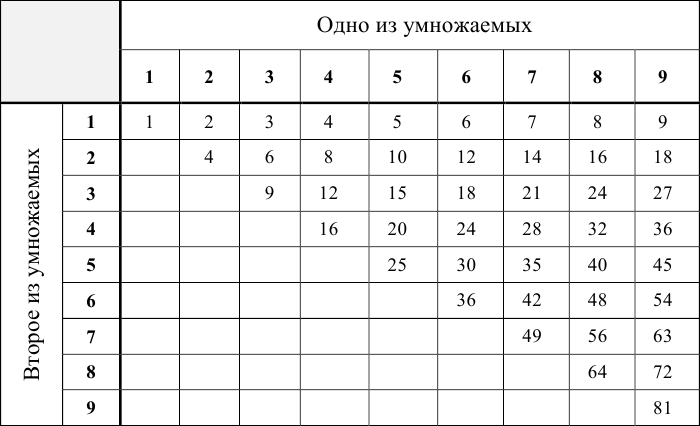



Таблица квадратов двухзначных чисел

К оглавлению…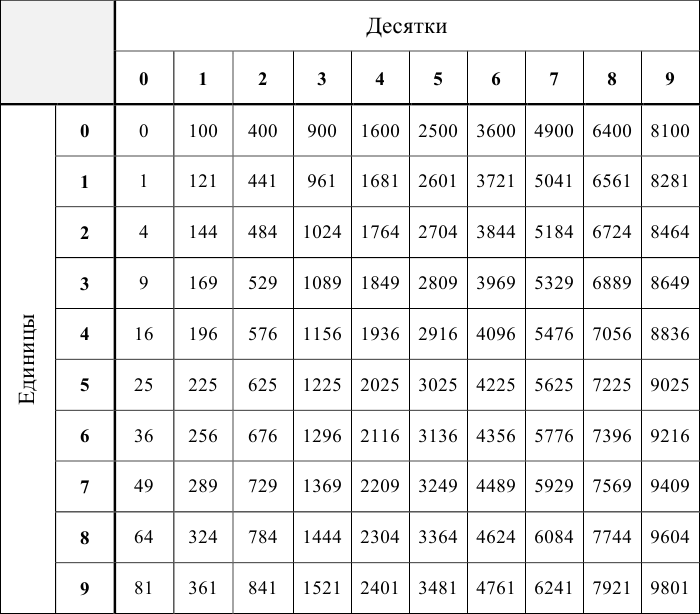



Расширенная PDF версия документа «Все главные формулы по школьной математике»: