вписанные и описанные многоугольники. ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ. Вписанная и описанная окружности

• Название: Вписанная и описанная окружности
• Анкор: вписанные и описанные многоугольники
• Дата: 07.05.2023
• Размер: 93.85 Kb.
• Имя файла: ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ.docx
• Тип: Решение; #1113301

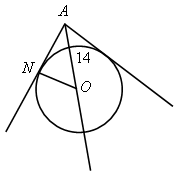
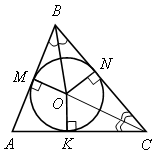
ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ

Цели: ввести понятие вписанной окружности и описанного около окружности многоугольника; рассмотреть теорему о том, что в любой треугольник можно вписать окружность.

Ход урока

I. Проверка домашнего задания.

Выполнить устно:

			1) а) Докажите, что АВМ = = МСА. б) АМ = 4, МD = 3, ВD = 4. Найдите расстояние от точки М до стороны АС.
		2) Найдите МKN и расстояние MN, если ОМ = , KМ = 3.
3) Найдите углы АВС, если ОАС = 20° и АОС = 120°.
	4) стороны угла А касаются окружности радиуса r с центром О. а) Найдите ОА, если r = 5 см, А = 60°.
	б) Найдите r, если ОА = 14 дм, А = 90°.

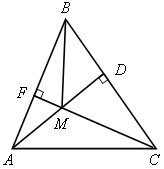
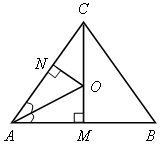
II. Изучение нового материала.

Изложить в виде лекции п. 74 до замечания 2.

III. Закрепление изученного материала.

Выполнить №№ 701 (для остроугольного треугольника), 689, 691.

№ 689.

Решение

1) Центр О вписанной окружности искомого радиуса r лежит на биссектрисе СМ треугольника АВС, а так как СМ АВ, то вписанная окружность касается отрезка АВ в точке М. Поэтому ОМ = r.

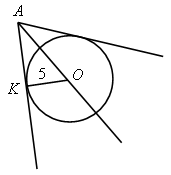
Далее обсудить с учащимися различные способы решения этой задачи:

I способ.

1. АМ = AB = 5 см.

2. M и N – точки касания, следовательно, AN = АМ = 5 см, откуда CN = АС – АN = 8 cм.

3. В АСМ : СМ = = 12 (см).

4. В СON : СО² = СN² + ON², то есть

(12 – r)² = 8² + r²

144 – 24r + r² = 64 + r².

r = 3 .

ОМ = ON = 3 см.

II способ.

1. В АСМ : АМ = AB = 5см.

СМ = = 12 (см).

2. Отрезок АО – биссектриса треугольника АМС (так как о – центр вписанной окружности), поэтому или ; 13r = 60 – 5r, r = 3 .

ОМ = ОN = 3 см.

IV. Итоги урока.

1) Центр вписанной в треугольник окружности в точке пересечения биссектрис; 2) ОМ = ON = ОK – радиусы вписанной окружности; 3) окружность единственная для данного треугольника.

Домашнее задание: вопросы 21, 22, с. 188; №№ 701

Стандартный вид числа

Цели: ввести понятие стандартного вида числа; формировать умение его применять при решении задач.

Ход урока

I. Организационный момент.

II. Устная работа.

– Заполните пустые клеточки:

а) 25 = ²; б) 81 = 3 ; в) 625 = (5²) ;

г) = 3 ; д) (а³)⁸ = а ; е) х^–8 = (х²) ;

ж) (у )¹⁴ = у^–28; з) (ab²)^–6 = a b ; и) .

III. Самостоятельная проверочная работа.

В а р и а н т 1

Упростить выражение:

1) 6х^–5у⁷ · 2,5х⁷у^–6; 3) ;

2) 3,2a⁶b : (0,8a³b^–3); 4) .

В а р и а н т 2

Упростить выражение:

1) ; 3) ;

2) ; 4) .

IV. Объяснение нового материала.

Согласно пункту учебника ввести понятие стандартного вида числа. Вынести на доску запись:

Стандартный вид числа: а · 10п, где 1 ≤ а < 10, п – целое число, п – порядок числа.

После этого дать учащимся задание, которое направлено на усвоение данного понятия.

З а д а н и е. Определить, какие из чисел записаны в стандартном виде, а какие – нет. Ответ объяснить:

а) 2,3 · 10⁹; г) 8 · 10^–5; ж) –3 · 10^–15;

б) 1,23 · 10^–11; д) 4,2 · 100⁵; з) 0,24 · 10^–17;

в) 15 · 10¹⁴; е) 5,8 · 10²³; и) 10 · 10⁴.

После усвоения понятия показать, как оно может быть применено на практике (разобрать примеры на с. 211–212 учебника).

V. Формирование умений и навыков.

1. № 1013 – устно.

2. Представьте в виде степени числа 10 выражение:

а) 1000 · 10^–6; д) 0,1 · 100 · 10^–5;

б) 10^–10 · 10^–5; е) 10000;

в) 10^–8 : 10⁴; ж) 0,001;

г) (10^–2)³; з) 0,01 · 100.

3. № 1014, № 1015 (б, г), № 1016 (б, г, е, з).

Р е ш е н и е

№ 1014.

а) 52000000 = 5,2 · 10⁷.

П р и м е ч а н и е. На этом примере разбираем, что в стандартном виде числа
а · 10^п, а [1; 10). В исходном числе мы перенесли запятую на 7 цифр влево, то есть уменьшили число в 10⁷ раз. Поэтому 52000000 больше 5,2 в 10⁷ раз.

б) 2180000 = 2,18 · 10⁶.

в) 675000000 = 6,75 · 10⁸.

г) 40,44 = 4,044 · 10¹.

д) 0,00281 = 2,81 · 10^-3.

П р и м е ч а н и е. На этом примере разбираем, что в исходном числе мы перенесли запятую на 3 цифры вправо, то есть увеличили число в 10³ раз. Поэтому 0,00281 меньше 2,81 в 10³ раз.

е) 0,0000035 = 3.5 · 10^–6.

№ 1015.

б) 117 · 10⁵ = 1,17 · 10² · 10⁵ = 1,07 · 10⁷;

г) 0,06 · 10⁵ = 6 · 10^–2 · 10⁵ = 6 · 10³.

№ 1016.

б) 6000000 = 6 · 10⁶;

г) 0,85 = 8,5 · 10^–1;

е) 0,000282=2,82 · 10^–4;

з) 0,042 · 10² = 4,2 · 10^–2 · 10² = 4,2 · 10⁰.

4. № 1017.

Р е ш е н и е

Масса Земли равна 6 · 10²¹ т.

Масса атома водорода равна 1,7 · 10^–21 г.

5. № 1018.

Р е ш е н и е

а) 3,8 · 10³ (т) = 3,8 · 10³ · 10³ (кг) = 3,8 · 10³ · 10⁶ (г) = 3,8 · 10⁹ (г);

б) 1,7 · 10^–4 (км) = 1,7 · 10^–4 · 10³ (м) = 1,7 · 10^–1 · 10² (см) = 1,7 · 10 (см);

в) 8,62 · 10^–1 (кг) = 8,62 · 10^–1 · 10^–3 (т) = 8,62 · 10^–4(т);

г) 5,24 · 10⁵ (см) = 5,24 · 10⁵ · 10^–2 (м) = 5,24 · 10³ (м).

6. Выполните действия. Результат запишите числом в стандартном виде:

а) (2,8 · 10⁵) · (2,5 · 10^–7);

б) (5,7 · 10⁴) : (3,8 · 10^–3);

в) 6,2 · 10^–2 + 4,8 · 10^–2.

Р е ш е н и е

а) (2,8 · 10⁵) · (2,5 · 10^–7) = (2,8 · 2,5) · (10⁵ · 10^–7) = 7 · 10^–2.

б) (5,7 · 10⁴) : (3,8 · 10^–3) = (5,7 : 3,8) · (10⁴ : 10^–3) = 1,5 · 10⁷.

в) 6,2 · 10^–2 + 4,8 · 10^–2 = 10^–2 · (6,2 + 4,8) = 11 · 10^–2 = 1,1 · 10^–3.

VI. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– Как записывается число в стандартном виде?

– Записаны ли числа 11 · 10⁸ и 0,93 · 10^–5 в стандартном виде? Почему?

– Если число записано в стандартном виде, что называется его порядком?

– Для чего на практике применяется запись чисел в стандартном виде?

Домашнее задание: № 1015 (а, в), № 1016 (а, в, д, ж), № 1019, № 1020, № 10226.
Транспортир, градус, алгоритм измерения углов
(п. 42, ч. 1)

Цель: научить давать определение градуса, обозначать его, измерять углы с помощью транспортира.

Ход урока

I. Оргмомент

II. Устные упражнения.

1. Кто быстрее сосчитает?



2. Назвать углы, изображенные на чертеже (задание проецируется на экран).



Найти среди этих углов прямые и развернутые углы.

III. Изучение нового материала.

На доске написан план.

1. Какой инструмент используют для измерения углов?

2. Как устроен транспортир?

3. Что такое градус? Каким знаком обозначают градус?

4. Как измеряют углы транспортиром?

Выделите три этапа: а) Совместить вершину развернутого угла на транспортире с углом, который мы измеряем; б) Один луч должен проходить через нулевую отметку (начало отсчета); в) второй луч проходит через отметку, которая показывает градусную меру угла.

IV. Закрепление.

1. № 1645, 1650, 1653 (устно), 1665, 1667.

V. Итог урока.

Повторить, как устроен транспортир, алгоритм измерения углов с помощью транспортира.

VI. Домашнее задание: п. 42 (ч. 1); № 1683, 1687, 1689. В математический словарь: транспортир, градус, алгоритм.
Решение задач

Цели: закрепить умение учащихся решать задачи с помощью систем уравнений; подготовить учащихся к контрольной работе.

Ход урока

I. Устная работа.

Придумайте задачу, для решения которой нужно составить систему уравнений:

II. Формирование умений и навыков.

1. № 1107.

Решение:

Пусть первый автомат изготовлял в час х деталей, а второй – у деталей. Заполним таблицу:

	А работа	k производительность	t время
первый автомат	3х дет.	х дет./ч	3 ч
второй автомат	2у дет.	у дет./ч	2 ч
совместная работа	2 (х + у) дет.	(х + у) дет./ч	2 ч

Составим и решим систему уравнений:



3х + 600 – 2х = 720;

х = 120;

2у = 600 – 2 · 120 = 360;

у = 180.

Ответ: 120 и 180 деталей.

2. № 1115.

Решение:

Пусть слиток золота весит х г, а слиток серебра весит у г. Согласно условию 9 слитков золота и 11 слитков серебра весят одинаково. Получим уравнение: 9х = 11у.

После того как поменяли местами один слиток золота с одним слитком серебра, на левой чаше оказалось 8 слитков золота и 1 слиток серебра, их общая масса равна (8х + у) г. На правой чаше стало 10 слитков серебра и 1 слиток золота, их общая масса равна (10у + х) г. По условию левая чаша на 13 г легче правой, значит, получим уравнение:

(10у + х) – (8х + у) = 13.

Составим и решим систему уравнений:



9y – y = 13;

81y – 77y = 117;

4у = 117;

у = 29,25;

х = ;

х = 35,75.

Ответ: 35,75 г и 29, 25 г.

3. № 1118.

Решение:

Пусть первая бригада по плану за месяц должна была изготовить х деталей, а вторая бригада – у деталей. По условию вместе они должны за месяц изготовить 680 деталей, то есть получим уравнение: х + у = 680.

Первая бригада, перевыполняя план, изготовила за месяц на 0,2х деталей больше, а вторая – на 0,15у деталей больше. По условию сверх плана было изготовлено 118 деталей, то есть получим уравнение:

0,2х + 0,15у = 118.

Составим и решим систему уравнений:



0,2 (680 – у) + 0,15у = 118;

136 – 0,2у + 0,15у = 118;

–0,05у = –18;

у = 360;

х = 680 – 360;

х = 320.

Ответ: 320 и 360 деталей.

Если останется время, можно предложить учащимся задачи повышенного уровня сложности.

4*. № 1120.

Решение:

Пусть на вклад «Депозитный» клиент положил х р., а на вклад «До востребования» – у р.

По условию всего клиент положил в банк 45000 р., то есть получим уравнение: х + у = 45000.

Доход от вклада «Депозитный» составил 9 %, то есть 0,09 х р., а от вклада «До востребования» 1 %, то есть 0,01у р. Общий доход клиента по условию равен 3410 р., значит, получим уравнение: 0,09х + 0,01у = 3410.

Составим и решим систему уравнений:





9х + 45000 – х = 341000;

8х = 296000;

х = 37000;

у = 45000 – 37000;

у = 8000.

Ответ: 37000 р. и 8000 р.

5*. № 1121.

Решение:

Пусть 10 %-ного раствора нужно взять х г, а 15 %-ного – у г.

Всего нужно получить 80 г раствора, то есть получим уравнение:
х + у = 80.

В х г 10 %-ного раствора содержится 0,1х г соляной кислоты, а в у г 15 %-ного раствора – 0,15у г соляной кислоты. В результате получили 80 г 12 %-ного раствора, в нём соляной кислоты 80 · 0,12 = 9,6 г.

Получим уравнение: 0,1х + 0,15у = 9,6.

Составим и решим систему уравнений:



80 – у + 1,5у = 96;

0,5у = 16;

у = 32;

х = 80 – 32 ;

х = 48.

Ответ: 48 г и 32 г.

III. Итоги урока.

– Что называется решением системы уравнений с двумя переменными?

– Какие существуют способы решения систем уравнений? Опишите каждый из них.

– Как решить задачу с помощью системы уравнений?

Домашнее задание: № 1114; № 1116; № 1117