ҚАРОР ҚАБУЛ ҚИЛИШ МАСАЛАЛАРИНИ КЛАССИФИКАЦИЯЛАШ ОПЕРАЦИЯЛАРНИ ТЕКШИРИШ. арор абул илиш масалаларини классификациялаш операцияларни текшириш масалаларининг типик синфлари
 Скачать 247.5 Kb. Скачать 247.5 Kb.
|
|
ҚАРОР ҚАБУЛ ҚИЛИШ МАСАЛАЛАРИНИ КЛАССИФИКАЦИЯЛАШ ОПЕРАЦИЯЛАРНИ ТЕКШИРИШ МАСАЛАЛАРИНИНГ ТИПИК СИНФЛАРИ Режа Қарор қабул қилиш масалаларини классификациялаш белгиси Самарадорлик мезони сони бўйича масалаларни синфларга ажратиш. Вақтга боғликлик бўйича масалаларни синфларга ажратиш. "Аниқлик - таҳлика - ноаниқлик" белгиси бўйича масалаларни синфларга ажратиш. Қарор қабул қилиш масалаларини ечиш усуллари. Операцияларни текшириш масалаларининг типик синфлари. Таянч иборалар Классификацион схема, классификациялаш белгиси, самарадорлик мезони, вақтга боғлиқлик, тасоддифийлик, ноаниқлик, статик, динамик, детерминисьтик, тахлика, математик программалаштириш, эхтимоллар назарияси, тажрибалар усули, уйинлар назарияси, минимакс назарияси, статистика, вариацион хисоб, оптимал бошкариш, конфликтли вазият, экспертлар фикри, синфларга бўлиш дарахти, захираларни бошкариш, ресурсларни таксимлаш, ускуналарни алмаштириш ва таъмирлаш, оммавий хизмат курситиш, тартиблаш, маршрут танлаш, комбинациялаш. 1. Қарор қабул қилиш масалаларини классификациялаш белгиси. Қарор қабул қилиш масалаларини турларга ажратиш учун хозирги замонда умум қабул қилинган классификацион схема мавжуд бўлмаганлиги туфайли бу масалаларни классификациялашда турли классификациялаш белгиларини асос қилиб олиш мумкин. Бундай белги сифатида масалан қуйидагиларни олиш мумкин: 1. Самарадорлик мезони сони, яъни операцияни утказувчи томон мақсадларига мос келувчи самарадорлик мезонининг ягона ёки кўп бўлиши. 2. Самарадорлик мезонининг ва чегаравий шартларининг вақтга боғлиқлиги ёки боғлиқ бўлмаслиги. 3. Операция параметрларини танлашда тассодифийлик ва ноаниқлик бўлиши ёки бўлмаслиги. 2. ҚАРОР ҚАБУЛ ҚИЛИШ МАСАЛАЛАРИНИ КЛАССИФИКАЦИЯЛАШ Биринчи классификацион белги буйича қарор қабул қилиш масалаларини икки турга ажратиш мумкин: бир критерияли (скаляр мақсад функцияли) ва кўп критерияли (вектор мақсад функцияли). Иккинчи классификацион белги буйича ҳам қарор қабул қилиш масалаларини икки синфга ажратиш мумкин: статик ва динамик. Статик масалаларда мақсад функцияси ва чегаравий шартлар вақт омилига боғлиқ бўлмайди. Динамик масалаларда эса бундай боғлиқлик бўлгани учун, улар статик масалаларга қараганда анча мураккаб бўлишади. Учинчи классификацион белгини "аниқлик - таҳлика - ноаниқлик" белгиси деб ҳам аталади. Бу белгига асосланиб қарор қабул қилиш масалаларини 3 турга ажратиш мумкин. 1. Аниқлик вазиятида қарор қабул қилиш ёки детерминистик қарор қабул қилиш. Бу масалаларда операция параметрлари қийматлари аввалдан операцияни текширувчига маълум бўлгани учун қарор қабул қилишда операцияни утказмасдан, бошқарилмайдиган омилларга боғлиқсиз равишда операцияни амалга ошириш имконияти мавжуд бўлади. 2. Таҳлика мавжуд ҳолларда қарор қабул қилиш ёки статистик қарор қабул қилиш. Бу масалаларда операция параметрлари қийматлари тасодифий характерга эга бўлгани учун операцияни утказувчи томонининг хар бир стратегияси мумкин бўлган натижалардан бирига олиб келиши мумкин. 3. Ноаниқлик вазиятида қарор қабул қилиш. Бу масалаларда самарадорлик мезони ва чегаравий шартлар операцияни текширувчи ихтиёрида бўлмаган, у аввалдан билмаган омиллар қатнашиши операция бўйича қарор қабул қилишни ута мураккаблаштиради. 3. Қарор қабул қилиш масалаларини ечиш усуллари. Энди қарор қабул қилиш масалаларини ечиш усулларига тухталиб утамиз. Бир самарадорлик мезони оптималлаштирилаётган статик детерминистик масалалар тадбиқий математиканинг тез ривожланаётган математик программалаштириш деб аталувчи бўлимида қаралаётган масалалардир. Шунинг учун, математик программалаштириш масалаларини ечиш усуллари тулалигича бу синф масалаларини ечиш учун қулланилиши мумкин. Бир критерийли статик масалалар таҳликали вазиятларда қаралса, бундай масалаларни эҳтимоллар назарияси ва математик программалаштириш усулларини қуллаб ечиш мумкин. Бундай масалалар синфи учун статистик тажрибалар усулини (бу усулнинг бошқа номи Монте-Карло усулидир) қуллаш мумкин. Бир критерийли статик масалалар аниқмаслик вазиятида қаралса, бундай масалалар учун қатор математик назариялар, жумладан, уйинлар назарияси, минимакс назарияси, статистика назарияси қўлланилади. Карор кабул килиш масалалари Бир критерийли масалалар Куп критерийли масалалар Статик масалалар Динамик масалалар             Аниклик вазиятида каралган масалалар Тахликали вазиятда каралган масалалар Ноаниклик вазиятида каралган масалалар Аниклик вазиятида каралган масалалар Тахликали вазиятда каралган масалалар Ноаниклик вазиятида каралган масалалар                    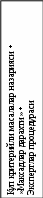          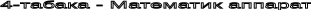 Динамик масалалар эса, хозирча, иқтисодий табиатли масалаларни ечиш учун кам қўлланилмоқда. Келажакда бу масалалар кенг куламда қўлланилиши кутилмоқда. Хозирги даврда эса бир критерийли динамик масалалар урганилмоқда. Бундай детерминистик масалалар сифатида классик математика бўлимларидан вариацион ҳисоб ва хозирги замон бўлимларидан оптимал бошқариш назарияси масалалари кўрилмоқда. Албатта, бундай масалалар ноаниқлик вазиятида яна ҳам чигаллашиб, мураккаблашиб, уларни ечиш анча мушкул бўлиб қолади. Конфликтли вазиятларда эса бундай масалалар уйинлар назариясининг бир бўлаги ҳисобланган дифференциал ўйинлар назарияси масалаларига боғланиб кетади. Динамик масалалар учун ҳам тахликали ва ноаниқлик вазиятларида экспертлар фикрларига асосланган процедуралар қўлланилади. Энг кам урганилган масалалар бу кўп критерийли иқтисодий масалалардир. Бунай масалалар мураккаб техник ва ташкилий-иқтисодий системаларга хос бўлиб, уларни урганиш учун «мақсадлар дарахти» деб аталган махсус ёндошиш қўлланилади. Ра-смда қарор қабул қилиш масалаларини синфларга бўлиш «дарахти» келтирилган. 4. ОПЕРАЦИЯЛАРНИ ТЕКШИРИШ МАСАЛАЛАРИНИНГ ТИПИК СИНФЛАРИ Операцияларни текшириш масалаларини системалаш уларни қўйидаги синфларга ажратишни тақоза қилади. заҳираларни бошқариш; ресурсларни тақсимлаш; ускуналарни таъмирлаш ва алмаштириш; оммавий хизмат кўрсатиш; тартиблаш; тармоқли режалаштириш ва бошқариш; маршрутни танлаш ва бошқалар. Саволлар Қарор қабул қилиш масалаларини классификациялаш белгиларини келтиринг. Самарадорлик мезони сони буйича масалаларни синфларга ажратинг. Вақтга боғлиқлик буйича масалаларни синфларга ажратинг. "Аниқлик - тахлика - ноаниқлик" белгиси буйича масалаларни синфларга ажратинг. Қарор қабул қилиш масалаларини ечиш усулларидан кайсиларини биласиз? Операцияларни текширишнинг типик масалалари канака? 5 - МАЪРУЗА ЧИЗИҚЛИ ПРОГРАММАЛАШТИРИШ МАСАЛАЛАРИ: КУЙИЛИШИ ВА УМУМИЙ ХАРАКТЕРИСТИКАСИ Режа Чизиқли программалаштириш масалаларининг кискача тарихи. Чизиқли моделларга мисоллар. Чизиқли программалаштириш масалаларининг математик модели. Чизиқли программалаштириш масалаларининг шартлари. Таянч иборалар Чизиқли программалаштириш, ишлаб чикариш масаласи, хом ашё, махсулот, сарфлаш нормаси, даромад, самарадорлик мезони, чеклашлар, узгарувчилар, мақсад функцияси, асосий шартлар,тугри шартлар, матрица, вектор, транспонирлаш, мумкин бўлган ечим, планлар туплами, оптимал план, каноник, нормал, тенгсизлик, тенглик. 1. Чизиқли программалаштириш иборасининг пайдо бўлиши Чизиқли программалаштириш математик программалаштиришнинг бир бўлими бўлиб, бунда номаълумларига чизиқли чеклашлар куйилган чизиқли функциянинг экстремал (максимал ёки минимал) қийматини топиш масаласини ечиш усуллари каралади.Чизиқли чеклашлар тенглик ёки каътий бўлмаган тенгсизлик куринишларида бўлишлари мумкин. Чизиқли программалаштириш масалалалрини системалашитириш ва уларни ечиш учун умумий, универсал усул яратиш устида Л.В.Конторович 1939 йилдан бошлаб шугиллана бошлаган. Америкалик олим Ж.Данциг томонидан 40-йилларда симплекс-усул деб аталувчи усул яратилди ва чизиқли программалаштириш назарияси ва унинг кулланиши тез суратлар билан ривожланди. "Чизиқли программалаштириш" иборасини биринчи бўлиб 1951 йилда Ж.Данциг ва Т.Кўпманс киритишган. Чизиқли программалаштиришнинг умумий масаласи куйидагича: Манфиймаслик шарти баъзи масалалар учун кисман ёки бутунлай бажарилмаслиги мумкин. 2. ЧИЗИҚЛИ МОДЕЛЛАРГА МИСОЛЛАР. 1.Ишлаб чикариш масаласи. Фараз қилайлик, корхонада m хил хом ашёдан n хил махсулот ишлаб чикарилсин. Хар бир i-хом ашёнинг умумий микдори (захираси) Масаланинг математик моделини тузиш учун ишлаб чикарилиши режалаштирилаётган j- махсулот микдорини Шундай қилиб, 2.Озука коришмаси хакидаги масала. Паррандачилик фермаси 20000 та жужани 8 хафта бокиб сотмокчи. Хар бир жужа 1 хафтада уртача 1 кг озука истеъмол қилади. Озука таркибида баъзи моддалар микдори чекланган: кальций микдори 0,8% дан кам эмас ва 1,2% дан кўп эмас, оксил 22% дан кам эмас, ширинлик 5% дан кўп эмас. Озука коришмаси тайёрлашда 3 хил озука махсулотидан фойдаланилади деб хисобланади. Бу махсулотлар нархи ва улардаги моддалар микдори куйидаги жадвалда келтирилган:
Минимал нархга эга бўлган озука коришмаси тузиш учун хар бир махсулотдан канча сотиб олиш керак? Бу масаланинг математик моделини тузиш учун куйидаги белгилашлар киритамиз: Коришманинг умумий вазни Математик модель куйидагича бўлади: 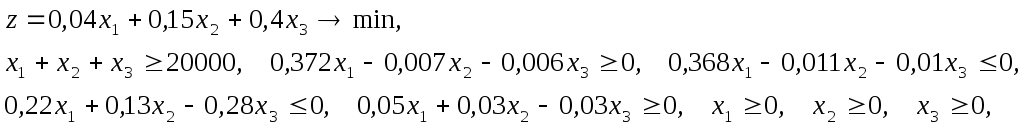 3. ЧИЗИҚЛИ ПРОГРАММАЛАШТИРИШ МАСАЛАЛАРИНИНГ МАТЕМАТИК МОДЕЛИ Маълумки корхонанинг ишини режалаштириш масаласининг математик модели куйидаги куринишда бўлади: Бу масалада Чизиқли програмалаштириш масаласи математик моделини вектор - матрица куринишда ҳам ёзиш мумкин: бунда 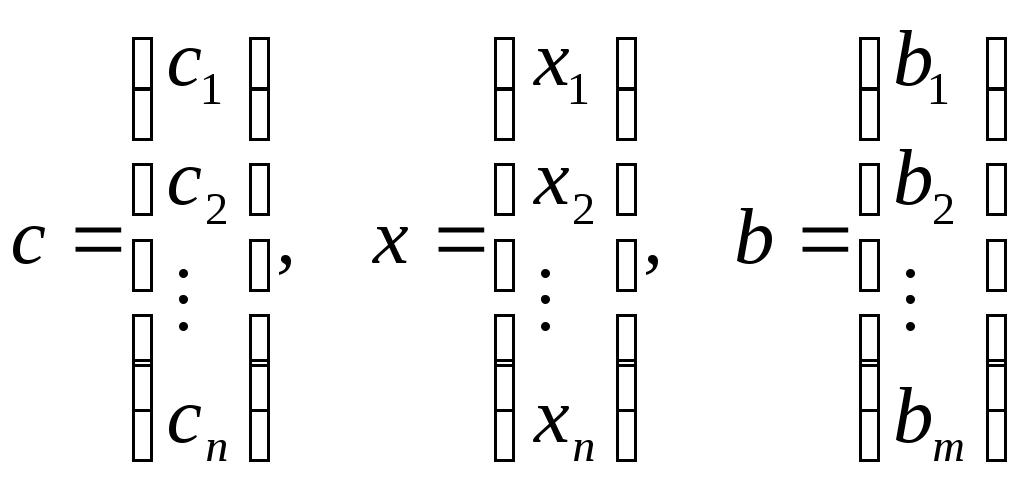 - векторлар, - векторлар, 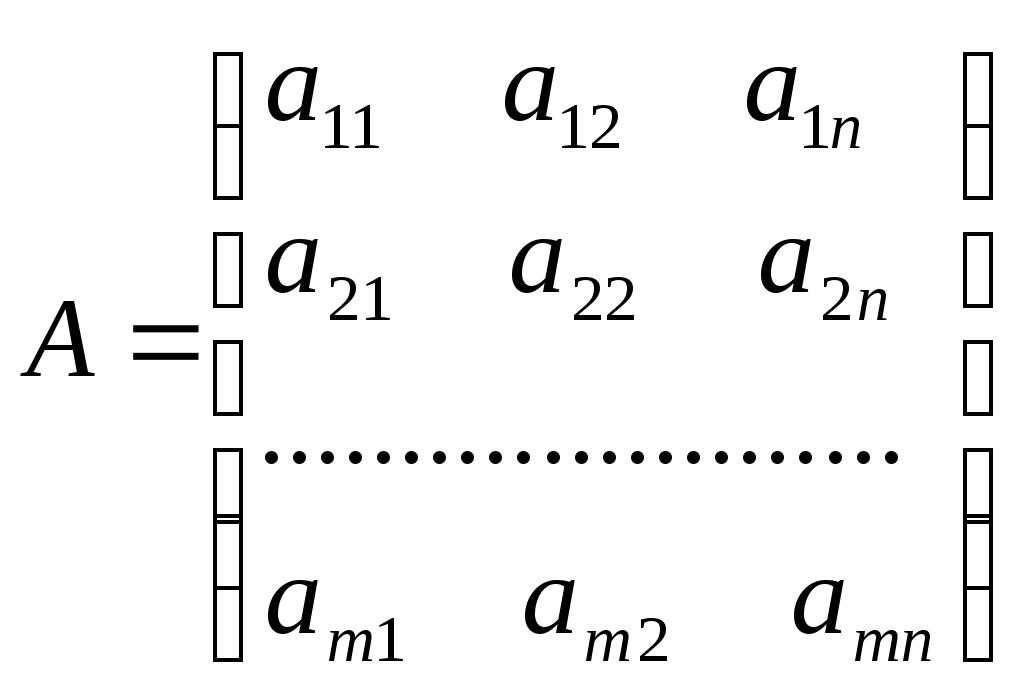 - матрица, - матрица,‘ – транспонирлаш. Чизиқли программалаштириш масаласининг барча (асосий ва тугри) шартларини каноатлантирувчи Агар Мисол. Куйидаги чизиқли програмалаштириш масаласи берилган бўлсин: 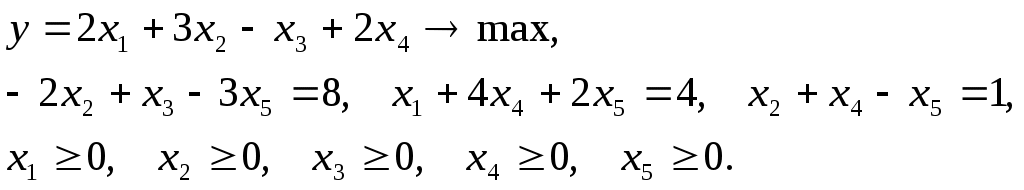 Бу масала учун бўла олмайди. Чизиқли программалаштириш масаласи Бундан ташкари, чизиқли программалаштириш масалаларининг бошка шаклллари ҳам мавжуд. Исботлаш мумкинки, ихтиёрий куринишда ёзилган чизиқли программалаштириш масаласини содда математик алмаштиришлар ёрдамида унга эквивалент бўлган бошка ихтиёрий куринишдаги чизиқли программалаштириш масаласига келтириш мумкин. Бунинг учун куйидаги алмаштиришлар кулланилади. 1) 2) тенгсизликни тенгламага айлантириш: 3) агар бирор узгарувчига тугри шарт куйилмаган бўлса, уни иккита манфиймас узгарувчилар айирмаси шаклида ифодалаш мумкин; 4) max ни min га ёки тескарига алмаштириш учун мақсад функциясининг ишораси тескарига алмаштирилади. Саволлар Чизиқли программалаштириш ибораси качон ва кимлар томонидан киритилган? Ишлаб чикариш масаласининг математик моделини ёзинг. Озука коришмаси масаласининг шартлари кандай? Чизиқли программалаштириш масаласининг вектор-матрица шакли кандай? План деб нимага айтилади? Оптимал план нима? Чизиқли программалаштириш масаласининг каноник куриниши кандай? Чизиқли программалаштириш масаласининг нормал куриниши кандай? 6 - МАЪРУЗА ЧИЗИҚЛИ ПРОГРАММАЛАШТИРИШ МАСАЛАЛАРИНИНГ ГЕОМЕТРИК МАЪНОСИ Режа Масаланинг куйилиши ва уни геометрик усулда ечиш шартлари. Мумкин бўлган ечимлар тупламини аниқлаш. Мақсад чизиклари. Таянч иборалар Узгарувчилар, текислик, декарт координаталар системаси, асосий шартлар, тугри чизик, ярим текислик, нукта, тугри шартлар, кўпбурчак, планлар туплами, буш, бушмас, чегараланган, чегараланмаган, кўпёкли, тугри чизиклар дастаси, нормал, нукта координаталари, чизиқли фазо, кесма, каварик, тупламлар кесишмаси, гипертекислик,тупламнинг четки нукталари, кўпёкли учлари. 1. МАСАЛАНИНГ КУЙИЛИШИ Содда холларда, яъни чизиқли программалаштириш масаласининг узгарувчилари сони 3 дан ошмаса уни геометрик тасвирлаш ва ечиш мумкин. Албатта, хаётда узгарувчилар сони 3 дан ошмаган чизиқли программалаштириш масалалари кам учрасада, улар чизиқли программалаштириш масалаларининг кўпчилик хоссалари ҳамда ечиш усулларини тушунишни анча осонлаштиради. Чизиқли программалаштириш масаласининг геометрик маъносини куйидаги жадвал учун ишлаб чикариш масаласини ечиш мисолида куриб чикамиз: m = 3, n = 2, 1- хом ашё ипак ип, 2- хом ашё - пахта ип, 3 - хом ашё – буёк.
Бу масаланинг геометрик маъносини англаш учун олдин унинг математик моделини тузамиз: бунда 2. ПЛАНЛАР СОХАСИНИ АНИҚЛАШ Тенгсизликда Маълумки, икки узгарувчили битта тенгсизлик текисликда тугри чизик ёрдамида ажратилган ярим тенгсизликлардан бирига мос келади (тугри чизик ҳам шу ярим текисликка тегишли). Ярим текисликларнинг кайси бири мос эканлигини аниқлаш учун чегарада (яъни тугри чизикда) ётмаган ихтиёрий нуктаниннг координаталарини тенгсизликка куйиб текшириш керак. Агар тенгсизлик каноатлантирилса, уша нукта жойлашган ярим текислик шу тенгсизликка мос, акс холда йук. О(0;0) нукта Тугри шартларга ҳам шу усулни куллаш мумкин. Натижада каралаётган масаланинг планлар тупламига мос туплам OABCD бешбурчак эканлигини топамиз (у шаклда штрихланган). Шуни таъкидлаш керакки, планир туплами буш, бушмас ва чегараланган (бизнинг мисомилиздагидек), бушмас ва чегараланмаган бўлиши мумкин. Агар планлар туплами бушмас ва чегараланган бўлса, у умуман олганда, кандайдир кўпёклига мос келади, кўпёкли чегараланган ёки чегараланмаган бўлиши мумкин (агар планлар туплами нукта, кесма, тугри чизик, полоса (яъни икки параллел тугри чизилар ораси) бўлса ҳам уни шартли равишда кўпёкли деб караймиз). Албатта n = 2 бўлган холда кўпёкли кўпбурчакка айланади. 3. МАҚСАД ЧИЗИКЛАРИ Энди мисолни карашда давом этиб, оптимал планни геометрик усул билан топишга уриниб курамиз. Шартга биноан мақсад функцияси, яъни 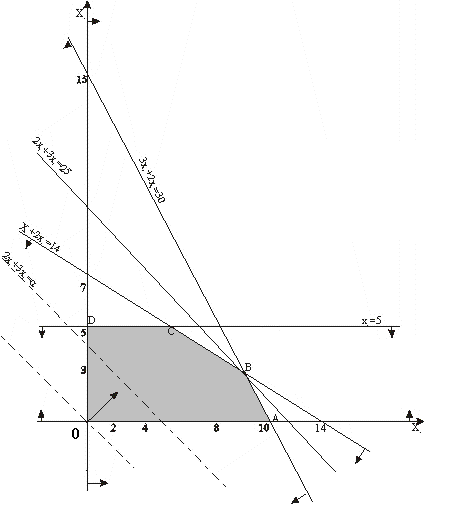 Шаклдан куриниб турибдики, Шундай қилиб, кохона 4. АСОСИЙ ТЕОРЕМАЛАР Аналитик геометрия курсидан маълумки, сон укида ётувчи хар кандай нукта битта хакикий сон оркали аниқланади. Шунинг учун, тугри чизикни бир улчовли чизиқли фазо деб аташ мусмкин. Текисликда жойлашган хар андай нукта иккита хакикий соннинг тартиблашган жуфти оркали аниқланади. Шунинг учун текислик 2 улчовли чизиқли фазо деб аталади. Уч улчовли чизиқли фазодаги хар кандай нукта учта хакикий соннинг тартибланган учлиги билан аниқланади. Кўпчилик масалаларда, шу жумладан, иктисодий масалаларда объектларни характерловчи факторлар n(n>3) та хакикий сон оркали ифодаланиши мумкин. Хар кандай n та хакикий соннинг тартибланган n лигини уз ичига олган тупламда кушиш ва скалярга кўпайтириш операциялари бажарилса бундай туплам n улчовли чизиқли фазо дейилади. n улчовли чизиқли фазони Агар Исботлаш мумкинки, исталган сондаги каварик тупламлар кесишмаси (буш бўлмаса) каварикдир. Теорема. Чизиқли программалаштириш масаласининг планлари туплами (буш бўлмаса) каварикдир. Исботи. Чизиқли программалаштириш масаласида факат икки хил шартлар мавжуд: чизиқли тенгсизлик ва чизиқли тенглама. Маълумки, чизиқли тенглама фазода гипертекисликни, тенгсизлик эса ярим фазони ифодалайди. Хар кандай гипертекислик ва хар кандай ярим фазо каварик тупламлар бўлгани учун чизиқли программалаштириш масаласининг планлари туплами (буш бўлмаса) каварик тупламлар кесишмаси сифатида каварикдир. Теорема исботланди. Чекли сондаги гипертекисликлар ва ярим фазолар кесишмаси буш бўлмаса уни каварик кўпёкли деб аталади. Шундай қилиб, чизиқли программмалаштириш масаласининг планлари туплами (буш бўлмаса) каварик кўпёклидир. Чизиқли программалаштириш масаласи мақсад функциясининг чизиқли эканлиги ва ва унинг планлари тупламининг каварик эканлиги асосида куйидаги теорема уринлидир. Теорема. Агар чизиқли программалаштириш масаласининг мақсад функцияси максимумга (минимумга) эриштирилаётган ва планлар тупламида юкоридан (куйидан) чегараланган бўлса, бундай масала оптимал ечимга эга. Биз геометрик усул билан чизиқли программалаштириш масаласини хал қилганда топилган оптимал ечим OABCD бешбурчакнинг В учида жойлашганлигини аниқлаган эдик. Исботлаш мумкинки, чизиқли программалаштириш масаласининг оптимал ечими унинг планлари тупламининг четки нукталари тупламида бўлади. Чизиқли программалаштириш масаласини ечиш усуллари планлар тупламининг четки нукталар орасида оптимал нуктани кидиришга асосланган. Бу усуллардан бири симплекс усулдир. Кўпёкликнинг учлари ҳам унинг четки нукталари тупламига тегишли бўлгани учун чизиқли программалаштириш масалсининг оптимал плани кўпёкликнинг бирорта учида жойлашган бўлади. Симплекс усулга кура планлар тупламини, яъни кўпёкликнинг четки нукталарини (аниқроги учларини) бирин-кетин текшира бориб, улар орасидан оптимал нуктани топиш мумкин. Саволлар Чизиқли программалаштириш масалаларидан кандайларини ечишга геометрик усулни куллаш мумкин? Асосий ва тугри шартлар кандай геометрик фигураларга мос келади? Планлар туплами кандай хоссаларга эга? Каварик туплам нима? Оптимал ечим планлар тупламининг каерида жойлашган бўлади? | ||||||||||||||||||||||||||||||||||||||||||||||||||
