Ким. КИМы для промежуточной аттестации 5-8 кл. 2021-2022. Аттестационная работа по математике для 5х классов
 Скачать 73.01 Kb. Скачать 73.01 Kb.
|
|
Аттестационная работа по математике для 5-х классов Вариант 1 № 1. Найдите значение выражения: (3,17 + 0,77 : 1,4) ∙ 3,5 – 4,216 = ? № 2. Поезд прошёл 168,3 км за 3,4 ч. Сколько километров он пройдёт за 5,8 ч с той же скоростью? № 3. Решите уравнение: 9,2х – 6,8х+ 0,64 = 1 № 4. На координатном луче отметить следующие дроби: 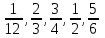 . .№ 5. Выполните действия: 15 : ( 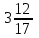 + +  ) + ( ) + (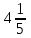 – – 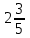 ) : 4. ) : 4.№ 6. Длина прямоугольного параллелепипеда равна 80 см. Его ширина составляет  его длины, а высота составляет его длины, а высота составляет  ширины. Вычислите объем ширины. Вычислите объем параллелепипеда. Вариант 2 № 1. Найдите значение выражения: (2,18 + 0,42 : 0,35) ∙ 1,5 – 3,827 = ? № 2. Автомобиль проехал 152,6 км за 2,8 ч. Сколько километров он проедет за 4,2 ч с той же скоростью? № 3. Решите уравнение: 9,4х – 7,8х+ 0,52 = 1. № 4. На координатном луче отметить следующие дроби: 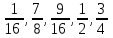 . .№ 5. Выполните действия: 20 : ( 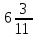 + + 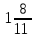 ) + ( ) + (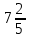 – –  ) : 5. ) : 5.№ 6. Длина прямоугольного параллелепипеда равна 60 см. Его высота составляет  его длины, а ширина составляет  высоты. Вычислите объем параллелепипеда. высоты. Вычислите объем параллелепипеда.Аттестационная работа по математике для 6-х классов Вариант 1 № 1. Вычислить: 1) ( –9,7 + 7,1) : 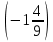 ; 2) ; 2)  . .№ 2. Решите уравнение: 1,2 (5х – 2) = 8 – ( 10,4 – 6х) . № 3. Баскетболом занимается 48 человек, а волейболисты составляют 7/8 количества баскетболистов и 70% от количества футболистов. Сколько человек занимается футболом? № 4. Расстояние между селами на карте равно 3,6 см. Найдите расстояние между селами на местности, если масштаб карты 1 : 200 000. № 5. Найдите неизвестный член пропорции: 2 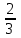 : 3 : 3 = х : 3,5 . = х : 3,5 .№ 6. На второй полке стояло в 4 раза больше книг, чем на первой. Когда на первую полку поставили еще 35 книг, а со второй убрали 25 книг, то на обоих полках книг стало поровну. Сколько книг было на каждой полке первоначально? № 7. Отметьте на координатной плоскости точки А(– 4; 2), В(0; – 3), С(5; 2). Проведите прямую АВ. Через точку С проведите прямую а, параллельную прямой АВ, и прямую в, перпендикулярную прямой АВ. Вариант 2 № 1. Вычислить: 1) ( –1,56 – 1,24)  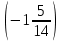 ; 2) ; 2) 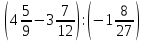 . .№ 2. Решите уравнение: 0,5 (8х + 1) = 1,5 – ( 2 – 4х) . № 3. В парке растёт 40 берёз, а каштаны составляют 45% от количества берёз и 6/11 количества дубов. Сколько дубов растёт в парке? № 4. Расстояние между селами на карте равно 4,3 см. Найдите расстояние между селами на местности, если масштаб карты 1 : 500 000. № 5. Найдите неизвестный член пропорции: х : 1,14 = 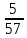 : :  . .№ 6. В первом ящике было в 5 раз больше яблок, чем во втором. Когда из первого ящика взяли 25 кг яблок, а во второй положили ещё 15 кг, то в обоих ящиках яблок стало поровну. Сколько килограммов яблок было в каждом ящике первоначально? № 7. Отметьте на координатной плоскости точки А(0; 4), В(– 3; – 2), Р(3; 6). Проведите прямую АВ. Через точку Р проведите прямую а, параллельную прямой АВ, и прямую в, перпендикулярную прямой АВ. Аттестационная работа по математике для 7-х классов Вариант 1 № 1. Упростить выражение: 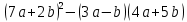 . .№ 2. Разложить на множители: 1)  ; 2) ; 2) 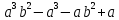 . .№ 3. Решить уравнение: 1) 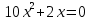 ; 2) ; 2) 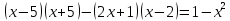 . .№ 4. Найдите четыре последовательных натуральных числа таких, что произведение третьего и четвёртого из этих чисел на 34 больше произведения первого и второго. № 5. Построить в одной системе координат графики функций у = х – 1 и у = – 2х + 8 и найти координаты точки их пересечения и координаты пересечения графиков функций с осями координат. № 6. Один из внутренних односторонних углов, образованных при пересечении двух параллельных прямых секущей на 700 больше другого. Найти эти углы. № 7. Найти углы равнобедренного треугольника, если один из его углов равен 1040. № 8. Периметр ∆АВС равен 72 см. Одна из сторон треугольника меньше второй на 12 см и меньше третьей в 2 раза. Вариант 2 № 1. Упростить выражение: 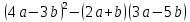 . .№ 2. Разложить на множители: 1) 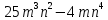 ; 2) ; 2)  . .№ 3. Решить уравнение: 1)  ; 2) ; 2) 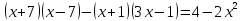 . .№ 4. Найдите четыре последовательных натуральных числа таких, что произведение второго и четвёртого из этих чисел на 31 больше произведения первого и третьего. № 5. Построить в одной системе координат графики функций у = 2х + 6 и у = – х + 3 и найти координаты точки их пересечения и координаты пересечения графиков функций с осями координат. № 6. Один из внутренних односторонних углов, образованных при пересечении двух параллельных прямых секущей на 600 меньше другого. Найти эти углы. № 7. Найти углы равнобедренного треугольника, если один из его углов равен 1020. № 8. Периметр ∆АВС равен 58 см. Одна из сторон треугольника больше второй на 12 см и больше третьей в 2 раза. Аттестационная работа по математике для 8-х классов Вариант 1 № 1. Найдите допустимые значения выражения и определите, при каких значениях переменной данное выражение равно нулю: 1) 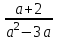 ; 2) ; 2)  . № 2. Найдите целые решения системы неравенств: . № 2. Найдите целые решения системы неравенств:  № 3. Решите систему уравнений: 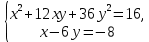 № 4. Расстояние между двумя сёлами, равное 6 км, велосипедист проезжает на 1 ч быстрее, чем проходит это расстояние пешеход. Найдите скорость каждого из них, если за 2 ч пешеход проходит на 4 км меньше, чем велосипедист проезжает за 1 ч. № 5. Постройте график функции f(x) = x2 – 4x + 3. Используя график, найдите: 1) область значений функции; 2) промежуток убывания функции; 3) множество решений неравенства f(x) > 0. № 6. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.  № 7. Найдите 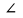 DEF , если градусные меры дуг DE и EF равны 150° и 68° соответственно. DEF , если градусные меры дуг DE и EF равны 150° и 68° соответственно.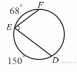 Вариант 2 № 1. Найдите допустимые значения выражения и определите, при каких значениях переменной данное выражение равно нулю: 1) 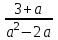 ; 2) ; 2)  . .№ 2. Найдите целые решения системы неравенств: 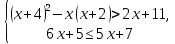 № 3. Решите систему уравнений:  № 4. Расстояние между двумя посёлками, равное 12 км, первый пешеход проходит на 1 ч быстрее № 4. Расстояние между двумя посёлками, равное 12 км, первый пешеход проходит на 1 ч быстрее второго. Найдите скорость каждого пешехода, если второй пешеход за 2 ч проходит на 2 км больше, чем первый за 1 ч. № 5. Постройте график функции f (х) = х2 – 2х – 8. Используя график, найдите: 1) область значений функции; 2) промежуток возрастания функции; 3) множество решений неравенства f (x) < 0. № 6. Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно. 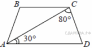 № 7. Найдите 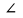 КОМ, если градусные меры дуг КО и ОМ равны 112° и 170° соответственно. КОМ, если градусные меры дуг КО и ОМ равны 112° и 170° соответственно.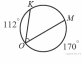 Аттестационная работа по математике для 9-х классов Вариант 1 Найти наименьшее целое решение неравенства: 11x – (3x + 4) < 9x – 7. Постройте график функции f (x) = –x2 – 6x – 5. Пользуясь графиком, найдите: 1) промежуток убывания функции; 2) множество решений неравенства –x2 – 6x – 5 < 0. Решите систему уравнений:  Найдите сумму первых семи членов арифметической прогрессии, если её третий член равен –5, а шестой равен 2,5. Две бригады, работая вместе, могут выполнить производственное задание за 6 ч. Если первая бригада проработает самостоятельно 2 ч, а потом вторая бригада проработает 3 ч, то будет выполнено 2/5 задания. За сколько часов каждая бригада может выполнить данное производственное задание самостоятельно? Две стороны параллелограмма равны 6 см и 8 см, а угол между ними равен 600. Найдите: 1) большую диагональ параллелограмма; 2) площадь параллелограмма. Докажите, что четырёхугольник АВСD с вершинами в точках А(1; – 1), В(– 4; 4), С(– 2; 6) и D(3; 1) является прямоугольником. Вариант 2 Найти наибольшее целое решение неравенства: 6x – 5(2x + 8) > 14 + 2x. Постройте график функции f (x) = x2 – 6x + 5. Пользуясь графиком, найдите: 1) промежуток возрастания функции; 2) множество решений неравенства x2 – 6x + 5 > 0. Решите систему уравнений: 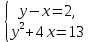 Найдите сумму первых одиннадцати членов арифметической прогрессии, если её четвёртый член равен 2,6, а шестой равен 1,2. Два тракториста, работая вместе, могут вспахать поле за 14 ч. Если первый тракторист проработает самостоятельно 7 ч, а потом второй тракторист проработает 14 ч, то будет вспахано 2/3 поля. За сколько часов каждый тракторист может вспахать это поле самостоятельно? Две стороны параллелограмма равны 3 см и 5 см, а угол между ними равен 300. Найдите: 1) большую диагональ параллелограмма; 2) площадь параллелограмма. Докажите, что четырёхугольник АВСD с вершинами в точках А(3; 5), В(– 1; – 1), С(– 7; –5) и D(–3; 1) является прямоугольником. |
