2 лаба. Автомобили и их характеристики
 Скачать 201.49 Kb.
|
|
Задача. Фирме необходимо перевезти 12-тонн груза на заданное расстояние. Фирма имеет в своем распоряжении автомобили «Газель», «Бычок» и «ЗИЛ-130». Характеристики автомобилей и их количество представлены в таблице 1. Сколько и каких автомобилей нужно задействовать, чтобы стоимость перевозки была минимальной? Таблица 1 – Автомобили и их характеристики
Математическая формулировка ЗЛО. Обозначим через n1, n2, n3 число автомобилей каждого типа, задействованных при перевозке. Ясно, что величины n1, n2, n3 должны быть целыми неотрицательными числами. Кроме этого указанные величины не должны превышать число автомобилей, имеющихся у фирмы. Таким образом, имеем 0≤ n1 ≤5; 0≤ n2 ≤3; 0≤ n3 ≤2. (1) Далее, суммарная грузоподъемность используемых автомобилей должна быть не менее 12 тонн. Это дает 1,5 n1 + 3 n2 + 5 n3 ≥ 12. (2) Наконец, требование минимальной стоимости перевозки приводит к следующему выражению для целевой функции f = 10n1 + 15n2 + 20n3 = min. (3) Численное решение задачи. 1. Запускаем MS Excel. 2. Выбираем на рабочем листе ячейки, куда будет помещено решение задачи (числа использованных автомобилей). Предлагается использовать для этой цели ячейки ВЗ, СЗ, D3. 3. Помещаем в ячейку В1 формулу для целевой функции, т.е. = 10*ВЗ + 15*СЗ + 20*D3. 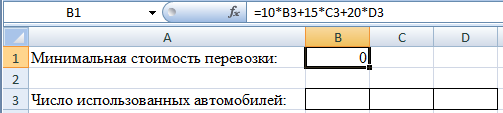 4. Помещаем в ячейку В4 формулу для суммарной грузоподъемности, т.е. = 1,5*B3 + 3*C3 + 5*D3. 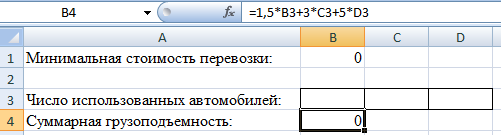 5. Вводим в ячейку А1 текст «Минимальная стоимость перевозки», в A3 – «Число использованных автомобилей», в А4 – «Суммарная грузоподъемность». 6. Выполняем команду «Данные/Поиск решения». 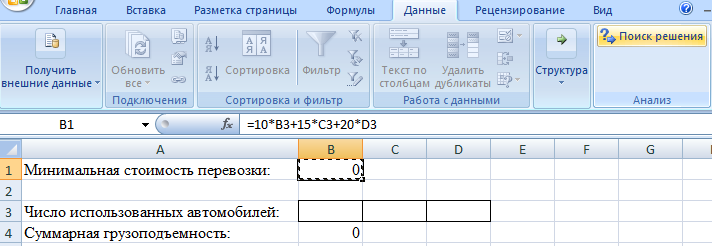 7. В открывшемся окне нажимаем на кнопку «Параметры». После открытия дополнительного окна устанавливаем флажок в поле «Линейная Модель». Закрываем дополнительное окно. 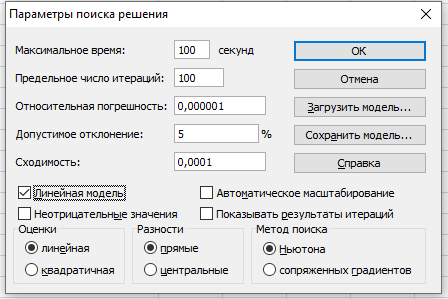 8. В окне «Поиск Решения» устанавливаем флажок в поле «Минимальное Значение». 9. Определяем адрес целевой ячейки (В1), т.е. ячейки с формулой для целевой функции. 10. Определяем изменяемые ячейки (B3:D3), куда будет помещено решение задачи. 11. Вводим ограничения на решение с помощью кнопки «Добавить». Они имеют следующий вид: В4 ≥ 12; B3:D3≥0; B3:D3 = целое; ВЗ ≤ 5; C3 ≤ 3; D3 ≤ 2. 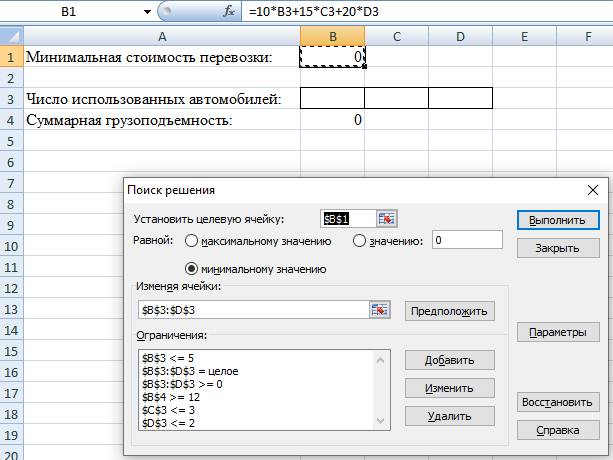 12. Нажимаем на кнопку «Выполнить». 13. В открывшемся окне подсвечиваем поле «Результаты». Нажимаем на кнопку ОК. 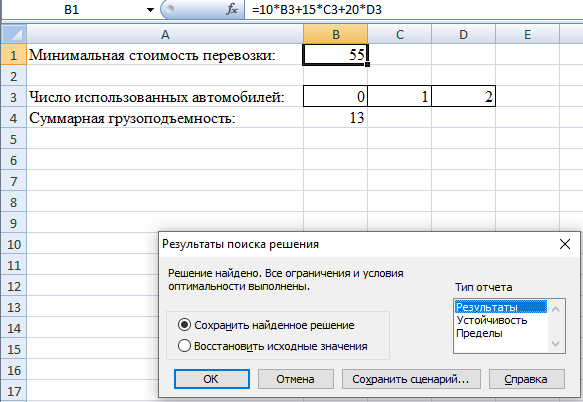 Открывается окно с отчетом о результатах решения. 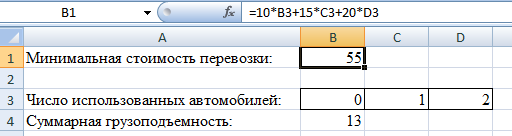 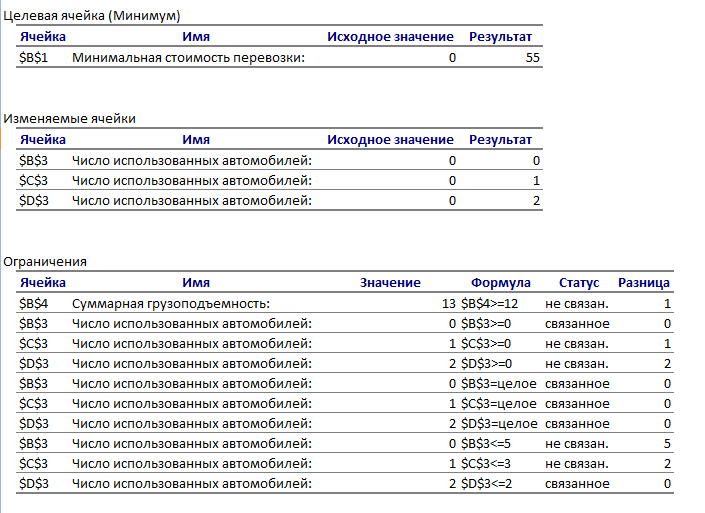 Отобразим графически полученные результаты. Так как автомобили «Газель» в решении не присутствуют, то построим график в плоскости Оn2n3. Целевая функция в проекции на эту плоскость: f = 15n2 + 20n3 = min, Пусть min = 20, построим прямую. Пусть n2 = 0, тогда n3 = 1; пусть n2 = 1, тогда n3 = 1/4. Чтобы найти минимум функции, нужно перемещать прямую параллельно построенной прямой. Область допустимых значений: 3 n2 + 5 n3 ≥ 12. Пусть n2 = 0, тогда n3 = 2,4; пусть n2 = 2, тогда n3 = 1,2. Ограничения по количеству автомобилей: 0≤ n2 ≤3; 0≤ n3 ≤2. О  бласть допустимых значений – треугольник АВС  n3    2 А В 1 С 0 1 2 3 n2 Минимум будет наблюдаться в точке с координатами n2 = 1, n3 = 2. |