реферат. 4 апта. азастан республикасыны ауыл шаруашылыы м инистрлігі
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
Мазмұны Кіріспе......................................................................................................................3 ІІ. Негізгі бөлім........................................................................................................4 1. Эйлердің дифференциалды теңдеулері.............................................................4 2. Нақты сұйықтық ағыны үшін Бернулли теңдеуі..............................................6 Қорытынды..............................................................................................................7 Пайданылған әдебиеттер Кіріспе Бір айнымалы функцияның туындысы бар теңдеу қолданбалы математиканың көптеген салаларында пайда болады. Жалпы алғанда, бір айнымалының басқа айнымалыға қатысты өзгеру дәрежесі қарастырылатын кез-келген физикалық жағдай дифференциалдық теңдеумен сипатталады және мұндай жағдайлар жиі кездеседі. Бастапқы деректермен қарапайым бірінші ретті дифференциалдық теңдеулерді (сызықты емес) шешу (Коши есебі) сандық әдістерді қолданудың классикалық саласы болып табылады. Көптеген айырмашылық әдістері бар, олардың кейбіреулері үй дәуірінде пайда болды және қазіргі заманғы компьютерлерге жарамды болды. Бастапқы деректермен қарапайым бірінші ретті дифференциалдық теңдеулерді (сызықты емес) шешу сандық әдістерді қолданудың классикалық саласы болып табылады. Көптеген айырмашылық әдістері бар, олардың кейбіреулері үй дәуірінде пайда болды және қазіргі заманғы компьютерлерге жарамды болды. Эйлер әдісі Бұл алғашқы ретті қарапайым дифференциалдық теңдеудің сандық шешімдерін табу үшін қолданылатын процедуралардың ішіндегі ең негізгісі және қарапайымы, егер оның бастапқы шарты белгілі болса. Қарапайым дифференциалдық теңдеу (ODE) - бұл бір тәуелсіз айнымалының белгісіз функциясын оның туындыларымен байланыстыратын теңдеу.  Сурет 1. Егер теңдеуде пайда болатын ең үлкен туынды бірінші дәрежелі болса, онда бұл бірінші дәрежелі қарапайым дифференциалдық теңдеу. Бірінші дәрежелі теңдеуді жазудың ең жалпы әдісі: x = x0 y = y0 Бернулли теңдеуі – гидромеханиканың негізгі теңдеулерінің бірі. Бұл теңдеуді швейцариялық ғалым Д. Бернулли (1700 — 1782) өзінің 1738 жылы Страсбургте жарық көрген “Гидродинамика” деген еңбегінде тұжырымдаған. Бернулли теоремасы, қозғалатын сұйықтықтың мінез-құлқын сипаттайтын, математик және физик Даниэль Бернулли өз жұмысында айтқан Гидродинамика. Тұжырымға сәйкес, тұйықталған өткізгіш арқылы айналатын идеалды сұйықтық (үйкеліссіз және тұтқырлықсыз) өз жолында тұрақты энергияға ие болады. Теореманы энергияны сақтау принципінен және тіпті Ньютонның екінші қозғалыс заңынан шығаруға болады. Сонымен қатар, Бернулли принципі сұйықтықтың жылдамдығының жоғарылауы оған әсер ететін қысымның төмендеуін, оның потенциалдық энергиясының төмендеуін немесе екеуін де бір мезгілде білдіреді дейді. Бернулли теоремасы ғылым, инженерия, спорт және т.б. сияқты әр түрлі салаларда көптеген және әр түрлі қолданыста болады. Камин дизайнында қызықты қосымша табылған. Түтіндер негіз мен түтіннің шығысы арасындағы қысымның үлкен айырмашылығына қол жеткізу үшін жоғары салынған, соның арқасында жану газдарын шығару оңайырақ. Әрине, Бернулли теңдеуі құбырлардағы сұйық ағындарының қозғалысын зерттеуге де қатысты. Теңдеуден құбырдың көлденең қимасының ауданын азайту, ол арқылы өтетін сұйықтықтың жылдамдығын арттыру үшін қысымның төмендеуін де білдіреді. 2.1 Эйлердің дифференциалды теңдеулері. У/ =F(x,y) дифференциалдық теңдеуін сандық әдіспен шешу дегеніміз - у=F(x) функциясын анықтамай , х0, х1..., хп және у0 сандарының берілген тізбегі үшін у =F(xi )(i=1,2,..., n) және F(x0 )=y0 мәндерін табыңыз . Осылайша, сандық әдістер функцияны табудың орнына мүмкіндік береді Y=F (x) берілген аргументтер тізбегі үшін осы функцияның мәндер кестесін алыңыз. H=xk-xk-1 шамасы интегралдау қадамы деп аталады. Эйлер әдісі қажетті y(x) функциясының жуық мәндерінің кестесі түрінде шешім беретін сандық әдістерге жатады. Бұл салыстырмалы түрде өрескел және негізінен индикативті есептеулер үшін қолданылады. Алайда, Эйлер әдісіне негізделген идеялар бірқатар басқа әдістер үшін бастапқы болып табылады. Бірінші ретті дифференциалдық теңдеуді қарастырыңыз: y/ =f(x,y) (1) бастапқы шартпен x=x0 , y(x0 )=y0 (2) [А,b] кесіндісінде (1) теңдеудің шешімін табу қажет. [A, b] кесіндісін N тең бөліктерге бөліп , x0 , x1, x2,..., XP тізбегін аламыз, мұндағы xi =x0 + ih(i=0,1,..., n), ал h=(b-a)/N-интеграция қадамы. Эйлер әдісінде у(хі )"yi" жуық мәндері уі +hf(xi , yi ) (i=0,1,2...) формулалары бойынша рет-ретімен есептеледі. Бұл жағдайда M0(x0, U0) нүктесі арқылы өтетін u=u (x) интегралдық қисығы M0 М1 М2 ... мі (xi , yi) шыңдарымен ауыстырылады (i=0,1,2,...); Mi Mi+1-дің әрбір буыны Эйлер сынған деп аталады , mi нүктесі арқылы өтетін теңдеудің (1) интегралдық қисығының бағытына сәйкес келетін бағытқа ие, 1-суретті қараңыз. 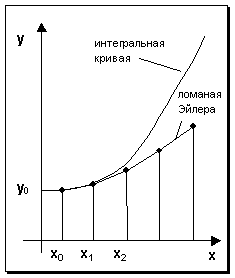 Сурет 2. Егер (1) теңдеудің оң жағы R{|x-x0 |£a, |y-y0 |£b}төртбұрыштағы болса, шарттарды қанағаттандырады: |f(x, y1 )- f(x, y2 )| £ N|y1 -y2 | (N=const), |df/dx|=|df/dx+f(df/dy)| £ M (M=const), онда қатені келесі бағалау бар: |y(xn )-yn | £ hM/2N[(1+hN)n -1], (3) мұндағы у(хп) - теңдеуді дәл шешудің мәні(1) х=хп кезінде , ал уп-N-қадамда алынған шамаланған мән. Формула (3) негізінен теориялық қолданысқа ие. Іс жүзінде кейде екі есе есептеу ыңғайлы болады : алдымен есептеу h қадамымен жасалады, содан кейін қадам ұсақталады және қайта есептеу қадаммен жүзеге асырыладыһ/2. Уп * неғұрлым дәл мәнінің қателігі формуламен бағаланады |yn -y(xn )|»|yn * -yn |. (4) Эйлер әдісі дифференциалдық теңдеулер жүйесіне және жоғары ретті дифференциалдық теңдеулерге оңай таралады. Соңғылары алдымен Бірінші ретті дифференциалдық теңдеулер жүйесіне келтірілуі керек. Түзетілген Эйлер әдісі Түзетілген Эйлер әдісінде біз екі нүкте үшін тангенс көлбеуінің орташа тангенсін табамыз: xm, ym және xm +h, ym +hy ' m . Соңғы нүкте қарапайым әдіспен XM+1, ym+1 деп белгіленген . XM+1, ym+1 нүктелерін табудың геометриялық процесін 2-суреттен байқауға болады. Эйлер әдісін қолдана отырып, L1 сызығында орналасқан XM +h, ym +hy ' M нүктелері орналасқан. Осы кезде тангенс бұрышының тангенсі қайтадан есептеледі, суретте L2 түзу сызық осы мәнге сәйкес келеді . Екі тангенстің орташа мәні L'3 түзу береді . Соңында , XM, ym нүктесі арқылы біз L'3-ке параллель L3 сызамыз . L3 Түзу нүктесі x= xm+1 =xm +h қалпына келтірілген ординатамен қиылысады және y= ym+1 = ym +hy ' m қалаған нүктесі болады . L3 көлбеу бұрышының тангенсі: F(xm , ym )=1/2[f(xm , ym )+f(xm +h, ym +hy’m )], (5) мұндағы ym = f(xm , ym ) (6) L3 сызығының теңдеуі келесі түрде жазылады: y = ym + (x - xm )*F(xm ) (7) сондықтан: ym+1 = ym + h*F(xm ) (8) 5, 6, 7 және 8 коэффициенттері түзетілген Эйлер әдісін сипаттайды. 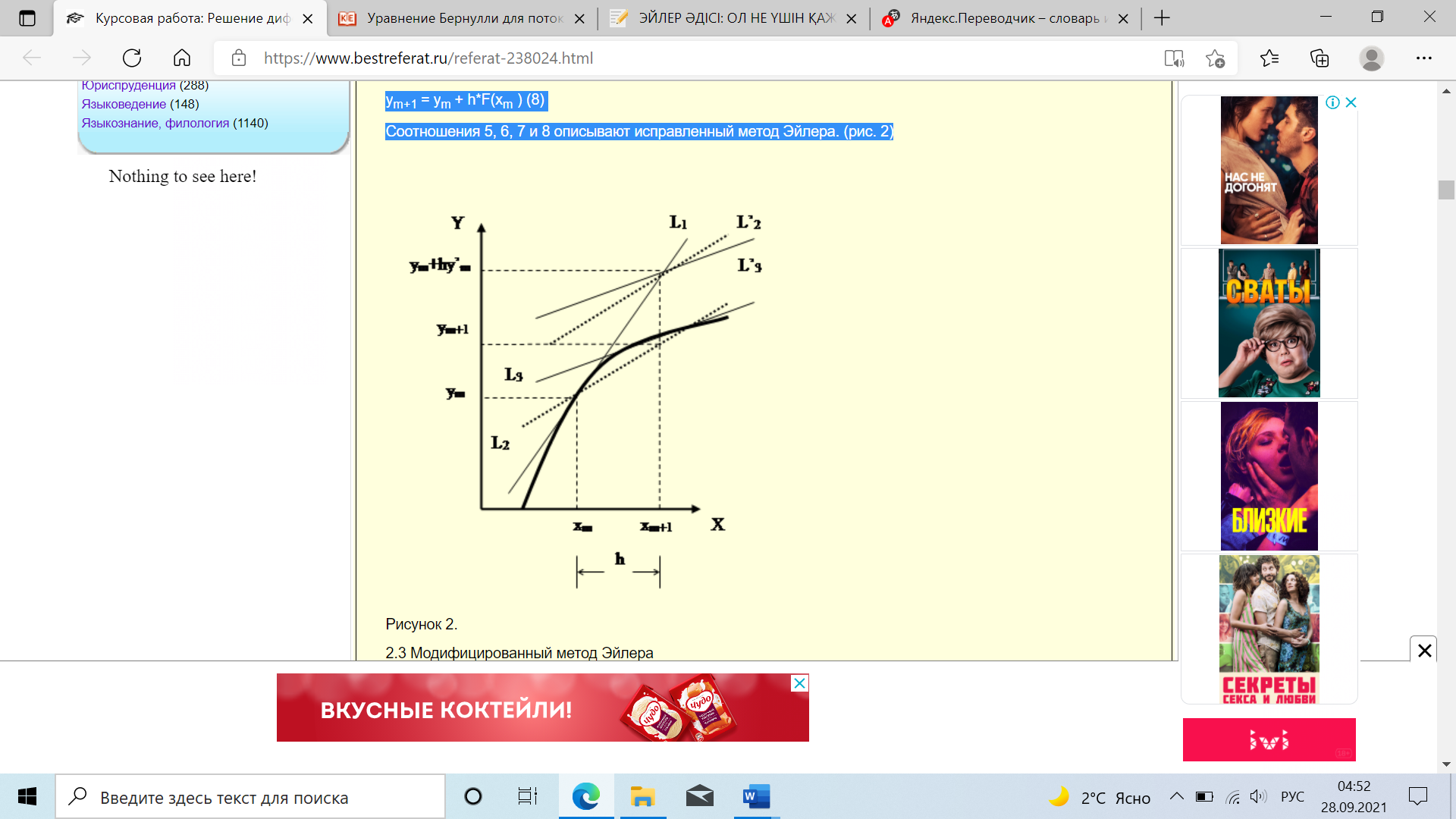 Сурет 3. 2.3 Нақты сұйықтық ағыны үшін Бернулли теңдеуі. z1 + (p1/pg) + (V12/2g = z2 + (p2/pg) + (V22/2g) мұндағы: z-геометриялық биіктік, таңдалған бөлімдегі p-қысым, V - таңдалған бөлімдегі сұйықтықтың жылдамдығы, ρ-сұйықтықтың тығыздығы, g-еркін құлаудың үдеуі. Бұл теңдеу идеалды сығылмайтын сұйықтықтың қарапайым ағымы үшін заң немесе Бернулли теңдеуі деп аталады. Қарастырылып отырған әрбір бөлім үшін толық қысым геометриялық, пьезометриялық және жылдамдық қысымының қосындысы болып табылады. Идеал сұйықтық үшін (яғни энергия шығыны болмаған кезде) толық қысым тұрақты болады. Бернулли теңдеуінің физикалық мағынасы Бернулли теңдеуінің құрамдас бөліктері сұйықтықтың меншікті (масса бірлігіне жататын) механикалық энергиясының әртүрлі формалары болып табылады: gz-позицияның нақты энергиясы, p / ρ - қозғалатын сұйықтық қысымының нақты энергиясы, V12 / 2-Сұйықтықтың кинетикалық энергиясы, gz + p/ρ + V2 / 2 = Hg - қозғалатын идеалды сұйықтықтың жалпы нақты энергиясы. Бернулли теңдеуінің физикалық және энергетикалық мәні идеалды сұйықтықтың элементар ағыны бойымен толық нақты энергияның тұрақтылығында жатыр. Нақты тұтқыр сұйықтық ағыны үшін Бернулли теңдеуі Егер есептелген бөлімдер арасындағы учаскеде механикалық жұмыс жасалмаса және қозғалыс сұйықтық ағынсыз және алынбай тұрақты болса және сұйықтықтың өзі сығылмайтын болса, онда ағынның тәуелділігі әділ болады: Н1=Н2 + Δh1-2 z1 + p1/pg + V12/2g = z2 + p2/pg + V22/2g + Δh1 - 2 Бернулли теңдеуі идеалды сығылмайтын сұйықтық үшін механикалық энергияның сақталу заңын көрсетеді. 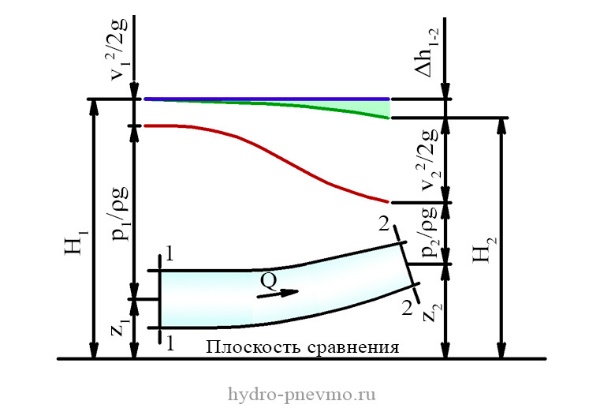 Сурет 4. Бернулли теңдеуі 1-1 және 2-2 шектеулі қималары бар аймақтағы сұйықтық ағынының толық қысымы арасындағы байланысты орнатады. Бернулли теңдеуіне сәйкес Hi ағынының толық қысымы 1-1 бөлімнен 2-2 қимаға дейін учаскенің гидравликалық кедергісінен туындаған H1 - 2 қысым (энергия) ысырабының мөлшеріне азаяды. Бернулли теңдеуі гидравликаның ең маңызды заңдарының бірінің өрнегі болып табылады. Себебі оның негізгі міндеттерінің шешуі энергия шығымын анықтаумен және жұмысты немесе қуаты есептеумен байланысты. Бернулли теңдеуін қолдана отырып сұйықтың жылдамдығы мен шығымын, яғни, аппараттар мен құбыр өткізгіштердің өткізу қабілеттілігін анықтайды. Сонымен қатар бұл теңдеудің көмегімен сұйықтың ағу уақытын және оның толық тегеурінің есептейді. Қорытынды Эйлер әдісі дифференциалдық теңдеулерді шешуге мүмкіндік беретін, қойылған есепті берілген дәлдік дәрежесімен сандық шешу мүмкіндігін көрсететін дайын бағдарламалық өнім болып табылады. Бұл бағдарлама пайдаланушы анықтаған дифференциалдық теңдеуді ең аз уақыт аралығында шешеді. Бұл жағдайда Пайдаланушыға алынған шешімнің кестесін ескере отырып, шешімді көзбен бағалау мүмкіндігі беріледі. Бағдарламаның артықшылықтары сонымен қатар ыңғайлы пайдаланушы интерфейсін, жеке дифференциалдық теңдеулерді енгізу мүмкіндігін, сондай-ақ ұзақ уақыт бойы жоғары тұрақтылықты қамтиды. Алайда кейбір кемшіліктер бар. Бағдарламаның кемшіліктері: пайдаланушы енгізген теңдеулердің маңыздылығы, ерекше оқиғаларды өңдеудің болмауы. Бұл, әрине, бағдарламаның мүмкіндіктерін шектейді. Бернулли Заңы тұрақты сұйықтық ағынының жылдамдығы мен оның қысымы арасындағы байланысты орнатады. Осы Заңға сәйкес, егер сұйықтықтың қысымы ток сызығы бойымен жоғарыласа, онда ток жылдамдығы төмендейді. Бернулли интегралы ретінде заңның сандық көрінісі идеалды сұйықтықтың гидродинамикалық теңдеулерін интеграциялаудың нәтижесі болып табылады (яғни тұтқырлық пен жылу өткізгіштік жоқ). |

 ИНИСТРЛІГІ
ИНИСТРЛІГІ