Лабораторная (вариант 2). Б) среднее квадратическое отклонение (ско) в) оценку ско

• Название: Б) среднее квадратическое отклонение (ско) в) оценку ско
• Дата: 18.10.2021
• Размер: 135 Kb.
• Имя файла: Лабораторная (вариант 2).doc
• Тип: Документы; #250061

Цель работы. Изучение видов, методов, средств и погрешностей измерений. Получение практических навыков планирования и обработки результатов прямых и косвенных измерений.
1. В результате равноточных измерений были получены 10 значений измеряемой величины (таблица 1), для обработки которых необходимо определить:

а) среднее;

б) среднее квадратическое отклонение (СКО);

в) оценку СКО;

г) определить наличие грубых ошибок в результатах измерений;

д) доверительный интервал с доверительной вероятностью .

Результат записать с учетом правила округления.
Таблица 1 – Результаты прямых измерений

№ вар	Измеряемая величина	1	2	3	4	5	6	7	8	9	10
2	R, Ом	68,5	67,8	65,8	60	70,1	63,8	68,4	65,3	66,1	65,9

Выполнение
Определим истинное значение измеряемой величины по формуле 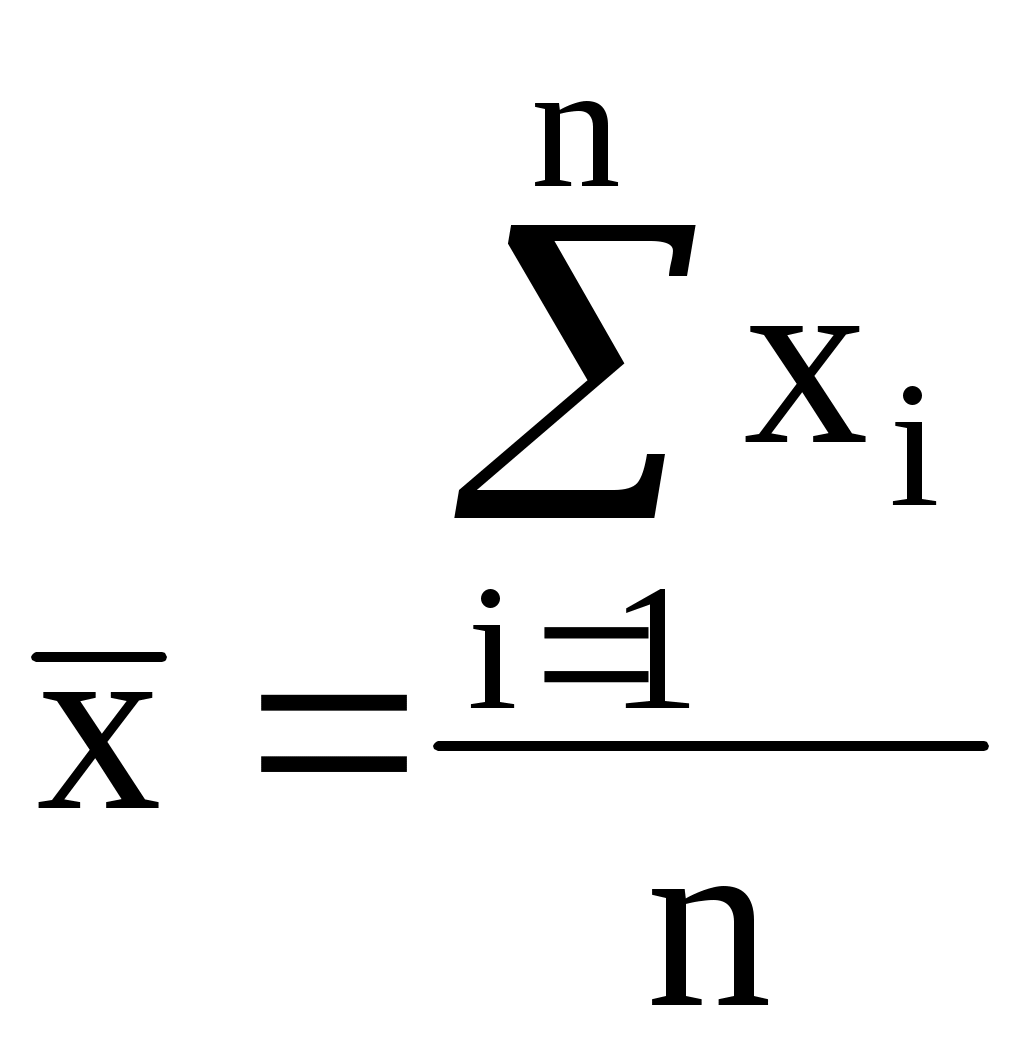(1):
, (1)
где n – количество измерений;

– результаты наблюдений.

Тогда:
Ом.
Определим среднеквадратическое отклонение по формуле (2):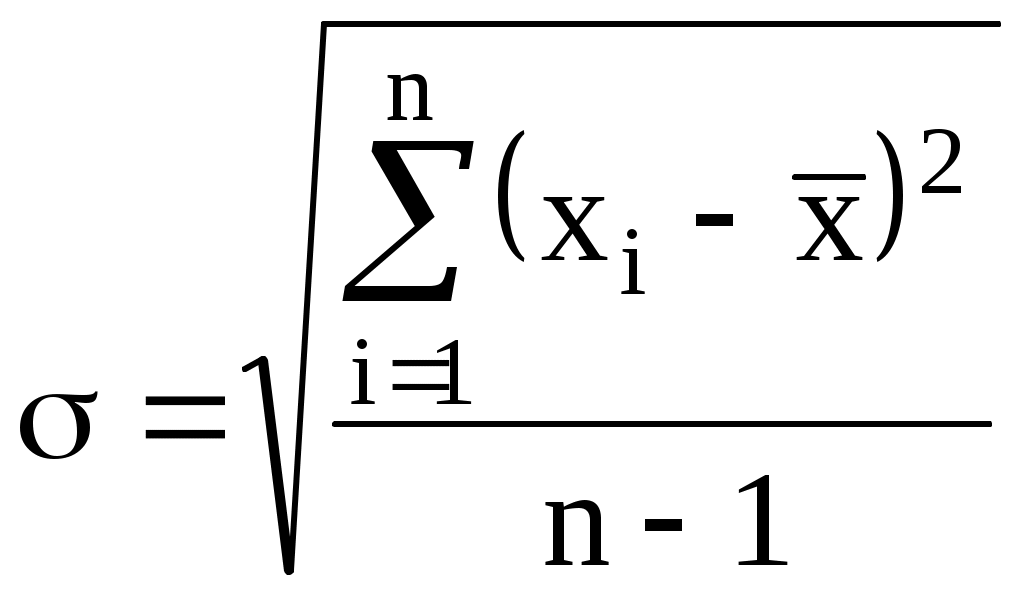
, (2)
Ом.
Определим наличие грубых ошибок в результатах наблюдения при помощи критерия Романовского. Сначала вычислим параметры и по формулам (3) и (4) соответственно:
, (3)
, (4)
,
.
Критическое значение критерия Романовского при доверительной вероятности =0,95 и количестве измерений n=10 равен =2,568.

Поскольку < и < , то грубых ошибок в результатах наблюдений нет.

Определим оценку среднего квадратического отклонения по формуле (5):
, (5)
Ом.
Доверительный интервал при :
Ом.
Результат измерения (с учётом правил округления):
Ом, =0,95.
2. Предполагая, что действительное значение измеряемой величины получено при измерении прибором заданного предела измерения и заданного класса точности (таблица 2), определить абсолютную погрешность данного результата измерения. Записать результат.
Таблица 2 – Исходные данные

№ вар	Предел измерения прибора	Класс точности прибора
2	100 Ом

Выполнение
Класс точности прибора . Такое обозначение применяют для приборов, у которых предел допускаемой относительной погрешности постоянен во всем диапазоне измерений и его определяют по формуле (6):

, (6)
где Х – результат измерения;

– инструментальная погрешность.

Выразим из формулы (6) инструментальную погрешность:
. (7)
Ом.
Погрешность результата измерения определим по формуле:
, (8)
где – случайная составляющая погрешности измерений (согласно заданию 1 =2,0396 Ом),
Ом.
Результат измерения (с учётом правил округления):
Ом.
3. Для обработки результатов косвенных измерений (таблица 3) необходимо определить:

а) истинное значение измеряемой величины;

б) абсолютную погрешность результата измерения;

в) относительную погрешность измерения.

Записать результат с учетом правила округления.
Таблица 3 – Косвенные измерения

№ вар	Измеряемая величина	Известная величина
2	U	I=10 А, ΔI=0,01 А

Выполнение
Определим истинное значение напряжения по формуле:
, В, (9)
В.
Абсолютная погрешность косвенного измерения определяется следующим образом:
, (10)
где , – частные производные от функции по соответствующим величинам.

, – абсолютные погрешности результатов прямых измерений.

В данном случае погрешность будет равна:
. (11)
Определим частную производную (9) по I:
.
Определим частную производную (9) по R:
.
Тогда абсолютная погрешность косвенного измерения:
, (12)
В.
Относительную погрешность определяем по формуле (9):
%.
Запишем результат измерения с учётом правил округления:
, В.
Выводы: проведена обработка результатов прямых измерений, результат измерения Ом, =0,95. Вычислена инструментальная погрешность и погрешность измерения, результат измерения принял вид Ом.

Проведена обработка результатов косвенных измерений, результат измерения , В.