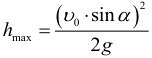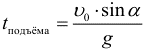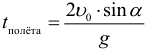БАЛЛИСТИЧЕСКОЕ ДВИЖЕНИЕ. баллистическое движение
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
ПРОЕКТ ПО ФИЗИКЕ НА ТЕМУ: «БАЛЛИСТИЧЕСКОЕ ДВИЖЕНИЕ» Содержание Введение…………………………………………………………………….3 Цель и задачи проекта 3 История возникновения баллистики 4 Теория баллистического движения………….………….………………...5 Практическая работа: изучение движения тела, брошенного под углом к горизонту на экспериментальной установке……………………….…..8 Экспериментальная установка……………………………………...8 Решаемая задача……………………………………………………10 Постановка задачи……………..……………………………….....10 Теоретическая часть выбранной физической и математической модели……………………………………………….……………...11 Выполнение работы………………………………………………..13 Определение начальной скорости снаряда……...……………13 Изучение зависимости дальности полета шарика-снаряда от угла наклона ствола пистолета………………..………………13 Исследование высоты подъема шарика-наряда……………...16 Влияние различной скорости на баллистическое движение..18 Заключение………………………………………………………………..19 Использованная литература………………………………….…………..20 Введение В многочисленных войнах на протяжении всей истории человечества враждующие стороны, доказывая своё превосходство, использовали сначала камни, копья, и стрелы, а затем ядра, пули, снаряды, и бомбы. Успех сражения во многом определялся точностью попадания в цель. При этом точный бросок камня, поражение противника летящим копьём или стрелой фиксировались воином визуально. Это позволяло при соответствующей тренировке повторять свой успех в следующем сражении. Значительно возросшая с развитием техники скорость и дальность полёта снарядов и пуль сделали возможным дистанционные сражения. Однако навыка воина, разрешающей способности его глаза было недостаточно для точного попадания в цель артиллерийской дуэли первым. Желание побеждать стимулировало появление баллистики. Цель и задачи проекта: изучение возникновения и развития баллистики как науки, изучение баллистического движения тела, брошенного под углом к горизонту; построение математической модели физического процесса движения тела, брошенного под углом к горизонту; построение экспериментальной установки для проведения экспериментов изучения баллистического движения тела, брошенного под углом к горизонту; на примере выполнения экспериментов выяснить зависимости дальности полета, формы траектории, высоты и времени полета тела от угла броска и начальной скорости, а также выполнить сравнение результатов экспериментов с физическими законами баллистического движения тела, брошенного под углом к горизонту; подтвердить корректность выбора математической модели физического процесса движения тела, брошенного под углом к горизонту, сделанные допущения и упрощения. Изучать особенности баллистического движения начали довольно таки давно, еще в XVI веке, это было связано с появлением и совершенствованием артиллерийских орудий. Рис.5. Траектория движения артиллерийского снаряда. Близко к правильному решению о полете пушечных ядер подошел итальянский математик Тарталья, он сумел показать, что наибольшей дальности полета снарядов можно достичь при направлении выстрела под углом 45° к горизонту. В его книге "Новая наука" были сформулированы правила стрельбы, которыми артиллеристы руководствовались до середины ХVII века. Однако, полное решение проблем, связанных с движением тел, брошенных горизонтально или под углом к горизонту, осуществил все тот же Галилей. В своих рассуждениях он исходил из двух основных идей: тела, движущиеся горизонтально и не подвергающиеся воздействию других сил будут сохранять свою скорость; появление внешних воздействий изменит скорость движущегося тела независимо от того, покоилось или двигалось оно до начала их действия. Галилей показал, что траектории снарядов, если пренебречь сопротивлением воздуха, представляют собой параболы. Галилей указывал, что при реальном движении снарядов, вследствие сопротивления воздуха, их траектория уже не будет напоминать параболу: нисходящая ветвь траектории будет идти несколько круче, чем расчетная кривая. Ньютон и другие ученые разрабатывали и совершенствовали новую теорию стрельбы, с учетом возросшего влияния на движение артиллерийских снарядов сил сопротивления воздуха. Появилась и новая наука – баллистика. В современной баллистике для решения подобных задач используется электронно-вычислительная техника - компьютеры, а мы пока ограничимся простым случаем - изучением такого движения, при котором сопротивлением воздуха можно пренебречь. Это позволит нам повторить рассуждения Галилея почти без всяких изменений. Теория баллистического движения Балли́стика (от греческого слова ballo - бросаю) — наука о законах полета тел, проходящих часть пути в пространстве как свободно брошенное тело, основанная на математике и физике. Она занимается, главным образом, исследованием движения пуль, снарядов и мин, выпущенных из огнестрельного оружия, а также ракетных снарядов и баллистических ракет. Движение тела, брошенного под углом к горизонту. 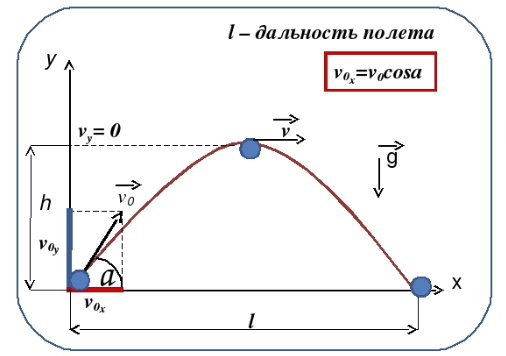 Рис.1. Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1). Проекции скорости тела, следовательно, изменяются со временем следующим образом: 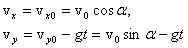 где Координаты тела, следовательно, изменяются так: 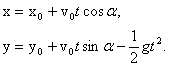 При нашем выборе начала координат начальные координаты
Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:
Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл. Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t0. Подставляя значение (2) в первую формулу (1), используя формулу тригонометрии
Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов. Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты хиу тела во время движения. Для этого нужно из первого уравнения (1) выразить время: 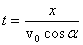 и подставить его во второе уравнение. Тогда получим: 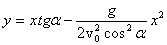 . .Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа. Практическая работа: изучение движения тела, брошенного под углом к горизонту на экспериментальной установке. Экспериментальная установка:  Рис.2.  Рис.3. Для экспериментального опыта проверки законов баллистического движения была собрана экспериментальная установка из: баллистического пистолета, представляющего собой спиральную пружину, помещенную в трубку-ствол, укрепленную в тисках (станина стреляющего орудия); измерительных приборов: измерительная линейка, нанесенная на горизонтальной поверхности стола, для измерения дальности полета снаряда в горизонтальном направлении; измерительная линейка для измерения высоты полета снаряда в вертикальном направлении; угломер баллистического пистолета – распечатанный лист с линейкой-транспортиром, центр которого размещен в точке вылета снаряда. В качестве снаряда были использованы пластмассовые шары массой 2 и 5 граммов. В ствол пистолета закладывается шарик-снаряд. Пружину пистолета сжимаем и зацепляем за спусковой крючок в основании ствола. При нажатии на спусковой крючок пружина освобождается и разжимается. Под действием разжимающейся пружины, шарик-снаряд двигается вдоль ствола пистолета в заданном направлении. На столе в месте падения шарика нанесена измерительная линейка с шагом 1 см. Место падения шарика на столе фиксируется с помощью смартфона видеосъемкой в замедленном режиме со скоростью съемки 960 кадров в секунду. Решаемая задача: Построим математическую модель физического процесса движения тела, брошенного под углом к горизонту. Выясним зависимость расстояния, траектории, высоты и времени полета тела от угла броска и начальной скорости. Сравним результаты экспериментов с физическими законами баллистического движения тела, брошенного под углом к горизонту. Постановка задачи: Для описания баллистического движения удобно вести идеальную модель, движущуюся с постоянным ускорением, пренебречь сопротивлением воздуха, вращением Земли. Начало системы координат расположено в точке бросания. Тело движется вблизи поверхности Земли, т. е. ускорение свободного падения постоянно и равно 9,81 м/с2. Сопротивление воздуха не учитывается, поэтому движение по горизонтали равномерное. Теоретическая часть выбранной физической и математической модели: Максимальная высота, на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
При стрельбе на горизонтальной поверхности под различными углами Движение снаряда описывается соотношениями: Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Полное время полета тела, брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Дальность полета снаряда выражается формулой:
Из этой формулы (9) следует, что при изменении угла вылета α снаряда от 900 до 00 дальность его падения максимальна, когда множитель sin2αнаибольшее. Синус имеет максимальное значение равное 1 при угле 900 . Следовательно, максимальная дальность будет при α = 450 . Эту зависимость в данной работе проверим на опыте с помощью баллистического пистолета. Убедимся, что максимальная дальность будет при стрельбе под углом α = 450, а для двух углов, дающих в сумме 900, дальность полета одинакова. Данная формула (9) выражает связь между дальностью полета и начальной скоростью снаряда. Если одну из этих величин мы определили экспериментально, то формула позволяет вторую величину вычислить: т.о. мы можем, стреляя из баллистического пистолета под разными углами α, измерять дальность полета снаряда l, а затем вычислить начальную скорость снаряда v0 по формуле (9). С другой стороны, если выстрел производится в вертикальном направлении, то, измеряя высоту подъема снаряда Н, можно определить начальную скорость из соотношения:
Начальная скорость зависит только от упругости пружины пистолета, массы шарика и других параметров прибора. При разных углах наклона ствола меняется только направление скорости, но не ее величина. Если величина начальной скорости v0 снаряда известна, было бы интересно убедиться в верности полученных формул. Выполнение работы: Определение начальной скорости снаряда. Установим пистолет в положении вертикально вверх (угол α = 900). Рядом с пистолетом ставим вертикально линейку так, чтобы начало отсчета совпадало с центром снаряда (масса шарика-снаряда в эксперименте 2 грамма). Делаем несколько выстрелов, записывая в таблицу высоту полета шарика. Находим среднюю высоту, и вычисляем начальную скорость снаряда по формуле (10):
Таблица 1. Т.о. пружина выталкивает шарик массой 8 грамм на среднюю высоту H(max)=26 см, из чего мы по формуле (10) получаем среднюю начальную скорость v0 = 2.26 м/с. Для шарика массой 5 грамм: средняя высота H(max)=32см и средняя начальная скорость v0 = 2.51 м/с. Для шарика массой 2 грамма: средняя высота H(max)=26см и средняя начальная скорость v0 = 3.04м/с. Изучение зависимости дальности полета шарика-снаряда от угла наклона ствола пистолета. Устанавливаем пистолет под углами 100, 200, 300, 400, 450, 500, 600, 700, 800 и делаем несколько выстрелов для каждого угла. Фиксируем дальность полета каждого шарика-снаряда (2, 5 и 8 грамм). Среднее значение дальности полета для каждого угла и шарика записываем в таблицу результатов измерений. По формуле (9) вычисляем расчетное значение дальности полета для каждого угла и шарика также записываем в таблицу результатов измерений. Вариант А: Шарик массой 8 грамм, с начальной скоростью v0 = 2.26 м/с:
Таблица 2. Вариант B: Шарик массой 5 грамм, с начальной скоростью v0 = 2.51 м/с:
Таблица 3. Вариант C: Шарик массой 2 грамм, с начальной скоростью v0 = 3.04 м/с:
Таблица 4. По данным таблиц 2, 3 и 4 построим графики дальности полета шариков в зависимости от угла выстрела: 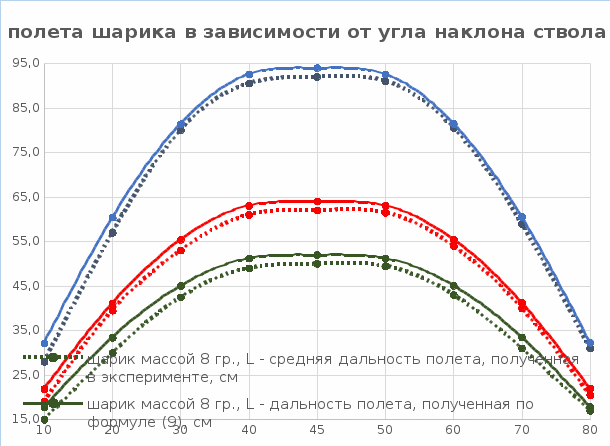 Рис. 4 Выводы, которые можно сделать при исследовании зависимости дальности полета снаряда при разных углах наклона пистолета для шариков: Дальность полета шарика-снаряда, вылетевшего из баллистического пистолета под углом к горизонту, зависит от величины начальной скорости и угла бросания. Чем выше начальная скорость, тем больше дальность полета. При неизменной скорости бросания v0, с увеличением угла, между направлением скорости бросания и горизонтальной поверхностью от 0 до 45°, дальность полета возрастает, а при дальнейшем росте угла бросания – уменьшается. Максимальная дальность полета при данной скорости вылета достигается при угле бросания 45°. Значит, наиболее «выгодным» для дальнего броска является угол в 45°, при любых других значениях угла бросания дальность полета будет меньше. Зависимость дальности полета от угла выстрела имеет параболический вид и для любых двух углов выстрела, сумма углов которых составляет 90° (например, 30° и 60°), дальность полета одинакова. Экспериментальная дальность полета шариков оказалась несколько меньше, чем расчетная дальность полета по формуле (9). Это объясняется прежде всего из-за влияния силы трения в поршне ствола баллистического пистолета, которое в расчетах не учитывалось. Можно сделать вывод, что выбранная математическая модель физического процесса движения тела, брошенного под углом к горизонту достаточно корректно описывает результаты «метаний» шариков-снарядов, полученные на экспериментальной установке. А сделанные допущения и упрощения дают несущественные отклонения полученных результатов в ходе экспериментов от расчетных значений по формулам баллистического движения. Для более точных результатов необходимо дополнительно учесть в математической модели влияние силы трения поршня в стволе баллистического пистолета и сопротивления воздуха во время полета снаряда. Исследование высоты подъема шарика-снаряда. На примере одного шарика-снаряда, который выбрасывается пружиной пистолета с начальной скоростью v0 = 2.26 м/с, вычислим максимальную высоту подъема и расстояние по горизонтали от точки выстрела до проекции точки траектории в которой шарик-снаряд находится в наивысшей точке на ось Х, используя полученные ранее результаты. Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Расстояние по горизонтали от точки выстрела до проекции точки траектории в которой шарик-снаряд находится в наивысшей точке на ось Х – это половина расстояния дальности полета по оси Х. Заполним таблицу:
Таблица 5. Проверим в ходе следующего эксперимента, что вычисленные значения высоты полета снаряда соответствуют реальности. Для этого на половине дальности полета шарика от точки вылета для данного угла наклона пистолета по траектории полета шарика в вертикальной плоскости кольцо на вычисленной высоте из Таблицы 5. Производим выстрелы. Опыты показывают, что расчет были сделаны правильно – шарик-снаряд пролетает сквозь кольцо и поражает экспериментальную мишень. 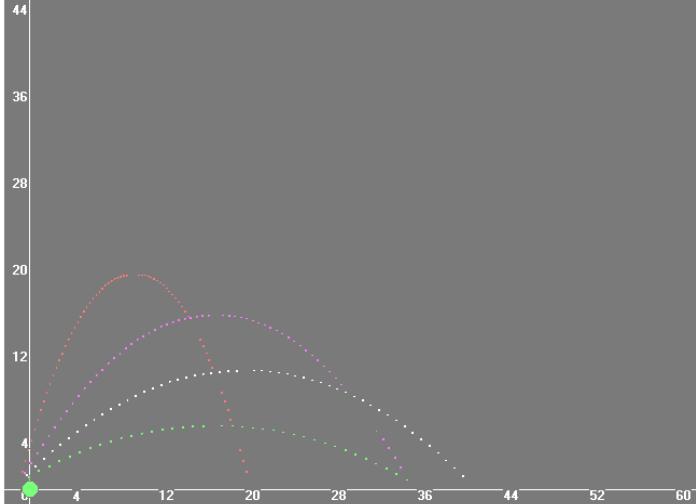 Рис. 5. На рисунке 5 изображены траектории шарика-снаряда с начальной скоростью v0 = 2.26 м/с: зеленым цветом выпущенного под углом 30°, белым -под углом 40°, фиолетовым - под углом 50°, а красным - под углом 60°. А теперь посмотрим на графики полёта снарядов и сравним их. Вывод, который можно сделать при сравнении этих траекторий полёта шарика-снаряда: с увеличением угла вылета снаряда, при одинаковой начальной скорости, дальность полёта уменьшается, а высота увеличивается. 5.5.4. Влияние различной скорости на баллистическое движение. Рассмотрим случай на примере полученных результатов с выстрелами разными шариками-снарядами, связанный с различной начальной скоростью данных шариков-снарядов, при одинаковом угле вылета. На рисунке 6 разными цветами схематично показаны траектории полета каждого из использованных в эксперименте шариков-снарядов при одинаковом угле вылета α = 200: зеленым цветом изображен график шарика-снаряда выпущенного с начальной скоростью 2,26 м/с, белым - со скоростью 2,51 м/с, фиолетовым - со скоростью 3,04 м/с. 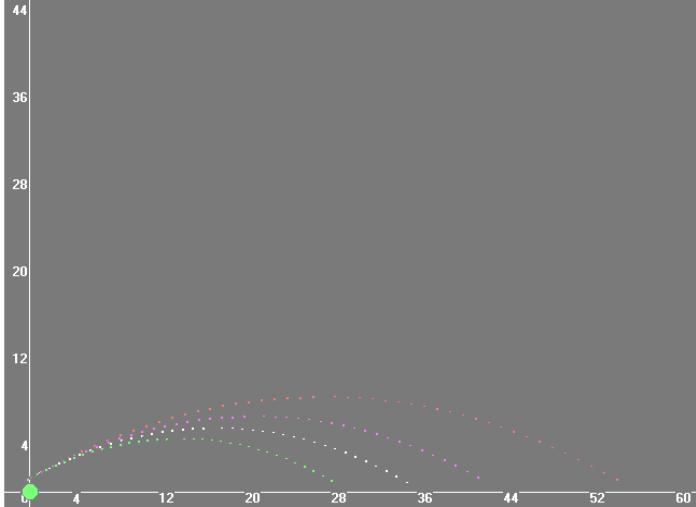 Рис. 6. Вывод, который можно сделать при сравнении этих траекторий полёта шариков-снарядов: с увеличением начальной скорости вылета снаряда, при одинаковом угле вылета, дальность и высота полёта снаряда увеличиваются. Заключение В результате выполнения проекта было изучено возникновение и развитие баллистики как науки, изучение баллистического движения тела, брошенного под углом к горизонту. Была выбрана математическая модель физического процесса движения тела, брошенного под углом к горизонту, которая достаточно корректно описывает баллистическое движение шариков-снарядов в подготовленной экспериментальной установке. Построена экспериментальная установка для проведения экспериментов для изучения баллистического движения тела, брошенного под углом к горизонту. По результатам выполнения экспериментов на экспериментальной установке: были выяснены зависимости дальности полета, формы траектории, высоты и времени полета тела от угла броска и начальной скорости, а также выполнено сравнение результатов экспериментов с физическими законами баллистического движения тела, брошенного под углом к горизонту; была подтверждена корректность выбора математической модели физического процесса движения тела, брошенного под углом к горизонту, сделанные допущения и упрощения; было отмечено, что необходимо дополнительно учесть в математической модели для большей точности расчета баллистики тела. Использованная литература: Учебник «Физика – 10», автор В.А. Касьянов, издательство Дрофа, 2019. Физический энциклопедический словарь [Электронный ресурс]. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. — 1983. Баллистика [Электронный ресурс]. — Википедия – свободная энциклопедия. https://ru.wikipedia.org/wiki/%D0%91%D0%B0%D0%BB%D0%BB%D0%B8%D1%81%D1%82%D0%B8%D0%BA%D0%B0 Полет снаряда [Электронный ресурс]. — Википедия – свободная энциклопедия. https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BB%D1%91%D1%82_%D1%81%D0%BD%D0%B0%D1%80%D1%8F%D0%B4%D0%B0 Зависимость формы траектории от угла бросания. Элементы траектории http://www.shooting-ua.com/books/book_111.2.htmБаллистика внешняя. [Электронный ресурс]. — Википедия – свободная энциклопедия. https://ru.wikisource.org/wiki/%D0%92%D0%AD/%D0%92%D0%A2/%D0%91%D0%B0%D0%BB%D0%B8%D1%81%D1%82%D0%B8%D0%BA%D0%B0_%D0%B2%D0%BD%D0%B5%D1%88%D0%BD%D1%8F%D1%8F |

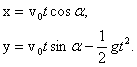
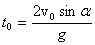 .
. .
.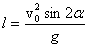
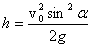 .
.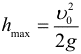 .
.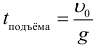
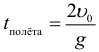 (5)
(5)