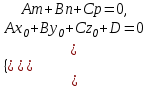Кеңістіктегі жазықтық теңдеуі_3лекция (2). Берілген нкте арылы тетін, берілген вектора перпендикуляр жазытыты тедеуі
 Скачать 1.53 Mb. Скачать 1.53 Mb.
|
|
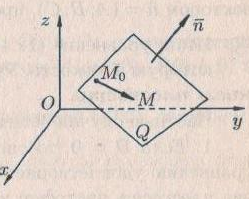
Кеңістіктегі жазықтық теңдеуі Қарапайым беттердің бір түрі жазықтық.  кеңістіктегі жазықтықты әр түрлі түрде беруге болады. Олардың әрқайсысына сәйкес теңдеулері болады. кеңістіктегі жазықтықты әр түрлі түрде беруге болады. Олардың әрқайсысына сәйкес теңдеулері болады.Берілген нүкте арқылы өтетін, берілген векторға перпендикуляр жазықтықтың теңдеуі.  кеңістігінде кеңістігінде  жазықтығы жазықтығы 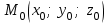 нүктесімен және осы жазықтыққа перпендикуляр нүктесімен және осы жазықтыққа перпендикуляр 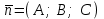 векторымен берілген. векторымен берілген. 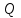 жазықтығының теңдеуін қорытып шығарайық. Жазықтықтан кез-келген жазықтығының теңдеуін қорытып шығарайық. Жазықтықтан кез-келген 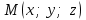 нүктесін алайық және нүктесін алайық және 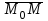 векторын құрайық. векторын құрайық.
М нүктесі 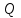 жазықтығында қалай орналассада жазықтығында қалай орналассада 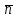 және және 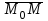 векторлары өзара перпендикуляр болады, сондықтан олардың скаляр көбейтіндісі нөлге тең: векторлары өзара перпендикуляр болады, сондықтан олардың скаляр көбейтіндісі нөлге тең: 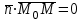 , яғни , яғни
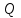 жазықтығының кез-келген нүктесі (1) теңдеуін қанағаттандырады, ал жазықтығының кез-келген нүктесі (1) теңдеуін қанағаттандырады, ал 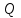 жазықтығында жатпайтын нүктелер қанағаттандырмайды. (олар үшін жазықтығында жатпайтын нүктелер қанағаттандырмайды. (олар үшін 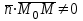 ), яғни ), яғни 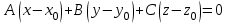 . .(1) теңдеу берілген. 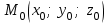 нүктесі арқылы өтетін, нүктесі арқылы өтетін, 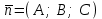 нормаль векторына перпендикуляр жазықтықтың теңдеуі деп аталады. нормаль векторына перпендикуляр жазықтықтың теңдеуі деп аталады. 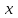 , , 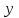 , және , және 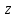 координаталарына байланысты жазықтықтың теңдеуі бірінші дәрежелі болады. координаталарына байланысты жазықтықтың теңдеуі бірінші дәрежелі болады. 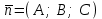 векторы жазықтықтың нормаль векторы деп аталады. векторы жазықтықтың нормаль векторы деп аталады. Жазықтықтың жалпы теңдеуі 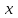 , , 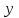 , және , және 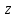 үш белгісізді бірінші дәрежелі теңдеуді қарастырайық: үш белгісізді бірінші дәрежелі теңдеуді қарастырайық:
Осы теңдеуді 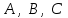 коэффициенттерінің бірдей нөлге тең емес болсын, мысалы, коэффициенттерінің бірдей нөлге тең емес болсын, мысалы, 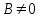 , онда (2) теңдеуін былайша жазуға болады: , онда (2) теңдеуін былайша жазуға болады:
(3) және (2) теңдеулерін салыстырып, біз (2) және (3) теңдеулері 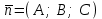 нормаль векторы бар. нормаль векторы бар. 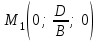 нүктесі арқылы өтетін жазықтықтың теңдеулері екенін көрініп тұр. нүктесі арқылы өтетін жазықтықтың теңдеулері екенін көрініп тұр.(2) теңдеуі 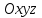 координаталар жүйесіндегі қандай да бір жазықтықты анықтайды. (2) теңдеуі жазықтықтың жалпы теңдеуі деп аталады. координаталар жүйесіндегі қандай да бір жазықтықты анықтайды. (2) теңдеуі жазықтықтың жалпы теңдеуі деп аталады. Жазықтықтың жалпы теңдеуінің дербес жағдайы Егер  болса, онда жазықтық болса, онда жазықтық 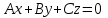 түрінде болады. Бұл түрінде болады. Бұл теңдеуді 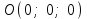 нүктесі қанағаттандырады. Демек бұл жағдайда жазықтық координаталардың бас нүктесі арқылы өтеді. нүктесі қанағаттандырады. Демек бұл жағдайда жазықтық координаталардың бас нүктесі арқылы өтеді. Егер 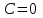 болса, онда жазықтық болса, онда жазықтық 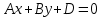 . . 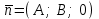 нормаль нормаль векторы 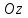 осіне перпендикуляр болады. Демек, жазықтық осіне перпендикуляр болады. Демек, жазықтық 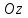 осіне параллель; егер осіне параллель; егер 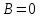 болса, онда болса, онда 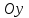 осіне параллель; егер осіне параллель; егер 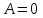 болса, онда болса, онда 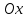 осіне параллель болады. осіне параллель болады. 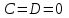 болса, онда жазықтық болса, онда жазықтық 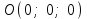 нүктесі арқылы өтіп нүктесі арқылы өтіп 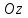 жазықтығына параллель болады, яғни 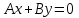 жазықтығы жазықтығы 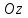 осі арқылы өтеді. Тура осылайша осі арқылы өтеді. Тура осылайша 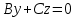 және және 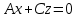 жазықтықтары сәйкес жазықтықтары сәйкес 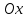 және және 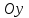 осьтері арқылы өтеді. осьтері арқылы өтеді.Егер 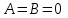 онда, (2) теңдеуі онда, (2) теңдеуі 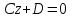 түріне келеді, яғни түріне келеді, яғни 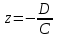 . . Бұл 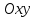 жазықтығына параллель жазықтық. Тура осылайша, жазықтығына параллель жазықтық. Тура осылайша, 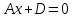 және және 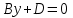 жазықтықтары сәйкес, жазықтықтары сәйкес,  және және  жазықтықтарына параллель жазықтықтарды анықтайды. жазықтықтарына параллель жазықтықтарды анықтайды. 5. 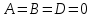 болса, онда (2) теңдеуі болса, онда (2) теңдеуі 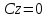 түріне келеді, яғни түріне келеді, яғни 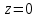 . . Бұл 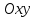 жазықтығының теңдеуі. Тура осылайша, жазықтығының теңдеуі. Тура осылайша, 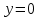 - - 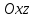 жазықтығының теңдеуі, жазықтығының теңдеуі, 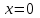 - -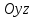 жазықтығының теңдеуі. жазықтығының теңдеуі.Берілген үш нүкте арқылы өтетін жазықтықтың теңдеуі Кеңістікте бір түзудің бойында жататын үш нүкте бір ғана жазықтықты анықтайды. Бір түзуде жатпайтын 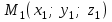 , , 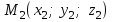 және және 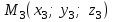 нүктелері арқылы өтетін нүктелері арқылы өтетін 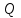 жазықтығының теңдеуін табайық. жазықтығының теңдеуін табайық.Жазықтықтан қалауымызша кез-келген 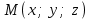 нүктесін алайық және нүктесін алайық және 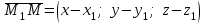 , , 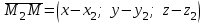 , , 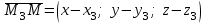 векторларын құрайық. Бұл векторлар векторларын құрайық. Бұл векторлар 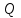 жазықтығында жатады, олар компланарлы векторлар. Векторлардың компланар шартын қолданып (олардың аралас көбейтіндісі нөлге тең), жазықтығында жатады, олар компланарлы векторлар. Векторлардың компланар шартын қолданып (олардың аралас көбейтіндісі нөлге тең), 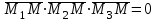 , аламыз, яғни , аламыз, яғни
(4) теңдеуі берілген үш нүкте арқылы өтетін жазықтықтың теңдеуі. Жазықтықтың кесінділер арқылы берілген теңдеуі Жазықтық 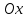 , , 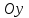 және және 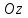 осьтерін осьтерін 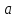 , , 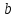 және және 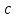 кесінділерін қияды, яғни ол кесінділерін қияды, яғни ол 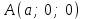 , , 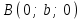 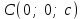 нүктелері арқылы өтеді. нүктелері арқылы өтеді. Осы нүктелердің координаталарын (4) теңдеуіне қойып, келесі анықтауышты аламыз
Анықтауышты ашып 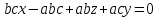 аламыз, яғни аламыз, яғни 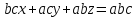 немесе немесе
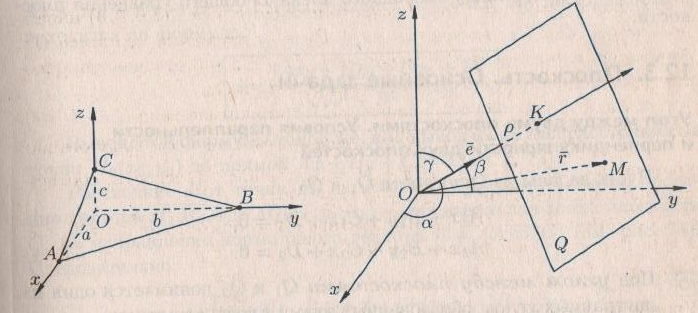
(5) теңдеуі координаталар осьтеріндегі жазықтық кесінділер бойынша теңдеуі деп аталады. Бұл теңдеу жазықтықтарды салғанда қолданған ыңғайлы. Жазықтықтың нормаль теңдеуі ОК=р болсын, болсын онда 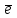 бірлік векторының бірлік векторының 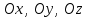 остерімен жасайтын бұрыштары остерімен жасайтын бұрыштары 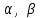 және және 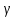 болады. Онда болады. Онда 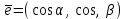 жазықтықпен кез-келген жазықтықпен кез-келген 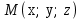 нүктесін алып, оны координаталар басымен қосайық. Сонда нүктесін алып, оны координаталар басымен қосайық. Сонда 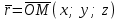 векторын аламыз: векторын аламыз:
(6) –теңдеуі векторлық формадағы жазықтықтың нормаль теңдеуі деп аталады. 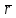 және және 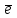 векторларының координаталары белгісіз, (7) теңдеуін векторларының координаталары белгісіз, (7) теңдеуін
(7) теңдеуі координаталық формадағы жазықтықтың нормаль теңдеуі. (2) жазықтықтың жалпы теңдеуін (7) нормалдық теңдеуіне келтіруге болады, яғни (2) теңдеудің екі жағында нормалдық теңдеу 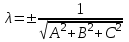 нормалдық көбейткішке көбейтеміз, мұндағы таңбасы жазықтықтың жалпы теңдеуінің нормалдық көбейткішке көбейтеміз, мұндағы таңбасы жазықтықтың жалпы теңдеуінің 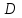 бос мүшесінің қарама-қарсы таңбасы алынады. бос мүшесінің қарама-қарсы таңбасы алынады. Жазықтықтар. Негізгі есептері Екі жазықтық арасындағы бұрыш. Екі жазықтықтың параллель және перпендикуляр болу шарттары 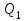 және және 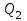 жазықтығы берілсін. жазықтығы берілсін.
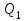 және және 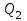 жазықтықтарының арасындағы бұрыш осы жазықтықтарынан құралған екі жақты бұрыш ұғымымен түсіндіріледі. жазықтықтарының арасындағы бұрыш осы жазықтықтарынан құралған екі жақты бұрыш ұғымымен түсіндіріледі. 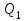 және және 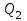 жазықтықтарының арасындағы бұрыш, осы жазықтықтардың жазықтықтарының арасындағы бұрыш, осы жазықтықтардың 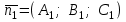 және және 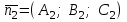 нормаль векторларының арасындағы бұрышқа тең. Сондықтан нормаль векторларының арасындағы бұрышқа тең. Сондықтан 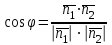 немесе немесе
Сүйір бұрышты табу үшін осы теңдіктің оң жағын модульге аламыз. Егер 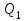 және және 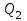 жазықтықтары перпендикуляр болса (73, а суретті қара), онда олардың нормаль векторлары перпендикуляр болады, яғни жазықтықтары перпендикуляр болса (73, а суретті қара), онда олардың нормаль векторлары перпендикуляр болады, яғни 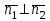 (және керісінше). Онда (және керісінше). Онда 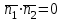 , ,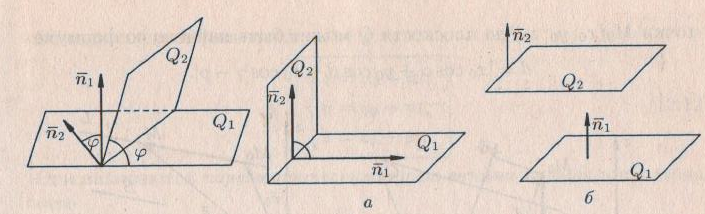
яғни 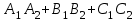 . Бұл теңдік екі . Бұл теңдік екі 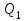 және және 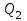 жазықтықтарының перпендикуляр болу шарты. жазықтықтарының перпендикуляр болу шарты. Егер 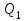 және және 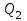 жазықтықтары параллель болса, онда олардың жазықтықтары параллель болса, онда олардың 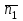 және және 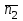 нормаль векторлары параллель болады. Онда олардың координаталары пропоционал болады: нормаль векторлары параллель болады. Онда олардың координаталары пропоционал болады: 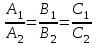 . Бұл . Бұл 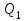 және және 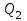 жазықтықтарының параллель болу шарты. жазықтықтарының параллель болу шарты. Нүктеден жазықтыққа дейінгі қашықтық. 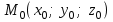 нүктесі мен нүктесі мен 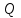 жазықтығы жазықтығы 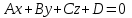 теңдеуімен берілсін. теңдеуімен берілсін. 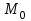 нүктесінен нүктесінен 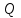 жазықтығына дейінгі жазықтығына дейінгі 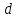 арақашықтығы келесі формула арқылы анықталады арақашықтығы келесі формула арқылы анықталады
Кеңістіктегі түзудің теңдеулері Түзудің векторлық теңдеуі Кеңістіктегі түзудің теңдеуі. Түзудің кез-келген 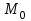 нүктесі және осы нүктесі және осы түзуге параллель 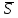 векторымен анықталады. векторымен анықталады. 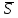 векторы түзудің бағыттауыш векторы деп аталады. векторы түзудің бағыттауыш векторы деп аталады. 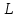 түзуі өзінің түзуі өзінің 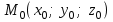 нүктесімен және нүктесімен және 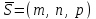 бағыттауыш векторымен берілсін. Түзудің бойынан кез-келген бағыттауыш векторымен берілсін. Түзудің бойынан кез-келген 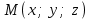 нүктесін белгілеп алайық. нүктесін белгілеп алайық. 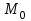 және және 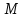 нүктелерінің радиус векторларын нүктелерінің радиус векторларын 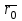 және және 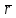 арқылы белгілейік. арқылы белгілейік. 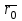 , , 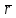 , , 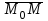 үш векторы үш векторы
қатынасымен байланысты. 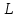 түзуінің бойында жатқан түзуінің бойында жатқан 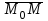 векторы векторы 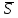 бағыттауыш векторына параллель, сондықтан бағыттауыш векторына параллель, сондықтан 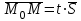 , мұндағы , мұндағы 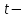 параметр деп аталатын скалярлық көбейткіш, ол түзудің М нүктесінен тәуелді әр түрлі мәндер қабылдайды. параметр деп аталатын скалярлық көбейткіш, ол түзудің М нүктесінен тәуелді әр түрлі мәндер қабылдайды. (2) формуласын
түрінде жазуға болады. Бұл шыққан теңдеуді түзудің векторлық теңдеуі деп аталады. Түзудің параметрлік теңдеуі 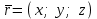 , , 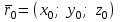 , , 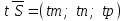 ескере отырып (2) теңдеуін ескере отырып (2) теңдеуін
түрінде жазуға болады. Бұдан
теңдігі шығады. Бұл теңдеуді түзудің параметрлік теңдеуі деп атайды. Түзудің канондық теңдеуі 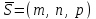 векторы векторы 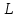 түзуінің бағытауыш векторы, ал түзуінің бағытауыш векторы, ал 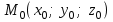 нүктесі осы түзуде жататын нүктесі. нүктесі осы түзуде жататын нүктесі. 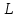 түзуінің бойындағы түзуінің бойындағы 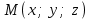 нүктесін нүктесін 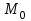 нүктесімен қосып, нүктесімен қосып, 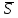 векторына параллель векторына параллель 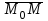 векторын жүргіземіз. Сондықтан, векторын жүргіземіз. Сондықтан, 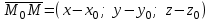 және және 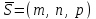 пропорционал болады: пропорционал болады:
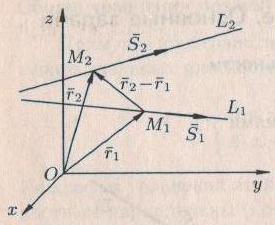
(4) теңдеуі түзудің канондық теңдеуі деп аталады. Екі нүкте арқылы өтетін кеңістіктегі түзудің теңдеуі 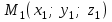 және және 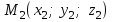 нүктелері арқылы өтетін нүктелері арқылы өтетін 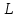 түзуі берілсін. Бағыттауыш түзуі берілсін. Бағыттауыш 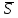 векторы ретінде векторы ретінде 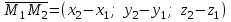 векторын алуға болады, яғни векторын алуға болады, яғни 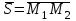 Демек, Демек, 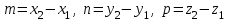 . Түзу . Түзу 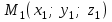 нүктесі арқылы өтетін болғандықтан, (4) теңдеуі бойынша, нүктесі арқылы өтетін болғандықтан, (4) теңдеуі бойынша,  түзуінің теңдеуі келесі түрде болады түзуінің теңдеуі келесі түрде болады
(5) теңдеуі берілген екі нүкте арқылы өтетін түзудің теңдеуі деп аталады. 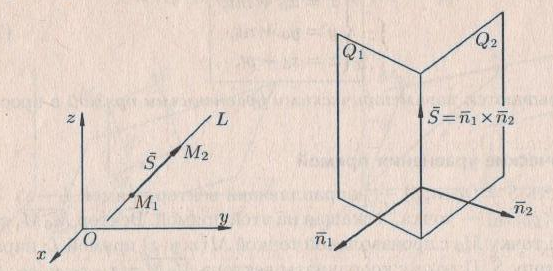 Түзудің жалпы теңдеуі Кеңістіктегі түзудің теңдеуі параллель емес екі жазықтық қиылсықанда пайда болған сызық арқылы беріледі
теңдеулер жүйесін қарастырайық. Бұл жүйенің әрбір теңдеуі жазықтықты анықтайды. Егер жазықтықтар параллель емес болса ( 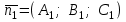 және және 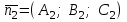 ) векторларының координаталары пропорционал болмайды.) онда (6) жүйесі, координаталары осы жүйенің әрбір теңдеуін қанағаттандыратын, кеңістіктегі геометриялық орны болатын ) векторларының координаталары пропорционал болмайды.) онда (6) жүйесі, координаталары осы жүйенің әрбір теңдеуін қанағаттандыратын, кеңістіктегі геометриялық орны болатын 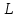 түзуін анықтайды. түзуін анықтайды. (6) жалпы теңдеуінен (5) канондық теңдеу түріне келтіруге болады. (12.15) жүйесіндегі теңдеулеріндегі координаталардың кез-келген біреуін нөлге теңестіріп, 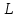 түзуінің түзуінің 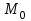 нүктесінің координаталарын табамыз (мысалы, нүктесінің координаталарын табамыз (мысалы, 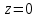 ). ). 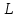 түзуі түзуі 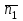 және және 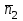 векторларына перпендикуляр болғандықтан, векторларына перпендикуляр болғандықтан, 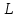 түзуінің түзуінің 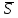 бағыттауыш векторы ретінде бағыттауыш векторы ретінде 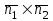 векторлық көбейтіндісін алуға болады: векторлық көбейтіндісін алуға болады:
Ескерту: Түзудің бойынан кез-келген екі нүктесін алып, (6) теңдеуін қолданып, түзудің канондық теңдеуін оңай шығарып алуға болады. мысал. 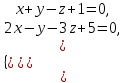 теңдеуімен берілген  түзуінің канондық теңдеуін жазу керек. түзуінің канондық теңдеуін жазу керек. Шешуі: 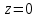 деп алып, деп алып, 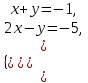 жүйесін шешеміз. жүйесін шешеміз. 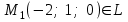 нүктесін табамыз. нүктесін табамыз. 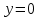 деп алып деп алып 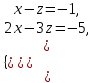 жүйесін шешеміз. жүйесін шешеміз. 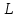 түзуінің түзуінің 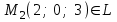 екінші нүктесін табамыз. екінші нүктесін табамыз. 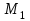 және және 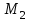 нүктелері арқылы өтетін нүктелері арқылы өтетін 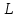 түзуінің теңдеуін жазамыз: түзуінің теңдеуін жазамыз: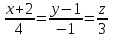 . .Кеңістіктегі түзу сызық. Негізгі есептер Түзулердің арасындағы бұрышы. Түзулердің параллель және перпендикуляр болу шарттары 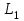 және және 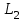 түзулері түзулері 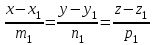 және және 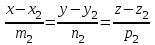 теңдеулерімен берілсін. теңдеулерімен берілсін.
косинусы формуласы бойынша келесі теңдеу 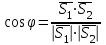 немесе немесе
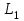 және және 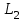 түзулерінің сүйір бұрышын табу үшін (12.16) теңдеуінің алымын модульмен алу керек. түзулерінің сүйір бұрышын табу үшін (12.16) теңдеуінің алымын модульмен алу керек. Егер 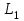 және және 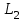 түзулері перпендикуляр болса, онда түзулері перпендикуляр болса, онда 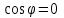 . Осыдан (7) бөлшегінің алымы нөлге тең, яғни . Осыдан (7) бөлшегінің алымы нөлге тең, яғни 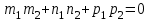 . .Егер 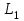 және және 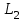 түзулері параллель болса, онда оның бағыттауыш түзулері параллель болса, онда оның бағыттауыш 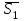 және және 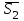 векторлары параллель болады. Демек, бұл векторлардың координаталары пропорционал болады, яғни векторлары параллель болады. Демек, бұл векторлардың координаталары пропорционал болады, яғни 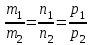 . .12.2-мысал. 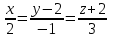 және және 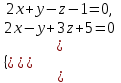 түзулері арасындағы бұрышты табу керек. түзулері арасындағы бұрышты табу керек. Шешуі: 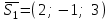 екені белгілі, ал екені белгілі, ал 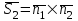 мұндағы мұндағы 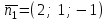 , , 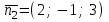 , бұдан , бұдан 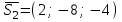 . . 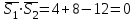 болғандықтан, болғандықтан, 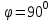 . . Екі түзудің бір жазықтықта жату шарты 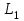 және және 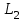 түзулері түзулері 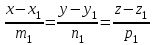 және және 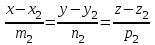 канондық теңдеуімен берілген. канондық теңдеуімен берілген.
Векторлардың компланарлы болу шарты бойынша, олардың аралас көбейтінділері нөлге тең болады: 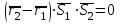 , яғни , яғни
Осы шарт орындалғанда 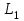 және және 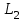 түзулері бір жазықтықта жатады, яғни қиылсады, егер түзулері бір жазықтықта жатады, яғни қиылсады, егер 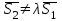 болса, ал параллель болады, егер болса, ал параллель болады, егер 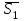 ║ ║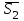 болса. болса. Кеңістіктегі түзу мен жазықтық Түзу мен жазықтықтың арасындағы бұрыш. Түзу мен жазықтықтың параллель, перпендикуляр болу шарты  жазықтығы жазықтығы 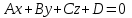 теңдеуімен теңдеуімен  түзуі түзуі  теңдеуімен берілсін. теңдеуімен берілсін. Түзу мен жазықтық арасындағы бұрышы деп, оның жазықтыққа түсірілген проекциясы мен түзудің арасындағы екі сыбайлас бұрыштың кез-келген біреуін айтады. 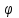 деп деп 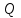 жазықтығы мен жазықтығы мен 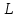 түзуі арасындағы бұрышты, ал түзуі арасындағы бұрышты, ал 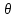 деп деп 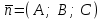 нормаль векторы мен нормаль векторы мен 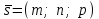 бағыттауыш векторы арасындағы бұрышты белгілейік. Сонда бағыттауыш векторы арасындағы бұрышты белгілейік. Сонда 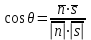 , , 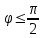 деп есептеп синус деп есептеп синус 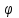 бұрышын табамыз. бұрышын табамыз. 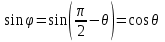 . . 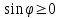 болғандықтан болғандықтан
Егер 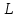 түзуі түзуі 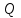 жазықтығына параллель болса, онда жазықтығына параллель болса, онда 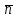 және және 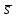 векторлары перпендикуляр болады, сондықтан векторлары перпендикуляр болады, сондықтан 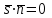 , яғни , яғни
Бұл түзу мен жазықтықтың параллель болу шарты. 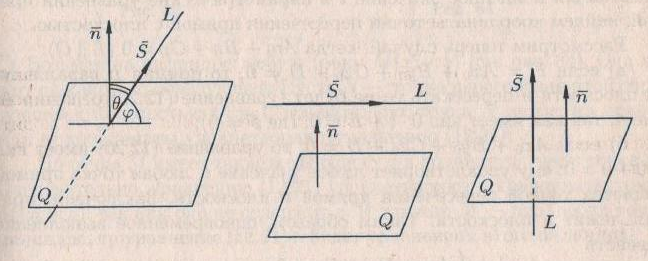 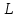 түзуі түзуі 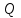 жазықтығына перпендикуляр болса, онда жазықтығына перпендикуляр болса, онда 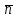 және және 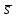 векторлар параллель болады Сондықтан векторлар параллель болады Сондықтан
түзу мен жазықтықтың перпендикуляр болу шарты. Түзудің жазықтықпен қиылсу шарты. Түзудің жазықтыққа тиісті болу шарты
түзуінің
жазықтығымен қиылсу нүктесін табу керек болсын. Ол үшін (11) және (10) теңдеулер жүйесін шешу керек. Ол үшін (11) түзудің теңдеуін параметрлік түрде жазамыз:
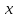 , , 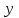 және және 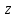 өрнектерінің мәндерін (10) жазықтықтың теңдеуіне қойып өрнектерінің мәндерін (10) жазықтықтың теңдеуіне қойып 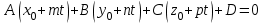 немесе немесе
теңдеуін аламыз. Егер 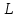 түзуі жазықтыққа параллель болмаса, яғни түзуі жазықтыққа параллель болмаса, яғни 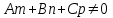 , онда (12) теңдеуінен , онда (12) теңдеуінен 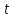 параметрін табамыз: параметрін табамыз:
Содан соң 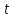 -ның табылған мәнін түзудің параметрлік теңдеуіне қойып, түзудің жазықтықпен қиылсу нүктесін табамыз. -ның табылған мәнін түзудің параметрлік теңдеуіне қойып, түзудің жазықтықпен қиылсу нүктесін табамыз. Енді 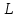 ║ ║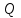 , яғни , яғни 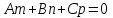 болған жағдайды қарастырамыз: болған жағдайды қарастырамыз:а) Егер 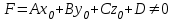 болса, онда болса, онда 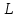 түзуі жазықтыққа парллель және қиылспайды (онда (12.20) теңдеуінің шешімі болмайды, яғни түзуі жазықтыққа парллель және қиылспайды (онда (12.20) теңдеуінің шешімі болмайды, яғни 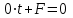 , мұндағы , мұндағы 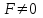 ). ).б) Егер 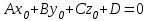 болса, онда (12) теңдеуі болса, онда (12) теңдеуі 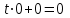 болады. болады. 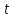 -ның кез-келген мәні оны қанағаттандырады және түзудің кез-келген мәні оны қанағаттандырады және түзудің кез-келген нүктесі түзу мен жазықтықтың қиылсу нүктесі болады. Онда түзу жазықтыққа тиісті деп қортындылаймыз. Осылайша, -ның кез-келген мәні оны қанағаттандырады және түзудің кез-келген мәні оны қанағаттандырады және түзудің кез-келген нүктесі түзу мен жазықтықтың қиылсу нүктесі болады. Онда түзу жазықтыққа тиісті деп қортындылаймыз. Осылайша,
теңдіктері орындалса, онда ол түзудің жазықтыққа тиісті болу шарты болады. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

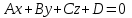 .
.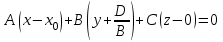 .
.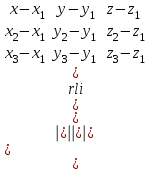 .
.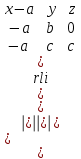 .
.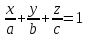 .
.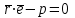 ,
,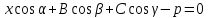 ,
,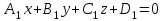 ,
,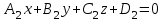 .
.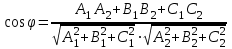 .
.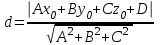 .
.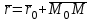 .
.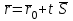 .
.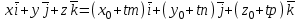 .
.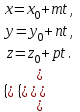
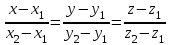 .
.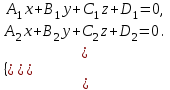 ,
,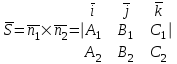 .
.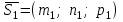 және
және 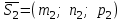 бағыттауыш векторларының арасындағы бұрышымен анықталады. (78 суретті қара). Сондықтан бұрын белгілі векторлардың арасындағы бұрыштың
бағыттауыш векторларының арасындағы бұрышымен анықталады. (78 суретті қара). Сондықтан бұрын белгілі векторлардың арасындағы бұрыштың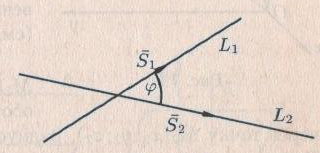
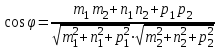 .
.
 ,
,  болып
болып  нүктесі арқылы өтетін
нүктесі арқылы өтетін 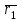 арқылы
арқылы 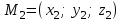 нүктесі арқылы өтетін
нүктесі арқылы өтетін 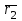 деп белгілейік. Онда
деп белгілейік. Онда 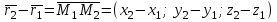 .
.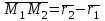 векторлары компланарлы болса.
векторлары компланарлы болса.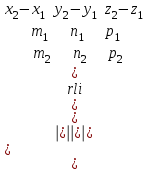 .
.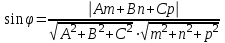 .
.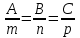
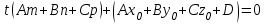
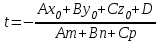 .
.