Бесконечные произведения. . Общие сведения def
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
РАЗДЕЛ 6. Бесконечные произведения. §. ОБЩИЕ СВЕДЕНИЯ Def: Конструкция вида Def: Если Def: Если Def: Если Рассмотрим Получили: необходимое условие сходимости бесконечного произведения: *. Если бесконечное произведение сходится, то его общий член стремится к единице. Примеры: 1. 2. Бесконечное произведение расходится, хотя *. Каждому бесконечному произведению Причём последовательность и произведение сходятся или расходятся одновременно (по определению), за исключением произведений расходящихся к нулю. §. Достаточное условие сходимости бесконечного произведения. Если ряды ∆ Т.к. Тогда Замечание: Существуют бесконечные произведения, для которых расходятся, но §. Связь между рядами и бесконечными произведениями. Записывая очевидное равенство: Def: Бесконечное произведение Примеры: 1. Рассмотрим = Бесконечное произведение сходится, по определению. 2. Рассмотрим Произведение сходится, если §. Разложение sin xи cos x в бесконечное произведение. Запишем формулу Муавра Отметим что при четных = т.е. Разложив 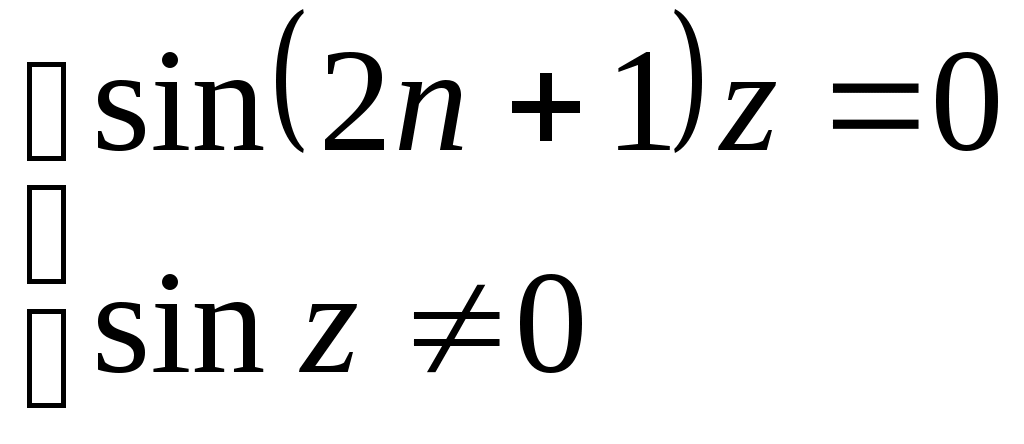 , то z -корень , то z -корень 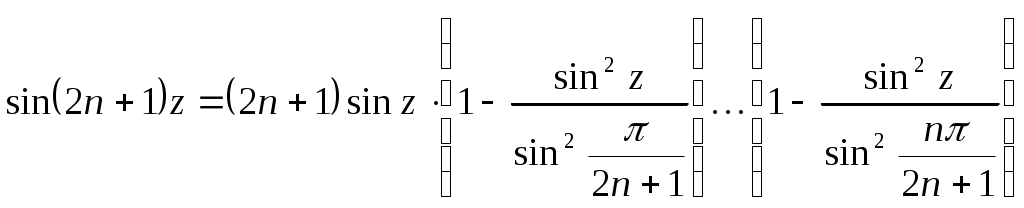 . .Положим 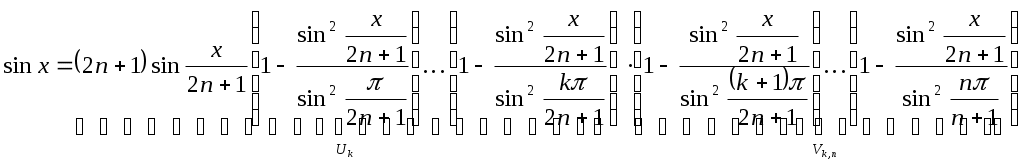 Тогда: 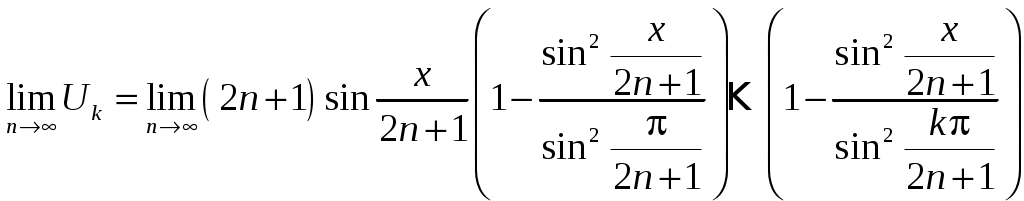 = = 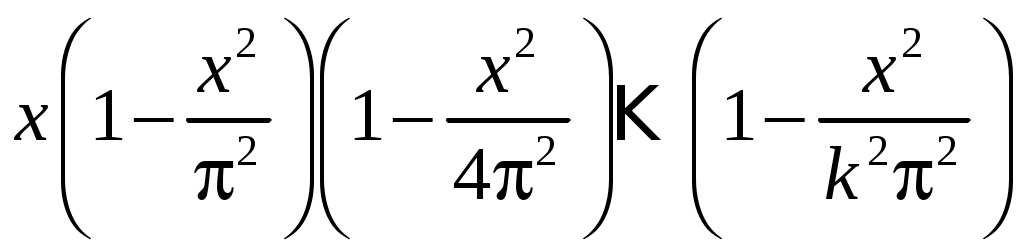 . .Чтобы рассмотреть Тогда: 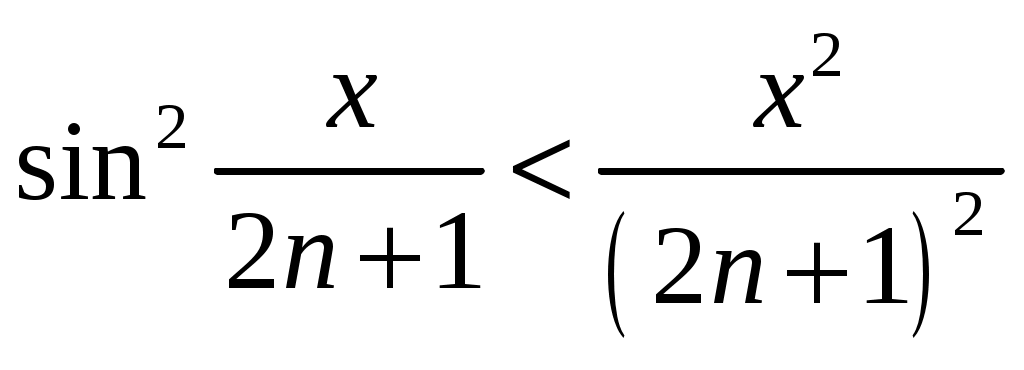 и и 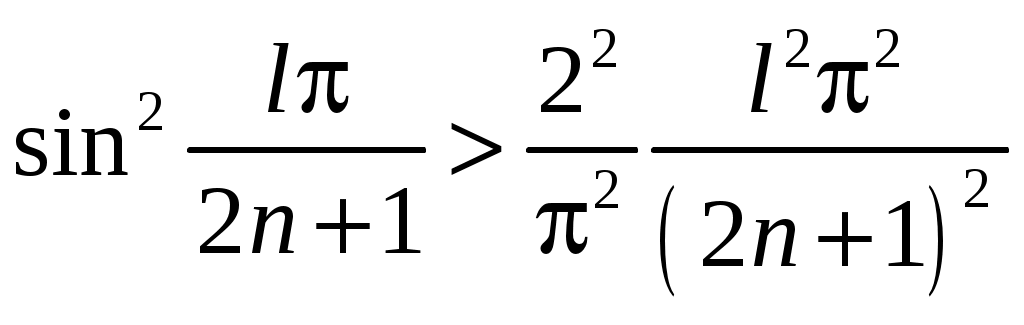 . .Следовательно: 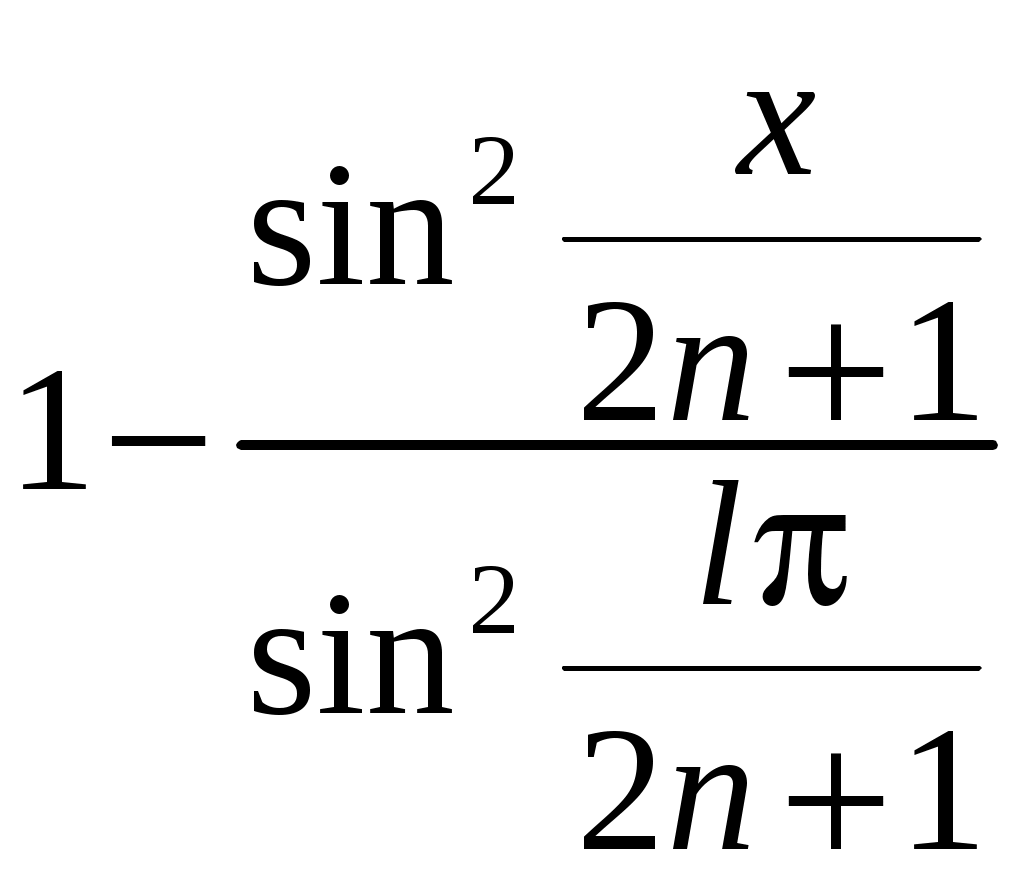 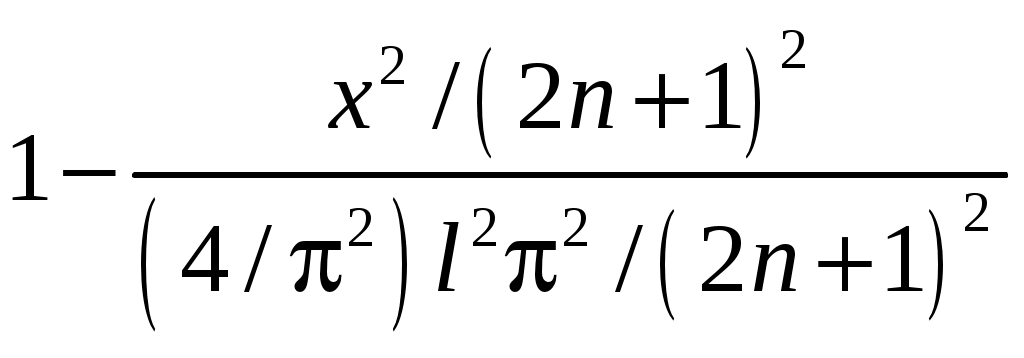 = = Таким образом: 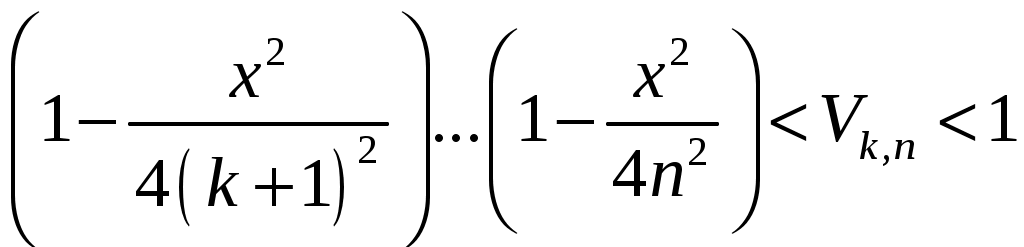 (*) (*)Бесконечное произведение 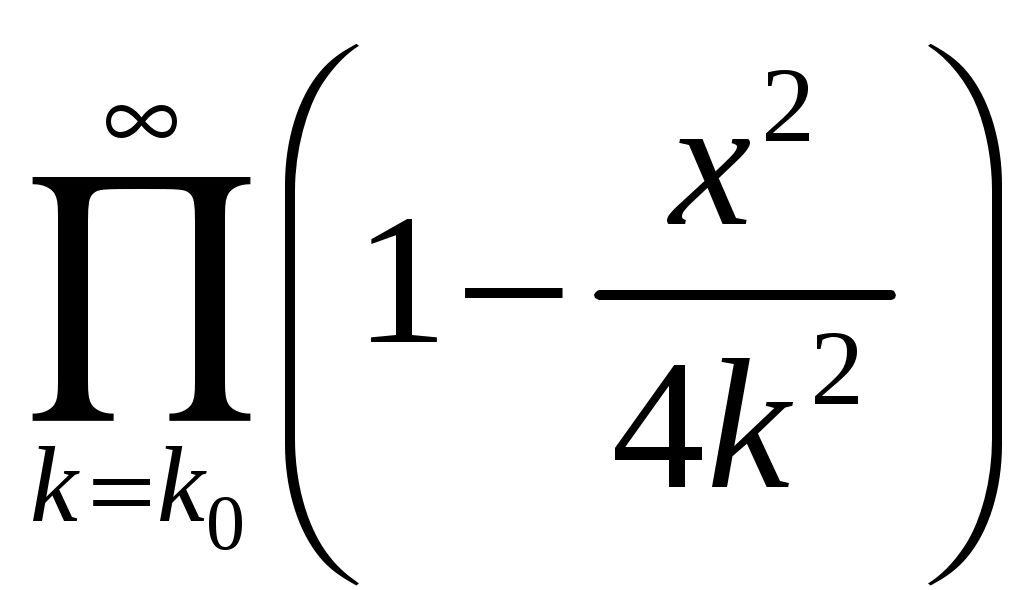 сходится, ибо сходится ряд сходится, ибо сходится ряд 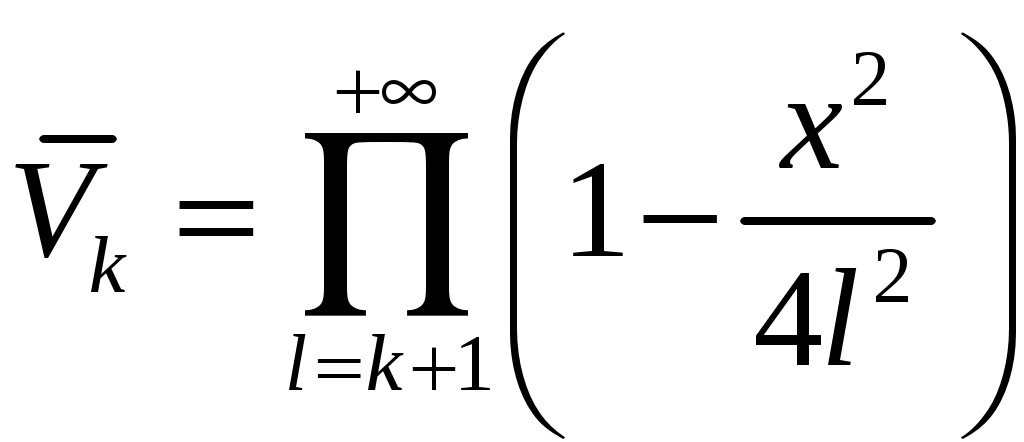 должно стремиться к единице при должно стремиться к единице при Переходя к пределу при Учитывая, что В самом деле 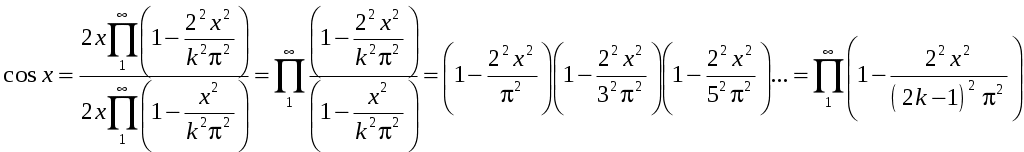 . .Тоже самое разложение можно получить и записав 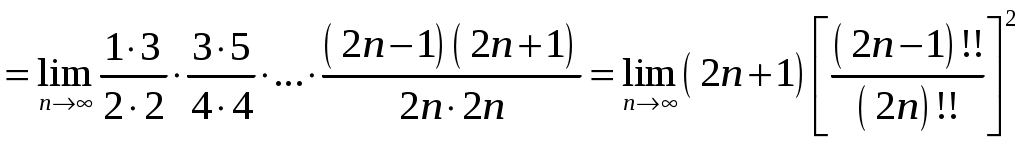 . .§. Формула Стирлинга. Запишем разложения : Положим в этой формуле 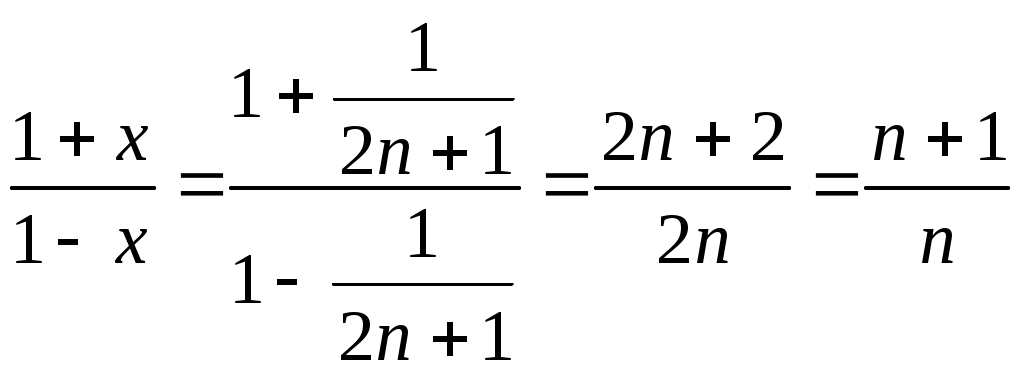 и, следовательно: и, следовательно: 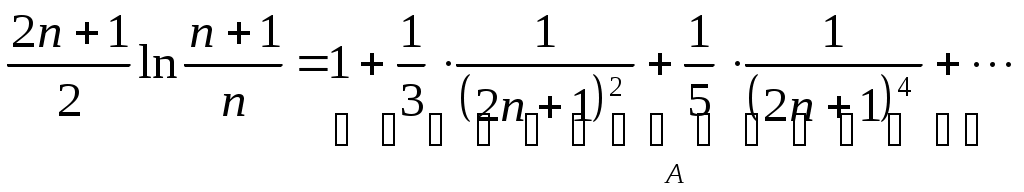 . И, очевидно, . И, очевидно, Оценка сверху для 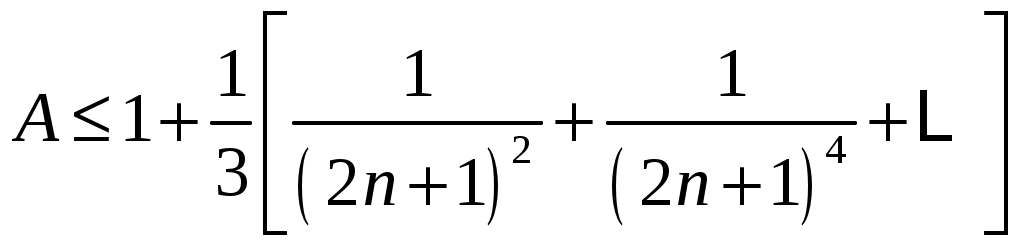 = = = Из оценок для Теперь рассмотрим последовательность: 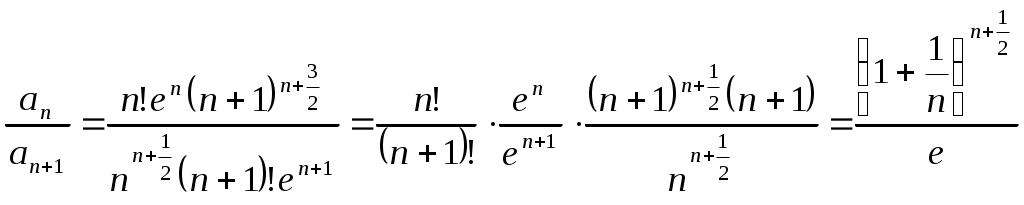 . .учитывая (*), получаем: 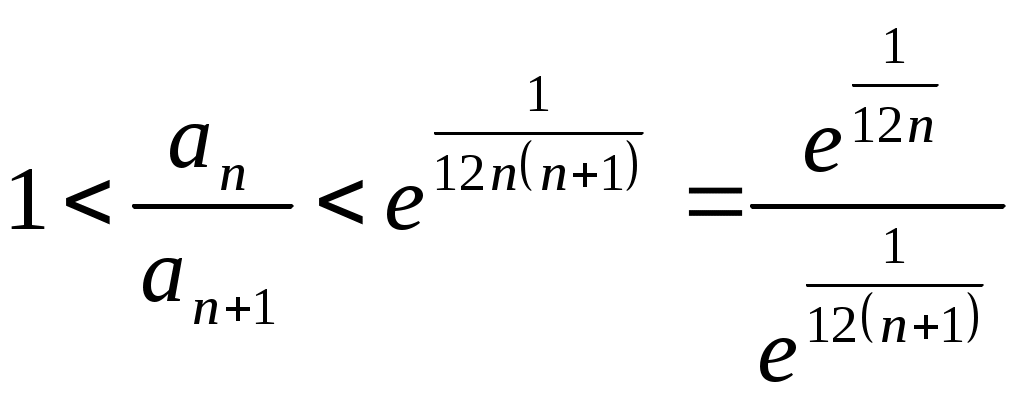 . .Таким образом: Последовательность Для нахождения величины a воспользуемся формулой Валлиса: 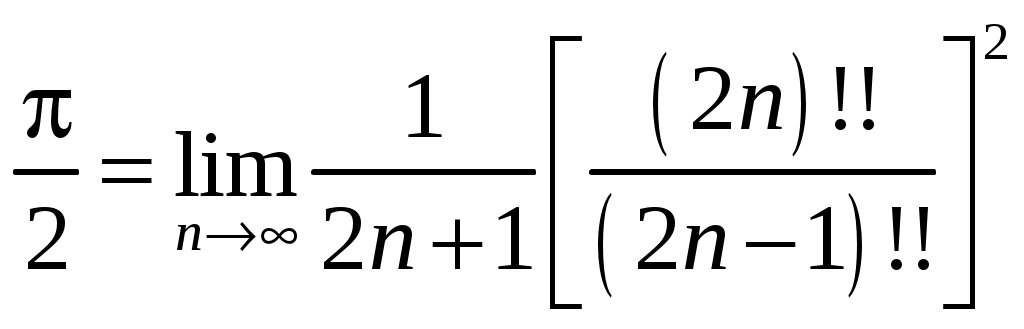 . .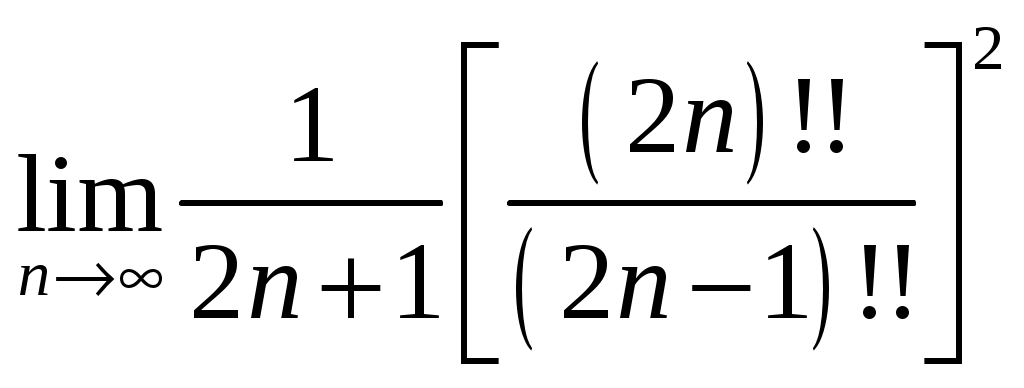 = = 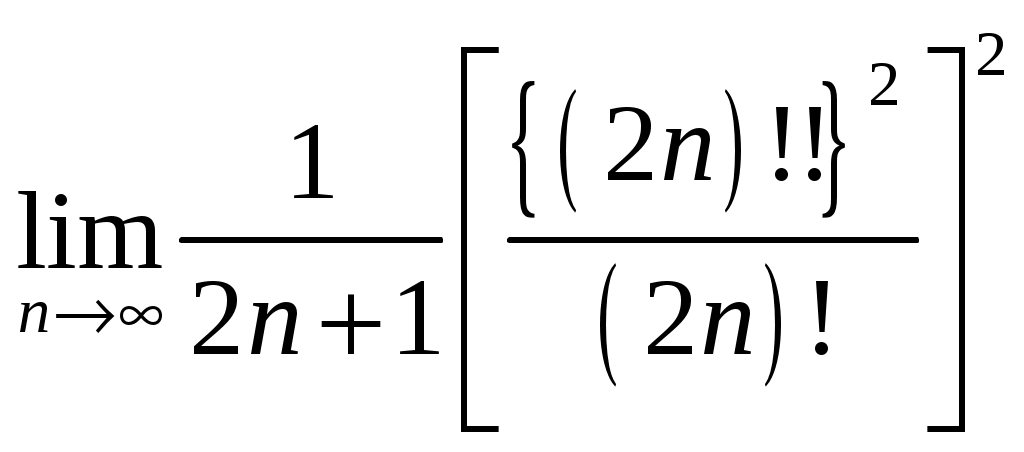 = = 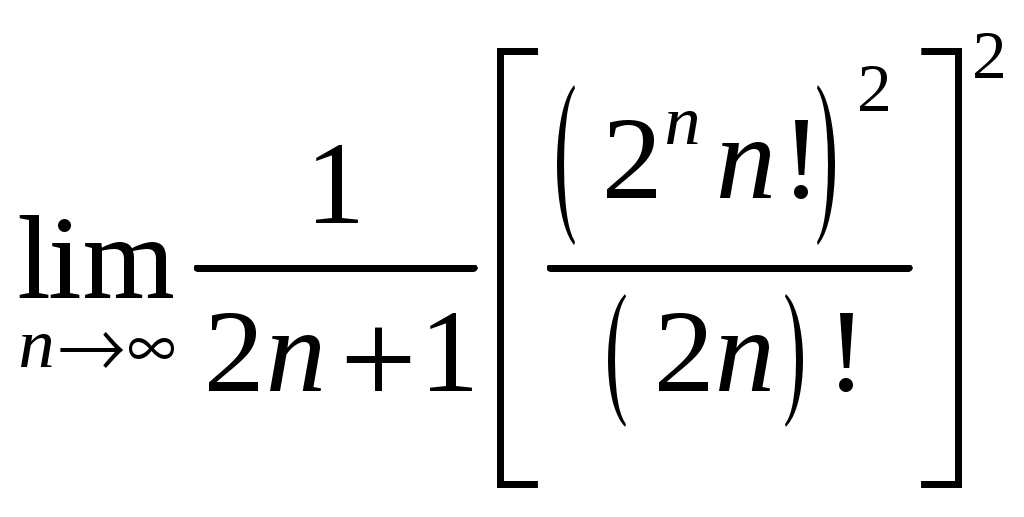 = …. = ….Подставляя вместо Тогда: РАЗДЕЛ 7. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ. §. Гамма – функция Г(z).Def: 1*. Прежде всего отметим что функция не определена при Для изучения сходимости Для него – Из сказанного ясно, что ряд, а вместе с ним и бесконечное произведение, сходятся абсолютно, при 2*. 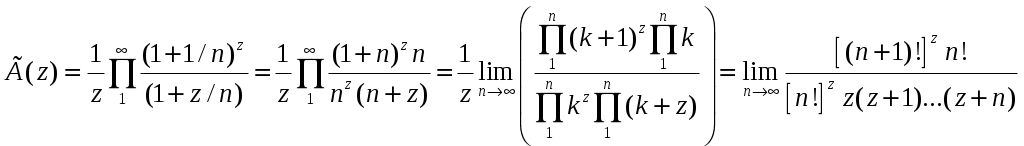 = == 3*. Формула понижения: 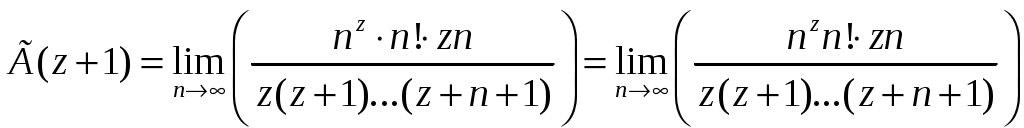 = == 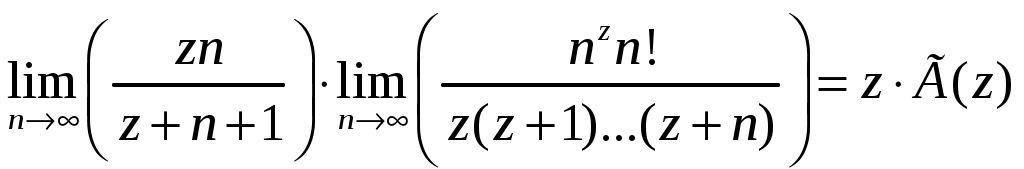 . .Тогда: 4*. Формула дополнения: 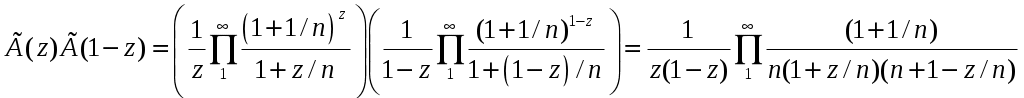 = == = 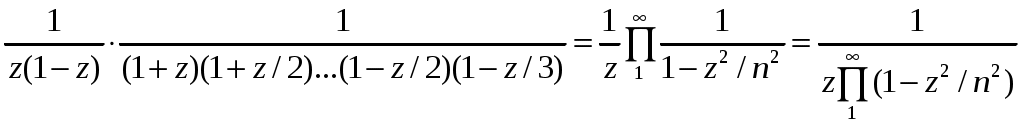 = …. = ….Полагая ….= 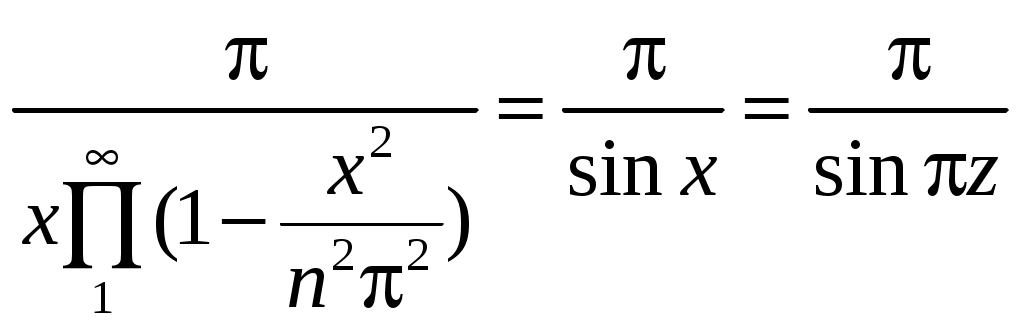 . .Из доказанной формулы дополнения • при • при 5*. Формула удвоения: 6*. Формула умножения: 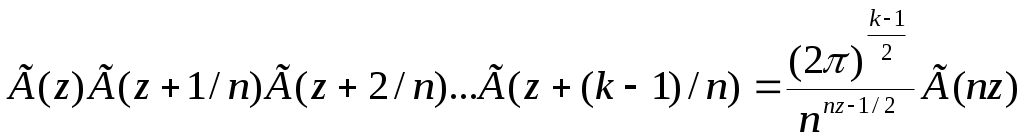 . .7*. Формула Лежандра (Эйлеров интеграл II - рода): 8*. Бета-функция (Эйлеров интеграл I – рода): §. СВЯЗЬ МЕЖДУ ЭЙЛЕРОВЫМИ ИНТЕГРАЛАМИ I-го И II-го РОДА 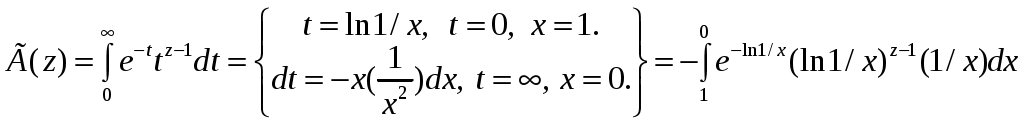 = == 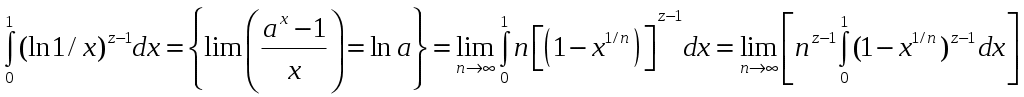 = == 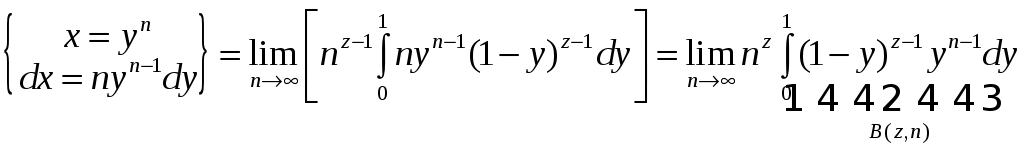 . .Функция В(z,n) – называется Бетта-функцией. §. БеТта – функциЯ В(а,b) 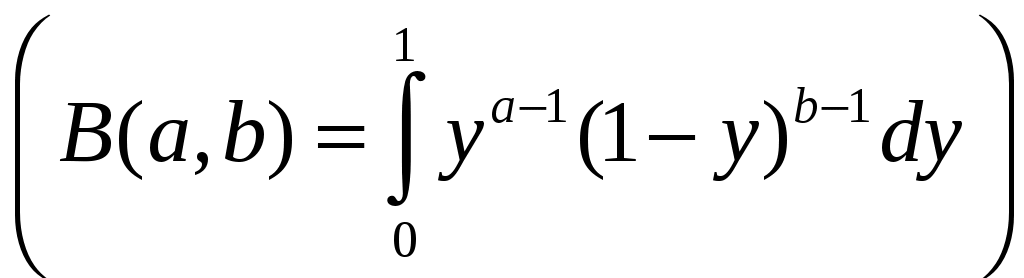 . .Изучим свойства введенной функции: а) Δ б). 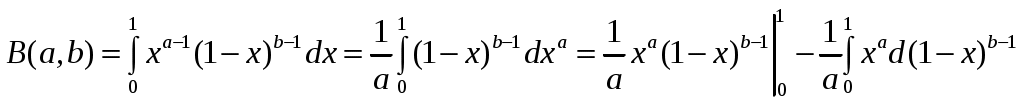 = == = = Итак, имеем: Если b – целое число, то: = Если, при этом, а – также целое, то: Эта формула полученная для целочисленных значениях аргументов справедлива и в общем случае: в). Еще одно выражение для Бета-функции: = Кстати, при b = 1 – a: §. ЕЩЕ РАЗ Гамма – функция Г(z).Возвращаемся к Гамма-функции. Нами установлено: Последняя выкладка показывает, что функция, введенная в п.7, как эйлеровый интеграл 2-го рода, действительно совпадает с Гамма-функцией, определенной в начале раздела. |
