Билет 1 Генеральная совокупность и выборка
 Скачать 69.88 Kb.
|
|
БИЛЕТ 1 Генеральная совокупность и выборка Определение. Генеральной совокупностью называют совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения. В практике статистических обследований различают два вида наблюдений: -сплошное, когда изучаются все объекты генеральной совокупности относительно некоторого признака; -не сплошное (или выборочное), когда изучается только часть объектов (выборочный метод) генеральной совокупности. Определение. Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов из генеральной совокупности. Объемомсовокупности (выборочной или генеральной) называют число объектов этой совокупности: N– объем генеральной совокупности. n– объем выборочной совокупности. Предполагается, что N>> n. Генеральная совокупность может быть как конечной, так и бесконечной. Суть выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности (выборке) выносить суждения о ее свойствах в целом. Для того, чтобы по выборке можно было достаточно уверенно судить об изучаемой случайной величине, выборка должна быть репрезентативной (или представительной). Репрезентативность выборки означает, что объекты выборки достаточно хорошо представляют генеральную совокупность. Рассмотрим на примере торта, он представляет собой генеральную совокупность, то есть весь комплекс, целое. Если мы отрежем кусок торта для исследований, то такая выборка является репрезентативной, потому что свойства этого куска точно такие же, как у всего остального торта и по нему можно определить, какими свойствами обладает все целое. Репрезентативность выборки обеспечивается выполнением трех требований: 1. Случайность отбора объектов выборки из генеральной совокупности, т. е. любой объект генеральной совокупности может быть отобран для исследования. 2. Независимость исследования каждого отдельного объекта выборки от результатов, полученных для других объектов. 3. Достаточный объем выборки. СЛАЙДЫ 3-7 БИЛЕТ 2 Статистические и вариационные ряды Любой исследуемый признак объектов генеральной совокупности, имеет некоторое статистическое распределение и может рассматриваться как случайная величина ξ. Тогда, значение исследуемого признака Y конкретного объекта выборки – это реализация случайной величины ξ, а результаты наблюдений, полученные для всех объектов выборки представляют собой множество расположенных в беспорядке реализаций случайной величины ξ: 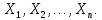 Определение. Ранжирование– это упорядочение полученных данных в порядке возрастания (или убывания). После проведения операции ранжирования получим: 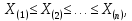 где элемент 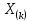 – называется k–ой порядковой статистикой.Если изучаемая случайная величина является дискретной, то после проведения операции ранжирования опытные данные нетрудно объединить в группы так, что в каждой отдельной группе возможные значения случайной величины будут одинаковыми. Определение. Различные возможные значения случайной величины ξ, соответствующие отдельной группе сгруппированного ряда наблюдаемых данных, называются вариантамии обозначаются 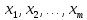 при этом  Для каждой группы сгруппированного ряда определяется ее численность, т.е. число, которое показывает, сколько раз встречается соответствующий вариант в ряде наблюдений. Определение. Численность отдельной группы сгруппированного ряда наблюдаемых данных называется частотойили весомсоответствующего ей варианта и обозначается  (i= 1,2,…,m), где i– номер варианта.Определение. Отношение частоты данного варианта к объему выборки называется частостью(относительной частотой, долей)этого варианта и обозначается 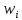 , т.е.:  Определение. Сгруппированным дискретным вариационным рядомназывается ранжированный в порядке возрастания (или убывания) ряд вариантов с соответствующими им частотами или частостями, который представляют в виде таблицы: 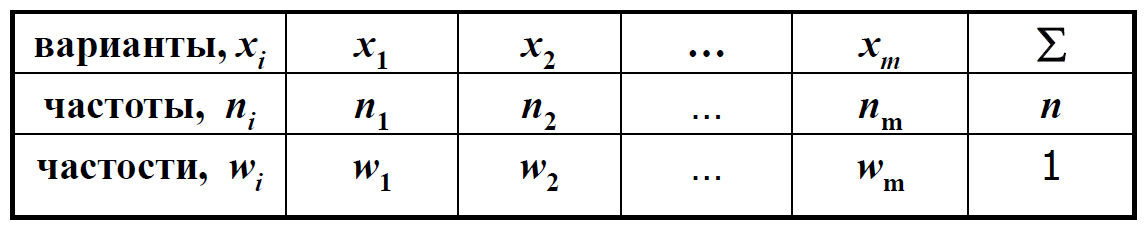 Пример 1. Изучается успеваемость студентов некоторого вуза по математике. По схеме собственно-случайной бесповторной выборки из 500 студентов вуза было отобрано 50. Результаты опроса студентов представляют собой следующий набор чисел: 3;4;5;4;2;3;3;3;5;4;3;5;5;2;3;5;3;5;3;5;4;4;3;3;4;3;3;3;4;3;4;3;5;3;4;4;3;5;3;3;5;4;2;5;3;4;2;3;5. n = 50 Построить дискретный вариационный ряд.  Если изучаемая случайная величина является непрерывной, строится интервальный вариационный ряд. Для этого также проводят группировку, разбивая весь интервал варьирования от xmin до xmax на отдельные интервалы, так чтобы каждое возможное значение принадлежало только одному из интервалов разбиения. Число возможных значений изучаемой случайной величины, принадлежащих i-му интервалу будем также обозначать (частота попадания в i-ый интервал). Число интервалов mследует брать не очень большим, чтобы после группировки ряд не был громоздким, и не очень малым, чтобы не потерять особенности распределения признака. Рекомендуемое число интервалов выбирается согласно формуле Стерджеса: 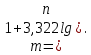 Длины интервалов можно брать как равными, так и различными. Будем предполагать, что длины интервалов одинаковые, величина которых (ширина интервала) определяется соотношением:  Границы интервалов рассчитываются по правилу:  до достижения 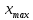 .СЛАЙДЫ 9-20 |