МНИ. МНИ 1-15. Билет 1 Статистическая обработка результатов эксперимента
 Скачать 152.44 Kb. Скачать 152.44 Kb.
|
|
Билет №1 1. Статистическая обработка результатов эксперимента Результат эксперимента, вне зависимости от его назначения, получается в виде набора чисел. Для того чтобы воспользоваться результатами проведенного опыта и делать на основании его какие-либо обобщения и выводы, требуется предварительно произвести статистическую обработку всех материалов эксперимента. Статистическая обработка эмпирических данных сводится в общем виде к следующему: Вычисление определенных характеристик объекта, Определение теоретических характеристик объекта по их экспериментальным значениям, Сравнение по определенным критериям экспериментальных значений характеристик с заданными теоретическими, Сравнение эмпирических и теоретических функций по определенным критериям согласия, Установление вида зависимости между случайными величинами. 2. Регистрация технологических процессов РТП представляет собой программно-аппаратный комплекс средств для осуществления мониторинга и контроля технологических параметров линий по производству кабелей. РТП является многоуровневой системой. С первого (нижнего) уровня сигналы датчиков (измерители диаметра, ИАСИ, термодатчики и др.) поступают на контроллер РТП, с которого они в цифровом виде передаются на РТП-сервер (верхний уровень) с установленным программным обеспечением (ПО). РТП-сервер осуществляет обработку полученных данных, их регистрацию, отображение и архивирование. РТП предоставляет следующие возможности: Сбор информации с датчиков и приборов, установленных на кабельной линии; ведение постоянного контроля работы приборов и механизмов, и регистрация данных через заданные промежутки времени; Отображение текущих показаний приборов в цифровом и графическом виде; архивация полученных данных; возможность просмотра архива измерений за любой промежуток времени или метража в табличном и графическом виде;  Билет №2 1. Построение эмпирических формул, корреляционный анализ, регрессия, интерполяция. Эмпирическая формула – это математическое уравнение, полученное опытным путём, методом проб и ошибок или как приближённая формула из экспериментальных данных. В общем виде задачу можно сформулировать следующим образом: пусть в результате исследования некоторой величины x значениям 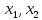 … , … , , поставлены в соответствие значения , поставлены в соответствие значения  … , … ,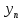 , некоторой величины y. Такая зависимость может быть изображена в виде функции , некоторой величины y. Такая зависимость может быть изображена в виде функции 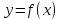 . .Корреляционный анализ – это метод, позволяющий обнаружить зависимость между несколькими случайными величинами. Построение коэффициентов корреляции основано на сумме произведений отклонений индивидуальных значений признаков 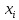 и и  от их средних значений от их средних значений  Регрессия – это односторонняя стохастическая зависимость, устанавливающая соответствие между случайными переменными Интерполяция – это способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. 2. Постановка эксперимента, поверка, калибровка, выбор измерительных приборов Постановка: 1. Разработать гипотезу, подлежащую проверке; 2. Создать программу экспериментальных работ; 3. Определить способы и приемы воздействия на объект исследования; 4. Создать условия для осуществления эксперимента; 5. Обеспечить эксперимент необходимым обслуживающим персоналом; 6. Разработать способ фиксирования хода и результатов эксперимента. Поверка служит подтверждением правильности измерений действующими СИ. Средства измерений до ввода в эксплуатацию, а также после ремонта подлежат первичной поверке, а в процессе эксплуатации — периодической поверке. Калибровка средств измерений (СИ) пришла на смену государственной поверке, которая являлась обязательной, а её результаты были действительны и актуальны в течение всего проверочного интервала. СИ необходимо калибровать, то есть измерять допустимую погрешность относительно эталона после изготовления оборудования, после его ремонта, при активной эксплуатации, после покупки бывшего в употреблении оборудования, аренды, импортировании. Результатом является либо калибровочный знак, наносимый непосредственно на СИ или запись в технических документах о размере выявленной погрешности. Выбор и назначение средств измерений должен удовлетворять требованиям получения действительных значений измеряемых величин с оптимальной точностью при наименьших затратах времени и материальных средств. Основными исходными данными для выбора средств измерений являются: Номинальное значение и разность между наибольшим и наименьшим предельными значениями измеряемой величины, указанные в нормативной, конструкторской или технологической документации; Условия выполнения измерений. Билет №3 1. Методы оптимизации. Выбор параметров оптимизации. Поиск минимальных и максимальных значений функции. Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом. Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции. Методы поиска: детерминированные, случайные (стохастические), комбинированные. Методы оптимизации По критерию размерности: методы одномерной оптимизации и методы многомерной опт-ции. По требованиям к гладкости и наличию у целевой функции частных производных: прямые методы, требующие только вычислений целевой функции в точках приближений; методы первого порядка: требуют вычисления первых частных производных функции; методы второго порядка: требуют вычисления вторых частных производных. Выбор параметров оптимизации (критериев оптимизации) является одним из главных этапов работы на стадии предварительного изучения объекта исследования, т.к. правильная постановка задачи зависит от правильности выбора параметра оптимизации, являющегося функцией цели. Под параметром оптимизации понимают характеристику цели, заданную количественно. Параметр оптимизации является реакцией (откликом) на воздействие факторов, которые определяют поведение выбранной системы. Нахождение макс/мин значений функций: 1. Найти производную функции, 2. Найти стационарные точки решив уравнение, 3. Вычислить значения функции в стационарных точках и на границах интервала, 4. Выбрать из полученных значений макс/мин и записать ответ 2. Требования и правила проведения НИР. Общие требования к научно-исследовательской работе: четкость и логическая последовательность изложения материала; убедительность аргументации; краткость и точность формулировок, исключающих возможность неоднозначного толкования; конкретность изложения результатов работы; обоснованность рекомендаций и предложений. Правилапроведения НИР: 1. НИР проводят в случае, когда разработку продукции невозможно или нецелесообразно осуществлять без проведения соответствующих исследований. Основание для проведения – заказ-наряд (договор); 2). НИР проводят с целью получения методами научного исследования: обоснованных исходных данных для разработки ТЗ; образцов новых веществ, материалов и т.п. Рекомендации законченных НИР должны обеспечивать возможность создания продукции высшей категории качества с учетом научного прогнозирования; 3. НИР проводят в соответствии с планами, разработанными и утвержденными в установленном порядке; 4. Организация (предприятие) проводящая НИР, несет ответственность за научно-технический уровень работы, за полноту и объективность представляемых результатов; 5. В зависимости от характера, сложности и объема работ в выполнении НИР могут принимать участие одна или несколько организаций; 6. Исполнитель НИР представляет в установленном порядке и в установленные сроки информационный материал о проведении НИР по формам и требованиям к их заполнению согласно установленному порядку. Билет №4 1. Спектральный анализ сигналов. Преобразование Фурье. При изучении сигналов и их преобразований линейными и нелинейными системами широко используются возможности спектрального анализа, который базируется на представлении сигналов рядом или интегралом Фурье. При этом определяется спектр сигнала, рассматриваемый как основная характеристика сигнала в частотной области. Знание этой характеристики позволяет определить область частот, занимаемую сигналом, применять принцип суперпозиции для анализа линейных систем. Преобразование Фурье – это операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами (подобно тому, как музыкальный аккорд может быть выражен в виде суммы музыкальных звуков, которые его составляют). Преобразование Фурье функции 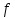 вещественной переменной является интегральным и задаётся следующей формулой: вещественной переменной является интегральным и задаётся следующей формулой: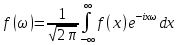 Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться. 2. Методы моделирования. Моделирование– способ научного познания, использующий замену изучаемого специальной моделью, которая воспроизводит главные особенности оригинала, и ее последующее исследование. Результат подобного исследования может быть распространен на оригинал с использованием специальных методов. Детерминированное моделирование отображает процессы, в которых предполагается отсутствие всяких случайных воздействий. Стохастическое моделирование отображает вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характеристики, т.е. набор однородных реализаций. Статическое моделирование служит для описания поведения объекта в какой-либо момент времени, а динамическое моделирование отражает поведение объекта во времени. Дискретное моделирование служит для описания процессов, которые предполагаются дискретными, соответственно непрерывное моделирование позволяет отразить непрерывные процессы в системах, а дискретно-непрерывные используется для случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов. Билет №5 1. Метод планирования эксперимента. Уравнение процесса. Параметр оптимизации, факторы процесса и их уровни. Метод планирования экспериментов разбивается на 4 основных этапа: I – Планирование, т.е подготовка проведения экспериментов; II – Проведение экспериментов; III – Обработка результатов, получение математической модели процесса; IV – Анализ математической модели, моделирование протекания процесса, его оптимизация. Определяют необходимое количество образцов и строят матрицу планирования. Количество необходимых образцов зависят от числа факторов и числа дублирования опыту Матрицы планирования заполняются в виде таблицы. Число строк в таблице соответствуют 2n+1, n – число факторов. Переменные параметры, изменяемые в процессе испытаний, называют факторами Для каждого фактора выбирают условный нулевой (исходный) уровень, диапазон и шаг варьирования переменных. Диапазон изменения факторов равен разности между верхним и нижним пределами данного фактора. В процессе установления варьирования решается вопрос о масштабе фактора, для выбора которого необходимо обратиться к теоретическим источникам, либо иметь некоторые априорные представления.  Параметр оптимизации – это признак, по которому мы хотим оптимизировать процесс. Он должен быть количественным, задаваться числом. Мы должны уметь его измерять при любой возможной комбинации выбранных уровней факторов. Множество значений, которые может принимать параметр оптимизации, будем называть областью его определения. Области определения могут быть непрерывными и дискретными, ограниченными и неограниченными. 2. Единицы физических величин. Система СИ. Система СИ была принята на XI Генеральной конференцией по мерам и весам, некоторые последующие конференции внесли в СИ ряд изменений. Система СИ определяет семь основных и производные единицы измерения, а также набор приставок. Установлены стандартные сокращённые обозначения для единиц измерения и правила записи производных единиц. В России действует ГОСТ 8.417-2002, предписывающий обязательное использование СИ. В нем перечислены единицы измерения, приведены их русские и международные названия и установлены правила их применения. По этим правилам в международных документах и на шкалах приборов допускается использовать только международные обозначения. Во внутренних документах и публикациях можно использовать либо международные, либо русские обозначения (но не те и другие одновременно). Основные единицы: килограмм, метр, секунда, ампер, кельвин, моль и кандела. В рамках СИ считается, что эти единицы имеют независимую размерность, т. е. ни одна из основных единиц не может быть получена из других. Производные единицы получаются из основных с помощью алгебраических действий, таких как умножение и деление. Некоторым из производных единиц в Системе СИ присвоены собственные названия. Приставки можно использовать перед названиями единиц измерения; они означают, что единицу измерения нужно умножить или разделить на определенное целое число, степень числа 10. Например приставка «кило» означает умножение на 1000 (километр = 1000 метров). Приставки СИ называют также десятичными приставками. Билет №6 1. Методы оценки адекватности математических моделей Оценка адекватности проводится с помощью специально разработанных критериев. Критерий Фишера – для проверки математической модели на адекватность вычисляется опытное значение критерия Фишера. Опытное значение сравнивается с теоретическим значением взятом при заданном уровне значимости  . . Опытное значение критерия Фишера берется равным отношению дисперсии адекватности к общей дисперсии опытов.  Где:  – дисперсия адекватности, – дисперсия адекватности, 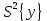 – дисперсия опытов – дисперсия опытов – модель адекватно описывает реальный процесс, – модель адекватно описывает реальный процесс,  – уравнение неадекватно описывает эксперементальные данные – уравнение неадекватно описывает эксперементальные данныеКритерий Кохрена – используется если колличество дисперсий больше двух и одна значительно больше остальных  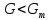 – дисперсия считается однородной, в противном случае неоднородной – дисперсия считается однородной, в противном случае неоднородной 2. Косвенные и прямые измерения физических величин. Погрешности измерения физических величин. Прямые измерения– это измерения, при которых искомое значение величины y находят непосредственно из опытных данных х. Математическая зависимость между измеряемыми и определяемыми путем прямых измерений величинами называется уравнением измерения. Оно имеет вид y = x. Косвенные измерения– это измерения, при которых искомое значение величины находят на основании известной математической зависимости между этой величиной и величинами-аргументами, полученными при прямых измерениях. Уравнение косвенного измерения имеет вид: 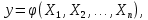 Где Где 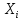 аргументы. аргументы.Абсолютная погрешность измерения – алгебраическая разность между измеренным x и истинным  значениями измеряемой величины: значениями измеряемой величины: 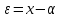 Относительная погрешность– отношение абсолютной погрешности к истинному значению измеряемой величины, которая измеряется в долях измеряемой величины либо в процентах: 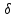 = =  / /  Случайная погрешность – это составляющая погрешности, изменяющаяся случайным образом при повторных измерениях одной и той же величины, то есть погрешность, величина и знак которой не могут быть точно предсказаны. Случайную погрешность невозможно устранить, однако величину случайной погрешности можно оценить и найти способ её уменьшения. Систематическая погрешность – это составляющая погрешности, остающаяся постоянной или закономерным образом изменяющаяся при повторных измерениях одной и той же величины. Причинами систематической погрешности являются, главным образом, несовершенство метода, средства или объекта измерения. Промахами – это погрешности измерений, превышающие по своему значению систематические или случайные погрешности. Основными причинами грубой погрешности являются неправильное или небрежное считывание показаний, дефекты средств измерений, незнание или пренебрежение источниками погрешности, случайное, сильное внешнее воздействие (помеха). Билет №7 1. Приборы и средства измерения. Класс точности приборов. Измерительный прибор – это средство измерения, при использовании которого получают значения физической величины, принадлежащие фиксированному диапазону. Измерительные приборы прямого действия – это приборы, посредством которых можно получить значение измеряемой величины непосредственно на устройстве. Измерительный прибор сравнения – это прибор, посредством которого значение измеряемой величины получается при помощи сравнения с известной соответствующей величиной. Средство измерения (СИ) – это техническое средство или совокупность средств, применяющееся для осуществления измерений и обладающее нормированными метрологическими характеристиками. При помощи средств измерения физическая величина может быть не только обнаружена, но и измерена. Класс точности — обобщённая характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений. Для стрелочных приборов принято указывать класс точности, который записывается в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. 2. Сущность метода конечных разностей при математическом моделировании Суть метода конечных разностей заключается в следующем. Интервал  разбивается точками разбивается точками  на на  равных отрезков длиной равных отрезков длиной  (рис. 1), причем (рис. 1), причем   , ,  . Это множество точек называется сеткой с узлами . Это множество точек называется сеткой с узлами  и шагом и шагом  . . Рис. 1. Конечно, разностная сетка К достоинствам метода конечных разностей следует отнести его высокую универсальность. Применение этого метода характеризуется относительной простотой построения решающего алгоритма и его программной реализации. При практическом применении метода конечных разностей важно иметь возможность уменьшения различия между приближенным (сеточным) решением и точным решением исходной задачи до уровня допустимой погрешности. Такая возможность в первую очередь связывается со свойством сходимости разностной схемы. Билет №8 1. Вероятностные методы обработки данных Вероятностный метод – это метод доказательства существования математического объекта с заданными свойствами. В основном используется в теории чисел, линейной алгебре и математическом анализе. Основа статистики и статической обработки результатов является нормальное распределение Гаусса (в результате большого количества измерений возможно получить значение полученной величины, соответствующей его истинному значению).  Существует такое понятие как плотность вероятности. То закон Гаусса представляется в виде такой кривой : Существует такое понятие как плотность вероятности. То закон Гаусса представляется в виде такой кривой :Р(х)=  G=  В технике принято, что для общетехнических систем вероятность 95% является достаточной. Для ответственных систем принимают вероятность 98%. Теория вероятности достаточно широко применяется при научных исследованиях, в том числе и в сварочном производстве. Если некоторые события А появляются, как следствием m событий из общего числа событий n, то вероятность события А составляет  Метод Монте-Карло  Этот метод основан на генерации случайных чисел и является составной частью теории вероятности. Случайное число – это такое число, определять значение которого заранее практически невозможно. Генерация случайных чисел используется для решения практических задач. Определение числа Пи Этот метод основан на генерации случайных чисел и является составной частью теории вероятности. Случайное число – это такое число, определять значение которого заранее практически невозможно. Генерация случайных чисел используется для решения практических задач. Определение числа ПиВ пределах прямоугольника генерируются случайные числа общим количеством N.   Затем считается количество точек, которые находятся внутри сектора. Общее число внутри сектора равно Затем считается количество точек, которые находятся внутри сектора. Общее число внутри сектора равно  2. Общие требования к тестовым документам Работа оформляется в соответствии с ГОСТ 2.105 – 95 «Общие требования к текстовым документам». Текст набирается с соблюдением следующих правил: Работа выполняется на белой бумаге формата А4 (210 х 297 мм). Текст работы излагается на одной стороне листа; Текст должен быть набран через полтора интервала, шрифт «Times New Roman», размер шрифта № 12. Параметры страницы: левое поле – 3,0 см, правое поле – 1,0 см, верхнее поле –1,5 см, нижнее поле – 2,0 см.; Текст должен быть расположен по ширине страницы с учетом полей. Слова внутри абзаца разделяются только одним пробелом; Набор текста осуществляется без переносов; Кавычки («»), скобки ([],()), маркеры и другие знаки должны быть сохранены аналогичными на протяжении всего материала; Билет №9 1. Понятие о математической модели процесса Математическая модель– это система математических соотношений, описывающих изучаемый процесс или явление. При планировании эксперимента под математической моделью часто понимают уравнение, связывающее параметр оптимизации с факторами. Такое уравнение называют также функцией отклика. В общем виде функция отклика может быть представлена выражением:  Где:  , ,  , …, , …,  – независимые переменные факторы. – независимые переменные факторы.Уравнение регрессии, полученное по результатам опытов, имеет вид  Где  , ,  , ,  , ,  , ,  – коэффициенты регрессии. – коэффициенты регрессии.2. Организационное и методическое обеспечение проведения экспериментов и обработки результатов Правильно составленная и выбранная методика гарантирует надежность полученных данных при выполнении исследований. Методика должна включать и теоретические, и экспериментальные исследования. Теоретические исследования проводят методом моделирования. Используемая модель представляет собой искусственную систему, которая отображает интересующие исследователя свойства изучаемого объекта оригинала. Полученная модель должна отображать существенные явления процесса и при этом быть оптимальной. Этапы в процессе моделирования на ПК: 1. Выбор характеристик и основных факторов процесса и установление взаимосвязи между ними с использованием математического аппарата. 2. Подбор или составление программного обеспечения. 3. Проведение исследований на персональных компьютерах. 4. Анализ полученных результатов. 5. Сопоставление этих результатов с опытными данными. Экспериментальные исследования − основной метод получения новых научных знаний, основанный либо на эксперименте, либо на наблюдении явления в точно учитываемых условиях. В ходе эксперимента следят за ходом процесса, управляя им и стремясь воссоздать его каждый раз при повторении заданных условий. Цель эксперимента проверка теоретических положений, а также получение количественных данных для оценки значимости факторов разрабатываемой модели. План или программа любого эксперимента содержит: 1. Наименование темы проводимого исследования; 2. Формулировка рабочей гипотезы; 3. Формулировку и описание методики эксперимента; 4. Перечень используемых установок, приборов и материалов; 5. Перечень исполнителей с конкретными заданиями; 6. Календарный план работ с разбивкой по срокам; 7. Смета работ. Важную роль, определяющую эффективность эксперимента, играет выбор варьируемых факторов (характеристик), влияющих на исследуемый процесс. В ряде случаев необходим предварительный поисковый эксперимент, проводимый для правильного отбора параметров. В случае большого числа переменных целесообразно использовать принцип многофакторного анализа. Билет №10 1. Программное обеспечение математических методов обработки (опции Excel) Появление электронных таблиц (табличных процессоров) привело к тому, что статистические методы, ранее доступные лишь узкому кругу математиков, стали использоваться широким кругом специалистов разных областей. Дальнейшее развитие программного обеспечения привело к созданию большого количества прикладных пакетов по статистике. Удобной универсальной вычислительной средой для решения задач ОЭД является табличный процессор MS Excel. В MS Excel возможно: оценить параметры и определить законы распределения, вычислить коэффициенты уравнения линейной регрессии, вычислить коэффициенты корреляции, провести проверку значимости уравнения линейной регрессии по Критерию Фишера, построить нелинейную регрессию с добавлением линии тренда, изучить взвешенный метод наименьших квадратов и тд. 2. Метрологическое обеспечении экспериментальных исследований Измерение – это нахождение значения физической величины опытным путем с помощью специальных технических средств (ГОСТ 16263-70). Метрология занимается теорией и практикой измерения. Это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. К основам метрологии относятся: единицы физических величин, системы единиц (СИ); методы и средства измерений; методы определения точности измерений; основы обеспечения единства измерений. Основные методы измерения Метод непосредственной оценки – определяет значение величины по отсчетному устройству измерительного прибора прямого действия (например, измерение массы на циферблатных весах). Нулевой метод – применяется для результирующего эффекта воздействия величины на прибор до нуля (например, измерение массы на рычажных весах с уравновешением гирями). Дифференциальный метод – на измерительный прибор воздействует разность измеряемой и известной величины, воспроизводимой мерой (например, измерения, выполняемые при проверке мер длины сравнением с образцовой мерой на компараторах). Средства измерений (измерительные приборы, меры, установки и системы) являются обязательной и неотъемлемой частью экспериментальных исследований. Они являются совокупностью технических средств, имеющих нормированные погрешности, которые дают необходимую информацию для экспериментатора. Все средства измерения, используемые в научных исследованиях, проходят обязательную периодическую поверку на точность (каждые 1-2 года). Поверка предусматривает уменьшение погрешностей прибора. Важнейшим фактором успешного проведения научных исследований является метрологическое обеспечение научных исследований и особенно обеспечение единства измерений, однообразие средств измерения. Поэтому без успешного развития метрологии невозможен прогресс в развитии науки и, наоборот, без успешного развития науки невозможен прогресс в метрологии. Билет №11 1. Регистрация, документирование технологических процессов сварки на примере регистратора МРС. Назначение и область применения Регистраторы технологических процессов «МРС-02м» предназначены для измерения и регистрации амплитудного значения напряжения в технологических процессах сварочного производства, других технологических процессах в различных отраслях промышленности, а также измерения и регистрации напряжения постоянного тока в цифровом коде. Поверка Поверка регистраторов технологических процессов «МРС-02м» осуществляется в соответствии с методикой поверки, согласованной ГЦИ СИ ФГУ «Нижегородский ЦСМ». Встроенная в устройство программа позволяет получать графическое отображение принятых сигналов и результатов их обработки на индикаторе устройства. Регистратор обеспечивает передачу принятых данных по стандартному каналу RS-232 в персональный компьютер типа для дальнейшей обработки. Межповерочный интервал 2 года. Перечень оборудования необходимого, для поверки: Прибор для поверки вольтметров В1-9. Калибратор программируемый П32(). Частотомер электронно-счетный 43-54. Нормативные и технические документы ГОСТ 12997-84 «Изделия Г'СП. Общие технические условия». Техническая документация на регистраторы технологических процессов «МРС-02м» ООО «ТЭЛМА». Тип регистраторы технологических процессов «МРС-02м» с заводскими номерами 01_10.04 - 14_10.04 утвержден с техническими и метрологическими характеристиками. 2. Встроенные в Excel средства обработки экспериментальных данных. Microsoft Excel — программа для работы с электронными таблицами, созданная корпорацией Microsoft. Она предоставляет возможности экономико-статистических расчетов, графические инструменты и язык макропрограммирования VBA В настоящее время Excel – ведущая программа обработки электронных таблиц, представляющая собой достаточно мощное средство разработки информационных систем, которое включает как электронные таблицы, так и средства визуального программирования. Электронные таблицы позволяют: Решать различные вычислительные задачи (численные решения дифференциальных, интегральных, матричных систем уравнений, решение задач линейного программирования и многое другое); Решать задачи моделирования (на основе аппарата решения задач линейного программирования, выбирать оптимальный вариант в массе экономических задач и задач планирования, многократно рассчитывать по формулам различные величины и строить зависимости их значений от параметров); Осуществлять задачи обработки данных: статистического анализа; построения диаграмм, ведение баз данных. Билет №12 1. Цель, задачи и методы проведения эксперимента. Эксперимент – метод исследования системы управления в определенных условиях ее функционирования, которые могут быть реальными или искусственно созданными исследователем, для получения необходимой информации. Целью всякого эксперимента является проверка гипотез о причинной связи между явлениями: исследователь создает определенную ситуацию, приводит в действие гипотетическую причину и наблюдает за изменениями событий, фиксирует их соответствие или несоответствие предположениям, гипотезам. Задачи Проверка результатов теоретических исследований. Выбор и уточнение констант теоретических моделей. Планирование эксперимента с целью математического описания объекта. (получение математической модели) Планирование эксперимента при поиске оптимальных условий. (отыскание значений варьируемых факторов, т. е. max или min значение). Методы Методы эмпирического уровня: наблюдение и измерение Методы теоретического уровня: формализация, идеализация, гипотеза, теория и закон Методы комплексного исследования: синтез, анализ, обобщение, индукция, абстракция, дедукция, интуиция, доказательство, аналогия и моделирование 2. Методы оценки экономической эффективности исследований. Под экономической эффективностью научных исследований в целом понимают снижение затрат общественного и живого труда на производство продукции в той отрасли, где внедряют законченные НИР и ОКР. Для оценки эффективности исследований применяют разные критерии, характеризующие степень их результативности. Фундаментальные исследования начинают возвращать капиталовложения лишь спустя значительный период после начала разработки. Фундаментальные теоретические исследования трудно оценить количественными критериями эффективности. Обычно можно установить только качественные критерии. Оценка эффективности исследований. Об эффективности любого исследования можно говорить только по его окончании. Где  – предполагаемый экономический эффект от внедрения; – предполагаемый экономический эффект от внедрения;  – затраты на научные исследования. – затраты на научные исследования.К Где  – стоимость продукции за год после освоения научного исследования и внедрения в производство; – стоимость продукции за год после освоения научного исследования и внедрения в производство;  – продолжительность производственного внедрения в годах; – продолжительность производственного внедрения в годах;  – общие затраты на выполнение научного исследования, опытное и промышленное освоение продукции и годовые затраты на ее изготовление по новой технологии. – общие затраты на выполнение научного исследования, опытное и промышленное освоение продукции и годовые затраты на ее изготовление по новой технологии.Билет №13 1. Особенности моделирования технологических процессов (на примере СП, ОД и ПК). Моделирование– способ научного познания, использующий замену изучаемого специальной моделью, которая воспроизводит главные особенности оригинала, и ее последующее исследование. Моделирование сварочных процессов производится с целью оценки характера протекания процессов, изучение особенностей, а также с целью непрерывного мониторинга процесса в соответствие с полученной математической моделью. Методология научных исследований в сварочном производстве. 1 группа – оценка геометрической формы и размеров сварочных швов, а также формы и размеры разделки сварочных деталей перед сваркой. 2 группа – измерение прочностных характеристик сварочных образцов. Наиболее распространенными являются: определение временного сопротивления на разрыв на разрывной машине. 3 группа – относят вопросы параметров процесса. Для дуговых способов основными параметрами являются: сварочный ток и напряжение, скорость сварки и скорость подачи проволоки. Определяющим параметром режима является сварочный ток. Моделирование процессов ОМД имеет высокое научное и прикладное значение, т.к. построение рабочей модели способствует более качественной оценки и планированию результатов научной деятельности для внедрения новых прогрессивных технологий. В последние годы способами ОМД получают высококачественные изделия с высокими рабочими параметрами. Моделирование на ПК – один из самых мощных инструментов познания, анализа и проектирования. Сущность методологии моделирования на ПК состоит в замене исходного технологического объекта его «образом» - математической моделью – и в дальнейшем изучении модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов. 2. Основные принципы организации и управления научным коллективом. Принцип информированности о существе проблемы. Любое полезное нововведение может быть воспринято позитивно и даже с энтузиазмом, если членам коллектива станет ясно, какие задачи будут решены в результате их работы. Принцип превентивной оценки работы заключается в соответствующем информировании сотрудников для исключения отождествления ими временных затруднений с отрицательными последствиями управленческого мероприятия. Принцип инициативы снизу. Работа выполняется значительно быстрее в том случае, если информация о предстоящей работе войдёт в сознание непосредственных исполнителей как дело полезное и нужное, как самим работникам, так и обществу. Принцип тотальности. Работники всех звеньев, на которых прямо или косвенно окажет влияние новое задание, должны быть не только заранее проинформированы о возможных проблемах, но и привлечены к участию в их решении. Принцип непрерывности деятельности. Завершение одной разработки должно совпадать с началом разработки следующего задания. Принцип перманентного информирования. Руководитель научного коллектива должен систематически информировать всех сотрудников коллектива как о достигнутых успехах в решении задачи, так и о трудностях, проблемах, срывах. Принцип индивидуальной компенсации. Руководство должно учитывать особенности ценностных ориентаций людей, их потребностей и интересов. Билет №14 1. Виды обеспечения проведения научных исследований и обработки результатов НИР. Научные исследования можно разделить на: Фундаментальные–расширение теоретических знаний. Получение новых научных данных о процессах, явлениях, закономерностях, существующих в исследуемой области; научные основы, методы и принципы исследований. Поисковые–увеличение объема знаний для более глубокого понимания изучаемого предмета. Разработка прогнозов развития науки и техники; открытие путей применения новых явлений и закономерностей. Прикладные–разрешение конкретных научных проблем для создания новых изделий. Получение рекомендаций, инструкций, расчетно-технических материалов, методик и т.д. Фундаментальные и поисковые НИР обычно не входят в комплекс работ по созданию и освоению новых товаров. Непосредственно к процессам создания новых товаров относятся прикладные НИР. Оценка научной результативности НИР производится с помощью системы взвешенных балльных оценок. Для фундаментальных НИР рассчитывается только коэффициент научной результативности, а для поисковых работ нужен еще и коэффициент научно-технической результативности. Коэффициент научно-технической результативности определяется по формуле:  где  – число оцениваемых параметров; – число оцениваемых параметров;  – коэффициент влияния параметра на научно-техническую результативность; – коэффициент влияния параметра на научно-техническую результативность;  – коэффициент относительного повышения параметра по сравнению с базовым значением. – коэффициент относительного повышения параметра по сравнению с базовым значением.2. Оценка адекватности математических моделей. Математическая модель– это система математических соотношений, описывающих изучаемый процесс или явление. При планировании эксперимента под математической моделью часто понимают уравнение, связывающее параметр оптимизации с факторами. Оценка адекватности проводится с помощью специально разработанных критериев. Критерий Фишера – для проверки математической модели на адекватность вычисляется опытное значение критерия Фишера. Опытное значение сравнивается с теоретическим значением взятом при заданном уровне значимости  . . Опытное значение критерия Фишера берется равным отношению дисперсии адекватности к общей дисперсии опытов.  Где:  – дисперсия адекватности, – дисперсия адекватности,  – дисперсия опытов – дисперсия опытов – модель адекватно описывает реальный процесс, – модель адекватно описывает реальный процесс,  – уравнение неадекватно описывает эксперементальные данные – уравнение неадекватно описывает эксперементальные данныеКритерий Кохрена – используется если колличество дисперсий больше двух и одна значительно больше остальных   – дисперсия считается однородной, в противном случае неоднородной – дисперсия считается однородной, в противном случае неоднородной Билет №15 1. Понятие, методы математического моделирования. Математическая модель– это система математических соотношений, описывающих изучаемый процесс или явление. При планировании эксперимента под математической моделью часто понимают уравнение, связывающее параметр оптимизации с факторами. Моделирование – это исследование, какого-либо объекта или системы объектов путем построения и изучения их моделей. Это использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов. Методы математического моделирования Аналитические методы моделирования. Аналитические методы позволяют получить характеристики системы как некоторые функции параметров ее функционирования. Численные методы моделирования. Математическая модель представляет собой систему линейных, нелинейных уравнений, но решается система уравнений методами вычислительной математики. Имитационные методы моделирования. Для анализа систем, преобладающими в которых являются стохастические воздействия. Суть имитационного моделирования заключается в имитации процесса функционирования системы во времени, с соблюдением таких же соотношений длительности операций как в системе оригинале. Вероятностно-статистические методы моделирования. Применяются для описания зависимостей между выходными характеристиками системы и входными переменными (параметрами) системы. 2. Постановка эксперимента. Постановка эксперимента – это комплекс методов математической статистики, направленных на постановку опытов и проведение рациональных измерений, подверженных случайным ошибкам. Основная цель постановки эксперимента – достижение максимальной точности измерений при минимальном количестве произведенных опытов и сохранении статистической достоверности результатов. Этапы постановки эксперимента Установление цели эксперимента – постановка целей и задач проведения эксперимента; Уточнение условий проведения эксперимента – выбор оборудования, сроков работ, способа проведения эксперимента и т.п.; Выбор входных и выходных параметров – выбор зависимой измеряемой переменной, определение случайных и детерминированных независимых переменных; Установление необходимой точности результатов измерений – выбор компромисса между минимальным числом испытаний и статистической достоверностью получаемых результатов; Составление плана и проведение эксперимента – количество и порядок испытаний, задание совокупности значений задаваемых переменных-факторов и их взаимодействий в эксперименте; Статистическая обработка результатов эксперимента – применение методов математической статистики для обработки результатов, построение математической модели эксперимента; Формулирование выводов. |
