билеты. Билет + ответы по геом. Билет 1 Виды треугольников по длине сторон. Периметр треугольника
 Скачать 488.58 Kb. Скачать 488.58 Kb.
|
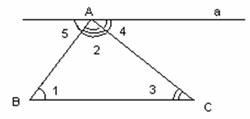
1 2 Билет №1 1. Виды треугольников по длине сторон. Периметр треугольника. Треугольники бывают: Равнобедренный (равны две стороны), разносторонний (все стороны по величине разные), равносторонний -все стороны равны Периметром треуг называется сумма длин его сторон) 2. Смежные углы (определение). Теорема о сумме смежных углов. Смежными называются два угла, у которых одна сторона общая, а две другие являются дополнительными лучами (т.е. имеют общее начало и дополняют друг друга до прямой). Сумма смежных углов равна 180°. Дано: ∠АОВ и ∠ВОС смежные. Доказать: ∠АОВ + ∠ВОС = 180° Доказательство: ∠АОС = ∠АОВ + ∠ВОС по свойству измерения углов, ∠АОС = 180°, так как является развернутым, ⇒ ∠АОВ + ∠ВОС = 180° 3. Задача по теме "Признаки равенства треугольников". Отрезки AC и BD пересекаются в точке О. AO=OC, BO=OD. При проведении отрезков AB и CD образуются треугольники BAO и OCD. Докажите, что ∆ BAO=∆ OCD. Билет №2 1. Отрезок (определение). Середина отрезка. Основное свойство расположение точек на прямой. Отрезок - это часть прямой, которая ограничена двумя точками, т.е. она имеет начало и конец, а значит можно измерить её длину. Середина отрезка - это точка на заданном отрезке, находящаяся на равном расстоянии от обоих его концов отрезка. из трёх точек на прямой одна и только одна лежит между двумя другими. 2. Свойства равнобедренного треугольника (доказательство одного из них). Свойства равнобедренного треугольника: 1. В равнобедренном треугольнике углы при основании равны. Доказательство: пусть АВС - равнобедренный треуг с основанием АВ. Докажем, что у него А= В. Тр САВ равен тр СВА по первому признаку равенства треугДействительно, СА=СВ, СВ=СА, угол С= углу С.Из равенства треугольников следует, что угол А= углу В. Теорема доказана. 2 В равнобедренном треуг биссектриса , проведённая к основанию , является медианной и высотой . Доказательство: Рассмотрим треугольники ACF и BCF (важно правильно их назвать!) 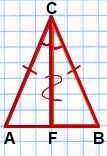 1) AC=BC (по условию (как боковые стороны равнобедренного треугольника)) 2) ∠ACF=∠BCF (так как CF — биссектриса по условию). 3) сторона CF — общая. Значит, ∆ ACF=∆ BCF (по двум сторонам и углу между ними). Из равенства треугольников следует равенство соответствующих сторон и углов. Таким образом, AF=BF, следовательно, CF — медиана. ∠AFC=∠BFC. А так как эти углы — смежные, значит, они прямые: ∠AFC=∠BFC=90º. Значит, CF — высота. Что и требовалось доказать. 3. Задача по теме "Окружность и ее элементы". Найдите длину радиуса окружности, если длина диаметра равна 14,5 см. Билет № 3 1. Основные геометрические фигуры на плоскости. Основное свойство принадлежности точек и прямых. Основными геометрическими фигурами на плоскости являются точка и прямая. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну. 2. Построение треугольника по трём сторонам. Даны три отрезка: a,b иc, равные сторонам искомого треугольника.. В этом случае перед началом построения необходимо убедиться, исполняется ли неравенство треугольника (длина каждого отрезка меньше суммы длин двух остальных отрезков), и эти отрезки могут быть сторонами треугольника. Если да, то:, 1. Провести прямую. 2. На прямой от выбранной точки A отложить отрезок, равный данному отрезку a, и отметить другой конец отрезка B. 3. Провести окружность с центром A и радиусом, равным отрезку b. 4. Провести окружность с центром B и радиусом, равным отрезку c. 5. Точка пересечения окружностей является третьей вершиной искомого треугольника. 3. Задача по теме "Вертикальные углы". Один из вертикальных углов равен 45º. Найдите остальные углы. Билет № 4 Высота, биссектриса, медиана треугольника (определения). Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса - это отрезок, делящий угол треугольника на две равные части. Высота треугольника - это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение. Теорема о свойстве катета, лежащего против угла в 30º. Так как сумма острых углов прямоугольного треугольника равна 90º, то∠B=90º-∠A=90º-30º=60º.Построим треугольник ADC, равный треугольнику ABC.В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º ( по построению).Отсюда, ∠BAD=∠CAD+∠CAB=60º.Следовательно, в треугольнике ABD все углы равны:∠BAD=∠D=∠B=60º.Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.BC=DC (по построению), поэтому Задача по теме " Признаки параллельности прямых". Один из внутренних накрест лежащих углов, образованных при пересечении двух параллельных прямых третьей прямой, равен 50º. Найдите градусные меры остальных углов. Билет № 5 Взаимное расположение двух прямых. Основное свойство параллельных прямых. 1)прямые пересекаются (т. е. имеют одну общую точку), 2) прямые параллельны и не совпадают, 3) прямые совпадают( множ-во общих точек) Через точку не лежащую на прямой, можно провести прямую параллельную данной, причем только одну. Вертикальные углы (определение). Свойства вертикальных углов. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны Дано: – 1 и – 2 – вертикальные углы. Доказать: – 1 = – 2. Доказательство. – 3 является смежным и с – 1, и с – 2. Сумма смежных углов равна 180°, поэтому – 1 + – 3 = 180о , – 2 + – 3 = 180о . Отсюда получаем, что – 1 = 180о –– 3, – 2 = 180о – – 3. Пра- вые части равенств равны, значит, равны и левые. Следовательно, – 1 = – 2. Итак, вертикальные углы равны 3. Задача по теме " Соотношения между сторонами и углами треугольника". В треугольнике ABC AB=4 см, AC=6 см,BC=5 см. Какой угол треугольника наименьший, а какой наибольший? Билет №6 Полуплоскость. Луч (определение). Основное свойство расположения точек относительно прямой на плоскости. Любая прямая на плоскости разделяет её на две части, которые называются полуплоскостями. Полуплоскость – это часть плоскости, лежащая по одну сторону от любой прямой на этой плоскости. Луч — это часть прямой, состоящая из всех точек этой прямой, лежащих по одну сторону от одной её точки. Эта точка называется началом луча. Первый признак равенства треугольников. Доказать, что треугольник ABC равен треугольнику DEF. Доказательство: Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F. При этом отрезки СА и СВ наложатся на отрезки FE и FD. А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED. Это в свою очередь даст совмещение вершин А и D, В и Е. Следовательно, треугольники полностью совместятся, а значит, они равны. Теорема доказана. 3. Задача по теме " Сумма углов треугольника". В треугольнике ABC даны два угла:  =32º, =32º, 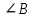 =57º. Найдите третий угол. =57º. Найдите третий угол.Билет № 7 Угол (определение). Измерение углов. Основные свойства измерения углов. У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла). За единицу измерения углов обычно принимается угол, составляющий одну сто восьмидесятую часть развернутого угла. Считают, что величина этого угла равна одному градусу, обозначают 1о. Градусная величина угла показывает, сколько раз угол в один градус и его части укладываются в этом угле. Прибор для измерения транспортир. 1)Каждый угол имеет определенную градусную меру большую нуля. 2)Развернутый угол равен 180 градусам. 3) Градусная мера угла равна сумме градусных мер углов,на которые он разбивается любым лучом,проходящим между его сторонами. Второй признак равенства треугольника. (Второй признак равенства треугольников — по стороне и двум прилежащим к ней углам) Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны. Дано:ΔABC, ΔA1B1C1, AB=A1B1, ∠A=∠A1, ∠B=∠B1. Доказать: ΔABC= ΔA1B1C1 Доказательство: Так как AB=A1B1, то треугольник A1B1C1 можно наложить на треугольник ABC так, чтобы сторона A1B1 совместилась со стороной AB, точки C1 и С лежали по одну сторону от прямой AB. Поскольку ∠A=∠A1, сторона A1С1 при этом наложится на луч AC. Так как ∠B=∠B1, сторона B1C1 наложится на сторону BC. Точка С1 принадлежит как стороне A1С1, так и стороне B1C1, поэтому С1лежит и на луче AC, и на луче CB. Лучи AC и CB пересекаются в точке C. Следовательно, точка С1 совместится с точкой C. Значит, сторона A1С1 совместится со стороной AC, а сторона B1C1 — со стороной BC. Таким образом, при наложении треугольники ABC и A1B1C1 полностью совместятся. А это означает, что ΔABC= ΔA1B1C1 (по определению). Что и требовалось доказать. Задача по теме " Высота, медиана и биссектриса треугольника". Отрезок СЕ является медианой ACD. Известно, что AE=2,5 см, AC=3 см, CD=4 см. Найдите периметр треугольника ACD. Билет № 8 Треугольник (определение). Равные треугольники. Существование треугольника, равному данному. Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника. Соединяющие вершины отрезки называются сторонами треугольника. Треугольник обозначается указанием его вершин. Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. Каков бы ни был треугольник, существует треугольник, равный данному, отложенный в треугольника, равного данному. заданном направлении, относительно заданной полупрямой. Третий признак равенства треугольника. (Третий признак равенства треугольников — по трём сторонам) Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны. 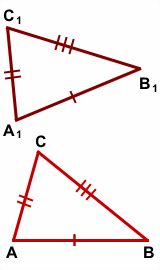 Дано: Дано:ΔABC, ΔA1B1C1, AB=A1B1, AC=A1C1, BC=B1C1. Доказать: ΔABC= ΔA1B1C1 Доказательство: Приложим треугольник A1B1C1 к треугольнику ABC так, чтобы вершина A1 совместилась с вершиной A, вершина B1 совместилась с вершиной B, точки C1 и C лежали по разные стороны от прямой AB. При этом возможны три случая взаимного расположения луча CC1 и угла ACB. 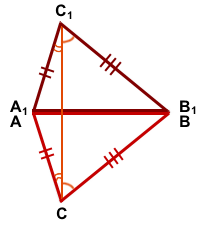 I. Луч CC1 проходит внутри угла ACB. I. Луч CC1 проходит внутри угла ACB.Проведём отрезок CC1. По условию AC=A1C1 и BC=B1C1, поэтомутреугольники ACC1 и BCC1 — равнобедренные с основанием CC1. По свойству равнобедренного треугольника, ∠ACC1=∠AC1C и ∠BCC1=∠BC1C. Если к равным углам прибывать равные углы, то получим равные углы: 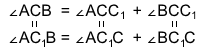 Таким образом, ∠ACB=∠AC1B. Точки A1 и A, B1 и B совмещены, то есть ∠AC1B и ∠A1C1B1 — один и тот же угол. Для треугольников ABC и A1B1C1 имеем: AC=A1C1, BC=B1C1 (по условию), ∠ACB=∠A1C1B1 (по доказанному). Следовательно, ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).  II. Луч CC1 проходит внутри угла ACB. II. Луч CC1 проходит внутри угла ACB.Так как AC=A1C1 и BC=B1C1, треугольники ACC1и BCC1 — равнобедренные с основанием CC1 и ∠ACC1=∠AC1C и ∠BCC1=∠BC1C (как углы при основании). Если из равных углов вычесть равные углы, то получим равные углы: 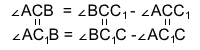 Таким образом, ∠ACB=∠AC1B и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).  III. Луч CC1 совпадает со стороной угла ACB. III. Луч CC1 совпадает со стороной угла ACB.По условию BC=B1C1, поэтому треугольник BCC1 — равнобедренный с основанием CC1. Отсюда ∠C1=∠C (как углы при основании) и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников). Что и требовалось доказать. Задача по теме "Неравенства треугольника". Существует ли треугольник со сторонами 7 см, 2 см и 10 см? Ответ обоснуйте. Билет № 9 Углы, образованные при пересечении двух прямых секущей. Аксиома параллельности прямых (без доказательства) При пересечении прямых секущей образуются такие пары углов: Углы, лежащие между прямыми и по одну сторону секущей, называются внутренними односторонними углами. Углы, лежащие между прямыми и по разные стороны от секущей, называются внутренними разносторонними углами. Углы, лежащие по одну сторону секущей, но один из них лежит между заданными прямыми, а другой не лежит между ними, называются соответствующими.  Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной Внешний угол треугольника (определение). Теорема о внешнем угле треугольника. Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним Доказательство. Пусть ABC – данный треугольник. По теореме о сумме углов в треугольнике
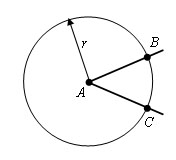
3. Задача по теме "Признаки равенства прямоугольных треугольников". У треугольников ABC и DEK: 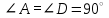 , AC=DK, AB=DE. Докажите, что , AC=DK, AB=DE. Докажите, что  . . Билет № 10 Прямоугольный треугольник. Признаки равенства прямоугольных треугольников (без доказательства). Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов) Признак равенства прямоугольных треугольников по двум катетам  Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны. Признак равенства прямоугольных треугольников по катету и гипотенузе  Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны. Признак равенства по гипотенузе и острому углу  Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны. Признак равенства прямоугольных треугольников по катету и острому углу 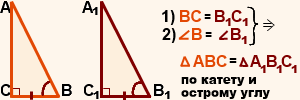 Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны. Параллельные прямые (определение). Признаки параллельности двух прямых (доказательство одного из них). Две прямые a и b на плоскости, которые не пересекаются, называются параллельными и обозначаются a∥b. Признак 1: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Доказательство: Через точку К - середину отрезка секущей - проведем перпендикуляр к прямой b - КН, продлим его до пересечения с прямой а. АК = КВ, так как К середина АВ, углы при вершине К равны как вертикальные, ∠КВН = ∠КАН' по условию, ⇒ ΔВКН = ΔАКН' по стороне и двум прилежащим к ней углам. Значит ∠АН'К = ∠ВНК = 90°. Обе прямые а и b перпендикулярны третьей прямой НН', значит они параллельны. Признак 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Доказательство: ∠1 = ∠2 по условию (соответственные углы) ∠3 = ∠1 как вертикальные, ⇒ ∠2 = ∠3, а это накрест лежащие углы, значит прямые параллельны по первому признаку. Признак 3: Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны. Доказательство: ∠1 + ∠2 = 180° по условию (односторонние углы), ∠2 + ∠3 = 180° так как эти углы смежные, значит ∠1 = ∠3, а это накрест лежащие углы, значит прямые параллельны по первому признаку.  3. Задача по теме " Угол. Измерение углов". Известно, что  =90º. Луч OD делит угол AOB на два угла: =90º. Луч OD делит угол AOB на два угла: 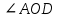 и и 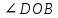 . Найдите . Найдите 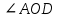 , если угол AOD в два раза меньше угла DOB. , если угол AOD в два раза меньше угла DOB.Билет № 11 1.Окружность (определение). Радиус, хорда, диаметр окружности. Окружность-это геометрическая фигура, состоящая из множества точек, находящихся на одинаковом расстоянии от точки, называемой центром окружности. Радиус- это отрезок, соединяющий центр окружности и любую точку окружности. Диаметр-это отрезок, соединяющий две точки окружности и проходящий через центр. Хорда- это отрезок, соединяющий две любые точки окружности. Треугольник (определение). Теорема о сумме углов треугольника. Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Сумма углов треугольника равна 180 градусам
Задача по теме "Свойство катета, лежащего против угла в 30º". В треугольнике ABC  =90º, =90º, 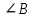 =60º, AB=3,7 см. Найдите длину отрезка BC. =60º, AB=3,7 см. Найдите длину отрезка BC.Билет № 12 Высота, биссектриса, медиана треугольника (определения). Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса - это отрезок, делящий угол треугольника на две равные части. Высота треугольника - это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение. Построение треугольника по трём сторонам. Даны три отрезка, требуется построить из них треугольник. Данная задача является задачей на построение, для решения которой требуется циркуль и линейка. При этом следует помнить, что не из каждых трех отрезков можно построить треугольник. Как известно, любая сторона треугольника должна быть меньше суммы двух остальных. Поэтому если один из данных отрезков длиннее, чем два других вместе взятые, то при построении они просто уложатся на первом отрезке, и треугольника не получится. Алгоритм построения треугольника по трем сторонам сводится к следующему: Рисуется прямая. На ней откладывается отрезок, равный одной из данных сторон. Это можно сделать как циркулем, так и линейкой. Строится окружность (или ее часть) радиусом, равным второму отрезку, и с центром в одной из точек, отложенной на прямой. Строится окружность (или ее часть) радиусом, равным третьему отрезку, и с центром во второй из точек, отложенных на прямой. К точке пересечения окружностей проводятся отрезки из точек на прямой. Если были построены не маленькие части окружностей, то таких точек может оказаться две. Отрезки надо проводить лишь к одной любой из них. В результате получается треугольник, стороны которого равны данным отрезкам. Действительно, ведь одна из его сторон была отмерена на прямой по одному из данных отрезков, а две другие — радиусы, которые равны второму и третьему заданным отрезкам. Задача по теме "Внешний угол треугольника". В треугольнике ABC 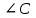 =40º, внешний угол при вершине B равен 70º. Найдите остальные внутренние углы треугольника. =40º, внешний угол при вершине B равен 70º. Найдите остальные внутренние углы треугольника.Билет № 13 Перпендикулярные прямые (определение). Перпендикуляр к прямой. Две прямые называются перпендикулярными, если они пересекаются под прямым углом . Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра. Построение биссектрисы угла.  Построить биссектрису данного угла.
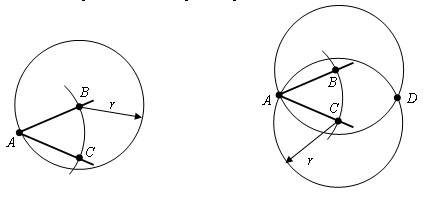 Из точек В и С проведем окружности тем же радиусом r. Пусть точка D – точка их пересечения отличная от A. 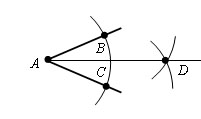 Проведем луч AD.  Проведем отрезки BD и CD. Δ ABD = Δ ACD, по третьему признаку равенства треугольников. Отсюда ∠ BAD = ∠ CAD и следовательно AD – биссектриса угла BAC. 3. Задача по теме "Свойства равнобедренного треугольника". В равнобедренном треугольнике ABC AE – высота, BC- основание. Известно, что BC=12,8 см. Найдите длину отрезка CE. Билет № 14 Виды треугольников по величине углов.
Деление отрезка пополам.
Задача по теме " Смежные углы". Найдите смежные углы, если один из них в два раза больше другого. Билет № 15 Расстояние от точки до прямой. Расстояние между параллельными прямыми. Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на данную прямую. Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой. Поэтому, чтобы найти расстояние между параллельными прямыми, надо: 1) выбрать на одной из параллельных прямых точку; 2) опустить из выбранной точки к другой прямой перпендикуляр; 3) найти длину этого перпендикуляра. Неравенство треугольника. Теорема. Каждая сторона треугольника меньше суммы двух других сторон. Доказательство. Рассмотрим произвольный треугольник ABC и докажем, что AB
1 2 |