билеты. Билет + ответы по геом. Билет 1 Виды треугольников по длине сторон. Периметр треугольника

• Название: Билет 1 Виды треугольников по длине сторон. Периметр треугольника
• Анкор: билеты
• Дата: 23.11.2022
• Размер: 488.58 Kb.
• Имя файла: Билет + ответы по геом.docx
• Тип: Документы; #808023
• страница: 2 из 2

Следствие.
Для любых трех точек A, B и С, не лежащих на одной прямой, справедливы неравенства: AB < AC + CB, AC < AB + BC, BC < BA + AC. 

3. 
   Задача по теме " Взаимное расположение окружностей".
   

Две окружности диаметром 4 и 8 см касаются внешним образом. Найдите расстояние между центрами этих окружностей.
Билет № 16

1. 
   Равносторонний треугольник. Свойства равностороннего треугольника
   

Треугольник называется равносторонним, если все его стороны равны.

Свойства

В равностороннем треугольнике все углы равны между собой и равны 60⁰:

В равностороннем треугольнике высоты, биссектрисы, медианы и пересекаются в одной точке, которая называется центром равностороннего треугольника.

2. 
   Теорема о соотношении между сторонами и углами треугольника.
   

Теорема

В треугольнике:

1) против большей стороны лежит больший угол;

1) против большего угла лежит большая сторона.

1) Дано: ∆ ABC, AC>AB.

Доказать: ∠B>∠C.

Доказательство: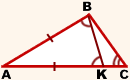

Отложим на стороне AC отрезок AK: AK=AB.

Так как AC>AB, то точка K лежит между точками A и C. Следовательно, ∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.

Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.

Значит, у него углы при основании равны: ∠ABK=∠AKB.

Для треугольника BCK  ∠AKB — внешний.

Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.

Имеем: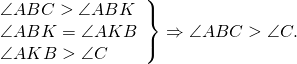

  

2) Дано: ∆ ABC,

∠B>∠C.

Доказать: AC>AB.

Доказательство:

(методом от противного).Предположим, что неравенство AC>AB — неверное. Тогда либо AC=AB, либо ACAB.

Что и требовалось доказать.

3. 
   Задача по теме "Смежные и вертикальные углы ".
   

Сумма данного угла и вертикального ему угла равна 60º. Найдите величину вертикального и смежных с ним углов.

Билет № 17

1. 
   Равносторонний треугольник. Свойства равностороннего треугольника.
   

Треугольник называется равносторонним, если все его стороны равны.

Свойства

В равностороннем треугольнике все углы равны между собой и равны 60⁰:

В равностороннем треугольнике высоты, биссектрисы, медианы и пересекаются в одной точке, которая называется центром равностороннего треугольника.

3. 
   Вертикальные углы (определение). Свойства вертикальных углов
   

Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого


3. Задача по теме "Отрезок. Измерение отрезков ".

На отрезке OD, длина которого 24 см, отмечена точка A. Найдите длину отрезка AD, если отрезок OA на 8 см длиннее отрезка AD.

Билет № 18

1. 
   Прямоугольный треугольник (определение). Катет. Гипотенуза. Свойства прямоугольного треугольника (без доказательства)
   

Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами прямоугольного треугольника, а сторона, противолежащая прямому углу – гипотенузой прямоугольного треугольника.

1. Сумма острых углов равна 90
2. Катет лежащий против угла 30 равен половине гипотенузы
3. Обратная теорема: Если катет равен половине гипотенузы, то угол, лежащий против него равен 30

2. Построение угла, равному данному.

 Отложить от данного луча угол, равный данному.

Решение. Данный угол с вершиной А и луч ОМ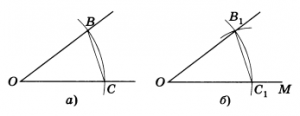



Проведем произвольную окружность с центром в вершине О данного угла. Пусть В и С — точки пересечения окружности со сторонами угла (рис а). Радиусом ОВ проведем окружность с центром в точке О — начальной точке данного луча (рис. б). Точку пересечения этой окружности с данным лучом обозначим С₁. Опишем окружность с центром С₁ и радиусом ВС. Точка В₁ пересечения двух окружностей лежит на стороне искомого угла. Это следует из равенства Δ ОBC = Δ ОВ₁С₁(третий признак равенства треугольников).

2. 
   Задача по теме "Внутренние и внешние углы треугольника ".
   

Один из внешних углов прямоугольного треугольника равен 130º. Найдите острые углы треугольника
Билет № 19

1. 
   Отрезок (определение). Длина отрезка. Основное свойство измерения отрезков.
   

Отрезок - это часть прямой, которая ограничена двумя точками, т.е. она имеет начало и конец, а значит можно измерить её длину

Расстоянием между двумя точками называется длина отрезка . 

1.Каждый отрезок имеет определенную длину, большую нуля. 

2.Длина отрезка равняется сумме длин частей, на которые он разбивается любой своей внутренней точкой. 

3.При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю. 

4.Два отрезка называются равными, если равны их длины.

2. 
   Теорема о соотношении между сторонами и углами треугольника.
   

Теорема

В треугольнике:

1) против большей стороны лежит больший угол;

1) против большего угла лежит большая сторона.

1) Дано: ∆ ABC, AC>AB.

Доказать: ∠B>∠C.

Доказательство:

Отложим на стороне AC отрезок AK: AK=AB.

Так как AC>AB, то точка K лежит между точками A и C. Следовательно, ∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.

Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.

Значит, у него углы при основании равны: ∠ABK=∠AKB.

Для треугольника BCK  ∠AKB — внешний.

Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.

Имеем: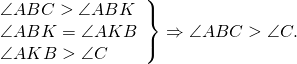

  

2) Дано: ∆ ABC,

∠B>∠C.

Доказать: AC>AB.

Доказательство:

(методом от противного).Предположим, что неравенство AC>AB — неверное. Тогда либо AC=AB, либо ACAB.

Что и требовалось доказать.

3. 
   Задача по теме "Виды треугольников ".
   

Периметр равностороннего треугольника DEK равен 18 см. Найдите стороны треугольника DEK .
Билет № 20

1. Угол (определение). Развернутый угол. Внутренняя и внешняя область угла.

Основное свойство откладывания углов.

Угол — это геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.

Лучи называются сторонами угла, а их общее начало — вершиной угла.

Развернутый угол — это угол, стороны которого лежат на одной прямой.Градусная мера развёрнутого угла равна 180º.Каждая сторона развернутого угла дополняет другую сторону до прямой, то есть стороны развёрнутого угла являются дополнительными лучами. Угол разделяет плоскость на две части, каждая из которых также называется углом, то может возникнуть неоднозначность в том, какой именно из углов рассматривается. Чтобы наглядно показать, о каком именно угле идёт речь, на чертеже обычно делается какое-нибудь специальное обозначение.

Тот из углов, который рассматривается, на чертеже обычно отмечают дугой, проведённой от одной стороны угла до другой:

Часть плоскости, расположенная между сторонами рассматриваемого угла называется внутренней областью угла. Часть плоскости не принадлежащая рассматриваемому углу называется внешней областью угла:

От любой полупрямой в заданную  полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°,и только один.

3.Теорема о существовании и единственности перпендикуляра к прямой.

Теорема. 

Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один. 

Доказательство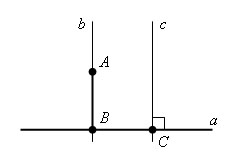 

 

Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через какую-нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a. 
Значит отрезок AB ⊥ a. 
Теперь докажем единственность перпендикуляра AB.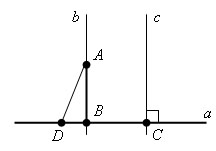 

 

Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a. 
Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как сумма всех углов в треугольнике 180 °. Теорема доказана.

3. Задача по теме "Сумма углов треугольника ".

Углы треугольника DKC относятся как 2:4:3. Найдите углы треугольника DKC.