Шпоры по гидравлике. Билет Легкоподвижность (текучесть) жидкой среды. В чем она проявляется
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
3. Гипотеза Буссинеска… Полуэмпирическая теория турбулентности начала свое развитие с работ Буссинеска. Из закона трения жидкостей Ньютона: В отличии от физической вязкости () турбулентная вязкость (m ) не является свойством жидкости и в турбулентном потоке переменна. В 1904г. Прандтль предложил 2-х сложную модель турбулентности согласно ей в непосредственной близости от стенки область вязкого подслоя с ламинарным течением: в= du/dy, а m =0. В части потока, удаленного от стенки, наоборот, m = du/dy, а в =0. Более поздние исследования показали, что есть некоторая область, где эти напряжения имеют один порядок: =в +m =( + m) du/dy. Билет 28. 2. Уравнение движения жидкости в напряжениях. Запишем для произвольного жидкого объема V, ограниченного поверхностью F, уравнение, выражающее теорему о количестве движения системы: производная по времени от количества движения системы равна сумме действующих на нее внешних сил. Т.к. количество движения Следовательно, уравнение количества движения жидкого объема V запишется в виде: Получим векторную форму уравнения движения в напряжениях в виде: В проекциях на координатные оси это запишется так: 3. Гидравлический удар в трубопроводах. Формулы Жуковского и Мишо. Гидравлический удар - изменение давления при резком изменении скорости движения в трубах, вся кинетическая энергия превращается в энергию давления. Чаще всего возникает при быстром закрытии (открытии) задвижки. Фазы развития гидравлического удара: 1.остановка движения жидкости ; давление: р + рударное; с - скорость ударной волны в сторону противоположную движению жидкости; 2. расширение трубы; давление: р + рударное; изменение направления движения жидкости ; 3. частичное сужение трубы до начальных размеров; давление: р + рударное; изменение направления ударной волны ; направление движения жидкости ; 4. полное сужение трубы до начальных размеров; давление: р + рударное; направление движения жидкости ; 5. частичное сужение трубы; давление: р - рударное; 6. полное сужение трубы; давление: р - рударное; 7.расширение трубы до начальных размеров; давление: р0; скорость жидкости равна нулю. График давления аналогичный графику затухающих колебаний. Борьба с гидравлическим ударом: уменьшение фазы удара T = 2L/c; увеличение времени остановки жидкости; уравнительные баки; гидроаккумуляторы гасящие ударную волну; предохранительные клапаны. Если tзакр< 2l/Uуд, волна пониженного давления, отраженная от резервуара, не успевает прийти к задвижке до его закрытия и получается прямой механический удар. Повышенное давлении определим по формуле Жуковского: pуд = Waуд. Если tзакр> 2l/Uуд, то давление не достигнет максимальной величины, т.к. частично погашается отраженной волной пониженного давления, возвращаясь к задвижке от резервуара раньше, чем будет закрыты задвижка. В этом случае будет непрямой гидроудар. Повышенное давлении определим по формуле Мишо: pуд = W2l/tзакр. Билет 30. 1. Ротор (вихрь) скорости и его физический смысл при описании движения жидкой среды. Векторное произведение оператора ▼ на вектор скорости называется ротором или вихрем скорости. Физически вихрь скорости представляет собой вектор удвоенной скорости вращения частицы жидкости. Если ротор не равен нулю, то имеет место вращение элементарного объема. Такое течение называется вихревым. В противном случае течение безвихревое. 2. Теорема Томпсона (Кельвина) (без доказательств) и следствие из нее. Теорема Томпсона (законом сохранения циркуляции скорости) утверждает, что если 1) силы, действующие в жидкости имеют потенциал; 2) идеальная жидкость баротропна; 3) поле скоростей непрерывно, то циркуляция скорости по любому замкнутому жидкому контору остается постоянной во все время движения жидкости: dГ/ dt =0. Следствие (теорема Лагранжа): если соблюдаются условия теоремы Томпсона и вихрей не было, то они и не могут появиться, а если были то не могут исчезнуть. Если условия теоремы нарушаются, то вихри смогут возникать и исчезать. Основная ценность т.Т.: позволяет объяснить причины перехода движения жидкости из безвихревого в вихревое состояние, и наоборот. Билет 32. 1. Конфузорный и диффузорный каналы. Идеальное сопло. Максимальная скорость истечения из идеального суживающегося сопла. Конфузорные течения устойчивы (сужение каналов) – в них не причин для возникновения вихрей. Вихри образуются лишь в цилиндрической трубе на выходе из конфузора. Для устранения этих вихреобразований коническую часть следует сопрягать с цилиндрической плавной кривой. Сопло Витошинского. На выходе из этого сопла поле скоростей близко к равномерному, а потери минимальны. Т.к. потери в таком сопле обусловлены трением, то коэффициент местных потерь зависит от числа Рейнольдса и отношения площадей F1/F2 и колеблется в пределах ξ=0,01…0,1. Меньшие значения соответствуют большим числам Рейнольдса. Истечение через диффузорный , т.е. расширяющийся насадок. Добавление к такой стенке с отверстием диффузорного насадка вызывает снижение давления p2
Числа подобия: Число Фруда характеризует отношение сил инерции к силам тяжести и является критерием подобия по влиянию силы тяжести жидкости. Число Эйлера представляет собой отношение давления жидкости p к удвоенному характерному скоростному напору W2/2. Для сжимаемой жидкости число Эйлера можно представить: Число Рейнольдса – параметр, характеризующий отношение сил инерции к силам вязкости. При малых Re преобладают силы вязкости, а при больших Re –силы инерции. Число Струхаля – характеризует отношение локальной инерционной силы к конвективной и является критерием, определяющим меру нестационарности течения. Числа подобия, получ. из ур-ий, опис. движение жид-ти с начал. и гранич. усл., обеспеч. однозначное выделение рассматр. явления из целого класса задач, наз. критериями подобия. | Билет 3.
Единственное условие безвихревого движения является отсутствие вращения жидких частиц относительно собственных осей. При этом частица могут двигаться по любым траекториям и деформироваться. Математическое выражение: Т.о. в случае безвихревого течения имеет место потенциал, т.е.функцию координат (x, y, z), частные производные которой по любому направлению n и, след-но, по координатным осям равны соответствующим проекциям вектора скорости: потенциал скорости полностью определяет поле скоростей: Поэтому безвихревое течение жидкости называют также потенциальным. 3. Трубка тока. Струйка тока. Поток жидкости, живое сечение, поперечное сечение, смоченный периметр. Гидравлический диаметр. Поверхность, образованная линиями тока и проходящая ч/з точки замкнутого контура, называется трубка тока. Линия тока – в каждой точке вектор тока касательный. ( Если периметр охватывает малую площадку, трубку называют элементарной). Жидкость внутри – элементарная струйка или струйка. В пределах поперечного сечения элементарной струйки скорость течения и др. параметры принимаются постоянными. Поток жидкости – совокупность элементарных струек. Струйки в потоке плотно прилегают друг к другу. Живым сечением называется сечение потока. Каждая элементарная площадка которого нормальна к соответствующему вектору скорости. Если линии тока параллельны, то живое сечение плоское. Гидравлический радиус Гидравлический диаметр Поперечным сечением потока называется сечение площадью S, перпендикулярное оси. Объемным расходом жидкости Q называется объем жидкости, протекающий через данную поверхность в секунду: Поток жидкости - конечный движущийся объем жидкости, состоящий из бесконечно большого числа элементарных струек. Билет 6. 1 Местные потери и коэффициент местного сопротивления. Сети трубопроводов, распределяющие или отводящие жидкость от потребителей, меняют свой диаметр (сечение); на сетях устраиваются повороты, ответвления, устанавливаются запорные устройства и т. п. В этих местах поток меняет спою форму, резко деформируется. Вследствие изменения формы возникают дополнительные силы сопротивления, так называемые местные сопротивления. На их преодоление расходуется напор. Напор, затрачиваемый на преодоление местных сопротивлений, называют местными потерями напора и обозначают через Местные потери напора определяют как произведение скоростного напора непосредственно вблизи местного сопротивления Общей теории для определения коэффициентов местных сопротивлений, за исключением отдельных случаев, нет. Поэтому коэффициенты местных сопротивлений, как правило, находят опытным путем. Значения их для различных элементов трубопроводов приводятся в технических справочниках. Иногда местные сопротивления выражают через эквивалентную длину прямого участка трубопровода 3. Моделирование физических процессов. Способы установления критериев подобия. Моделирование различных физических процессов исходит из подобия рассматриваемых явлений. Два явления называются подобными, если по известным параметром одного из них можно определить параметры второго простым пересчетом. Условиями подобия двух явлений являются равенства некоторых безразмерных комплексов, называемых критериями (числами) подобия. Существует два способа установления критериев подобия: один из них называют теорией подобия, а другой – методом анализа размерностей. Метод подобия используется в том случае, когда исследуемое физическое явление может быть описано дифференциальными уравнениями. В этом случае числа подобия легко определяются как коэффициенты уравнений, представленных в безразмерном виде. Если физическое явление не имеет математического описания, определение чисел подобия производится методом анализа размерностей. Степень сложности уравнений при использовании метода подобия не имеет значения, т.к. для нахождения чисел подобия решение уравнений не требуется. Анализ размерностей позволяет установить систему безразмерных критериев, характеризующих данное физическое явление. В основе анализа размерностей лежит тот факт, что уравнения, описывающие физические явления, подчиняются правилу равенства размерностей всех слагаемых в уравнении. Определение критериев подобия посредством анализа размерностей на π-теореме. которая доказывает возможность перехода от соотношений между размерными величинами и эквивалентным безразмерным степенным соотношением. Билет 10. 1. Рабочая точка насосной установки. Характеристика насоса – это зависимость полезной работы насоса от расхода жидкости Hнас = f2(Q) при постоянной частоте вращения вала насоса. Установившийся режим работы гидравлической системы с насосной подачей определяется точкой пересечения характеристики трубопровода Hпотр=f(Q) и характеристики насоса Ннас=f2(Q), которая называется рабочей точкой и соответствует условию Hпотр= Ннас. Во время работы такой режим устанавливается и поддерживается автоматически. Режимы работы двигателей и вместе с ними расходы топлива изменяются в широком диапазоне. Поэтому топливные системы снабжаются системами регулирования, позволяющими смещать рабочие точки на меньшие и большие расходы. 2. Связь между характерными и безразмерными скоростями. Максимальная скорость истечения (Wmax). При энергетически изолированном течении скорость Wmax будет получена тогда, когда полная энтальпия целиком будет превращена в кинетическую энергию, т.е. когда газ расширится до абсолютного вакуума T=0, p=0 и =0: 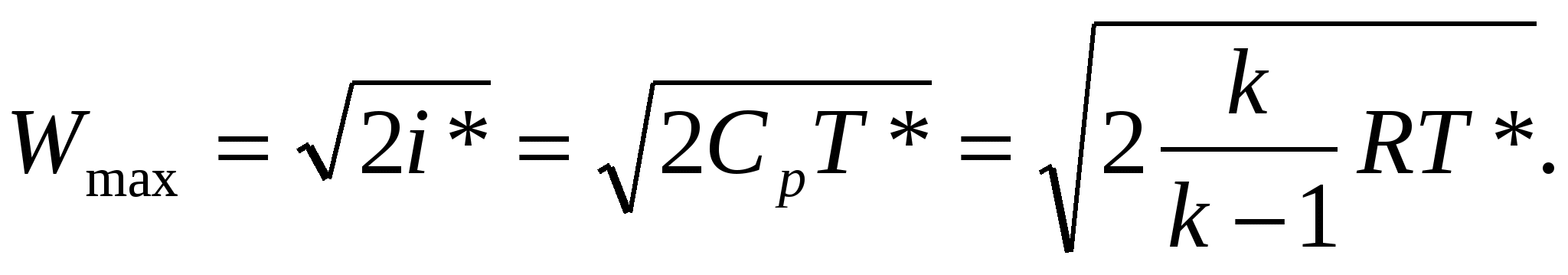 Критической называется скорость потока, равная местной скорости звука. При критическом (звуковом) течении все параметры потока называются критическими. Критическая скорость устанавливается при израсходовании на ускорение газа лишь определенной части полного теплосодержания: 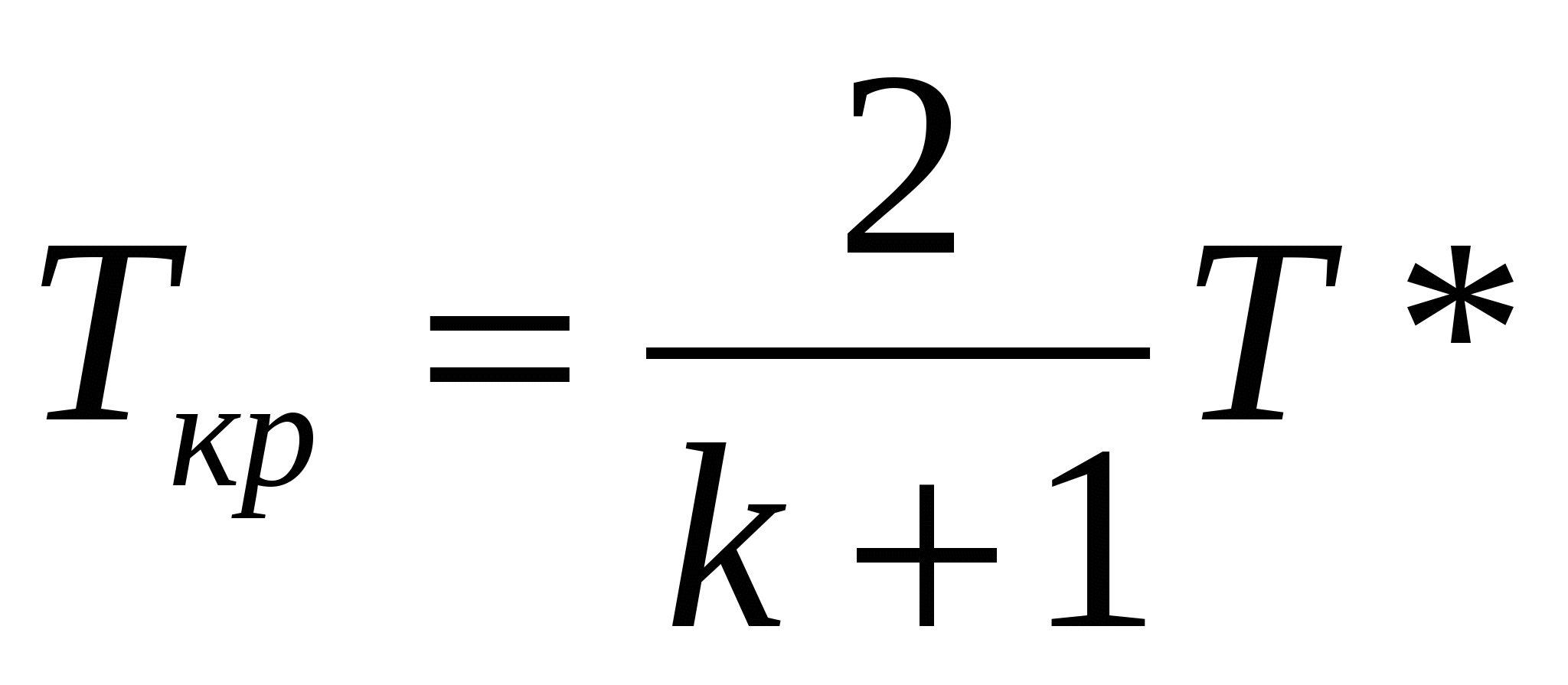 ; критическая скорость звука: ; критическая скорость звука: 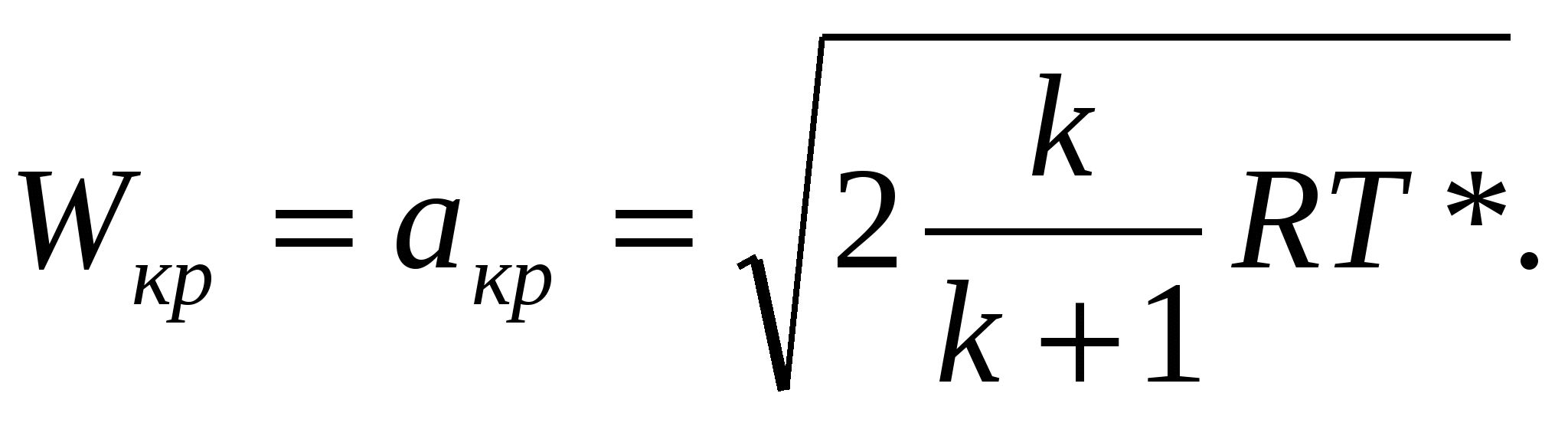 , т.е. величина критической скорости звука в данном газе определяется только температурой его торможением. , т.е. величина критической скорости звука в данном газе определяется только температурой его торможением.Безразмерная скорость – отношение скости потока к максимальной скорости: Λ = W/ Wmax . Приведенная скорость – отношение скорости потока к критической скорости звука: λ = W/ aкр. Физический смысл чисел: М, λ, Λ. 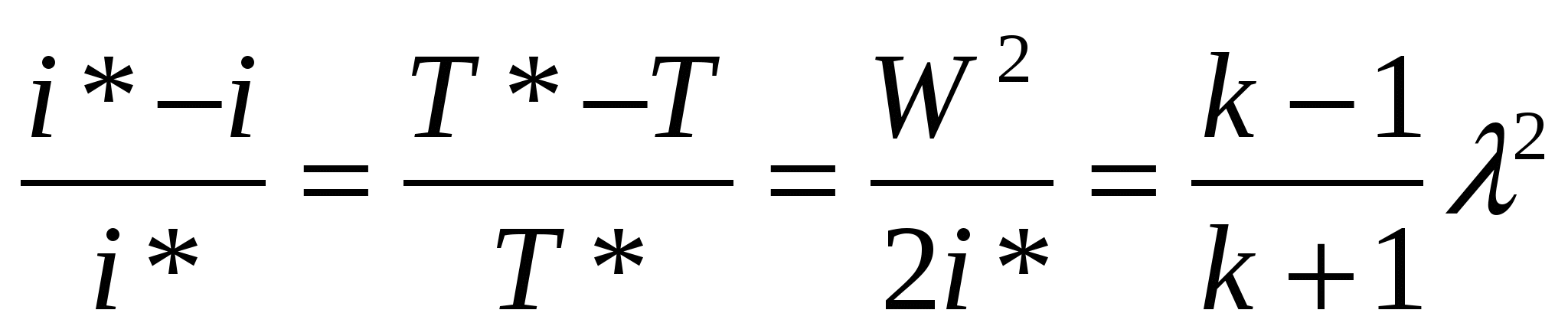 ; ; Числа М, λ и Λ характеризуют степень преобразования полной энтальпии газа в его кинетическую энергию в данной точке любого потока, т.е. имеют одинаковый физический смысл. Поэтому между М, λ, Λ существует однозначная связь и задание одного ихз них определяет два других. |
