Шпоры по гидравлике. Билет Легкоподвижность (текучесть) жидкой среды. В чем она проявляется

• Название: Билет Легкоподвижность (текучесть) жидкой среды. В чем она проявляется
• Анкор: Шпоры по гидравлике.doc
• Дата: 02.05.2017
• Размер: 0.89 Mb.
• Имя файла: Шпоры по гидравлике.doc
• Тип: Документы; #6683
• Категория: Промышленность. Энергетика
• страница: 2 из 7

Билет 22.

1. Эквипотенциальные поверхности и их взаимосвязь с линиями тока.

Эквипотенциальные поверхности и линии – это поверхности для пространственного и линии для плоского движений жидкости, для которых потенциал скорости имеет постоянное значение  = С, d = 0.

Дифференциальное уравнение эквипотенциальных поверхностей в пространстве x, y, z:



Т.к. , а grad –вектор, направленный по нормали к линии постоян. значения скалярной функции, то во всех точках эквипотенциальной поверхности или линии =const вектор W к ней ортогонален. Т.к. вектор скорости всегда касателен к линии тока, то линии тока всегда ортогональны к эквипотенциальным поверхностям или линиям.
3. Особенности турбулентного режима движения жидкости. Пристенная и струйная турбулентность.

При Re>Re_кр в жидкости возникают вихри, это конечные объемы жидкости (конгломераты), которые вследствие различных причин движутся произвольным образом в пространстве занятом течением – вихревые моли. Вихревые моли зарождаясь у стенок трубы (пристенная турбулентность) и внутри потока (струйная турбулентность) своим перемещением нарушают существовавшее до того упорядоченное движение , характерное для ламинарного режима.

Траектории частиц, проходящих через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, несмотря на прямолинейность трубы. Турбулентное течение всегда является неустановившемся, т.к. значения скоростей и давлений, а также траектории частиц, изменяются со временем. Но его можно считать установившимся при условии, что осредненные по времени значения скоростей и давлений, а также расход потока не изменяются со временем. Распределение скоростей при турбулентном течении более равномерное, а нарастание скорости у стенки более крутое, чем у ламинарного, для которого характерен параболический закон распределения скоростей.

В турбулентном потоке потери напора на трение по длине значительно больше, чем при ламинарном течении при тех же размерах трубы, расходе и вязкости жидкости.
Билет 24.

1. Особенности профиля скоростей в пограничном слое на стенке и в свободной струе.

Рассмотрим характер распределения скоростей в сечении потока при ламинарном и турбулентном режимах движения жидкости. Как показали теоретический анализ и опыты при ламинарном режиме движения жидкости в круглой трубе, скорости в поперечном сечении распределены по параболе (рис. 1), скорости у стенок трубы равны нулю и, плавно увеличиваясь, достигают максимума на оси потока.

П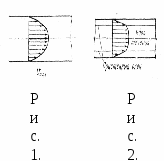
ри ламинарном режиме движения существуют лишь продольные составляющие скоростей. В этом случае силы сопротивления движению возникают вследствие трения между слоями жидкости, т. е. зависят от вязкости жидкости и не зависят (почти) от состояния стенок.

При турбулентном режиме закон распределения скоростей по живому сечению более сложен; в большей части сечения скорости близки к средней и резко падают в тонком слое у стенок, доходя до нуля. График распределения скоростей по сечению близок к трапеции (рис. 2). Такое распределение скоростей вызывается турбулентным перемешиванием в результате поперечных перемещений частиц. Быстро движущиеся частицы жидкости из средней части потока сталкиваются с медленно движущимися частицами вблизи стенок, благодаря чему и происходит выравнивание скоростей. И только в пограничном слое, где стенки препятствуют перемешиванию, скорость резко убывает.

2. π-теорема анализа размерностей.

Анализ размерностей позволяет установить систему безразмерных критериев, характеризующих данное физическое явление. В основе анализа размерностей лежит тот факт, что уравнения, описывающие физические явления, подчиняются правилу равенства размерностей всех слагаемых в уравнении.

Определение критериев подобия посредством анализа размерностей на π-теореме, которая доказывает возможность перехода от соотношений между размерными величинами и эквивалентным безразмерным степенным соотношением.

Π-терема: Пусть размерная величина а является функцией независимых одна от другой размерных величин a=f(a₁, a₂,…, a_k, a_k+1, …, a_n ), из которых a₁, a₂,…, a_k имеют независимые размерности. Тогда, обозначая через π с соответствующим индексом безразмерные степенные комбинации одной из зависимых величин a, a_к+1,…, a_n, с независимыми, можно показать, что π=( (π₁, π₂,…, π_n-k) или ( (π₁, π₂,…, π_n-k)=0. Общее число безразмерных комплексов равно n-k+1. Каждый из них является комбинацией k+1 размерных величин и может быть представлен в виде …, где показ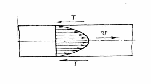атели m1,m2,…,mk определяются из анализа размерности величины a. Анализ размерностей устанавливает только сам факт взаимосвязи между критериями. Вид функций  и  определяется из эксперимента или теоретически.
Билет 27.

1. Принципы учета гидравлических потерь при расчете реальных течений в трубах.

Гидравлические потери – потери механической энергии напора в результате ее необратимого перехода в теплоту, имеющие место при движении реальной жидкости и связанные с проявлением /преодолением сил сопротивления.

Для преодоления сил гидравлического трения и сохранения поступательного движения жидкости необходимо приложить силу, направленную в сторону движения и равную силам сопротивления. Работу этой силы называют потерями напора по длине потока (путевые потери напора) и обозначают через .

Сети трубопроводов, распределяющие или отводящие жидкость от потребителей, меняют свой диаметр (сечение); на сетях устраиваются повороты, ответвления, устанавливаются запорные устройства и т. п. В этих местах поток меняет спою форму, резко деформируется. Вследствие изменения формы возникают дополнительные силы сопротивления, так называемые местные сопротивления. На их преодоление расходуется напор. Напор, затрачиваемый на преодоление местных сопротивлений, называют местными потерями напора и обозначают через .

Общие потери напора равны сумме потерь напора по длине и местных

. (81)

Размерность потерь напора такая же, как и напора, т. е. метры столба жидкости.
2. Интегральная форма закона сохранения количества движения.

Уравнение количества движения жидкого объема V запишется в виде: (1) , где и - суммы внешних массовых и поверхностных сил, действующих на жидкий объем V и поверхность F соответственно.

Рассмотрим установившееся движение произвольного жидкого объема V, ограниченного поверхностью F. Пусть за время dt поверхность F перемещается в положение F . На поверхности F выделим элементарную площадку dF, которая за время dt перемещается в положение dF . Между этими площадками образуется элементарный косой цилиндр. Для этого цилиндра количество движения равно: (1). Знак этого выражения положителен, если жидкость вытекает из контрольного объема и отрицателен, если она втекает в контрольный объем. Поэтому, если взять интеграл по поверхности F от выражения (1), то, при учете правила знаков, получим изменение количества движения объема V за время dt, т.е.

. Тогда исходное уравнение запишется в виде:.

Оно часто называется первым уравнением Эйлера или уравнением импульсов и формируется так: при установившемся движении жидкого объема равнодействующая внешних сил, действующих на него, равна по величине и направлению потоку количества движения (изменению секундного количества движения) через контрольную поверхность.

В общем случае неустановившегося движения необходимо учитывать и локальную часть индивидуальной производной. Тогда уравнение импульсов запишется так:

3. Порядок расчета простого трубопровода.

Основным элементом любой трубопроводной системы, какой бы сложной она ни была, является простой трубопровод. Классическим определением: простым трубопроводом является трубопровод, собранный из труб одинакового диаметра и качест­ва его внутренних стенок, в котором движется транзитный поток жидкости, и на котором нет местных гидравлических сопротивлений.

При напорном движении жидкости простой трубопровод работает полным сечением S=4πR²= const. Размер сечения трубопровода (диаметр или ве­личина гидравлического радиуса), а так­же его протяжённость (длина) трубопровода (/, L) являются основными геометрическими характеристиками трубопровода. Основными технологическими характеристиками тру­бопровода являются расход жидкости в трубопроводе Qи напор(на головных сооруже­ниях трубопровода, т.е. в его начале). Большинство других характеристик простого тру­бопровода являются, не смотря на их важность, производными характеристиками. По­скольку в простом трубопроводе расход жидкости транзитный (одинаковый в начале и конце трубопровода), то средняя скорость движения жидкости в трубопроводе постоянна v=const. Для установившегося движения жидкости по трубопроводу средняя скорость движения жидкости определяется по формуле Шези: v=C√Ri_, где: - скоростной коэффициент Шези, R_г= S/П - гидравлический радиус сечения, для круглого сечения при полном заполнении жидкостью R_г=d/4; i=h_тр/l - гидравлический уклон. Полагая, что весь имеющийся напор на головных сооружениях (в начале) трубопро­вода тратится на преодоление сил трения в трубопроводе (в простом трубопроводе это по­тери напора по длине), уравнение движения жидкости (Бернулли) примет вид: H=²l/CR_г.

Расход жидкости в трубопроводе: Q=vS = CS√Ri .

Обозначив: SC√R=K , получим основное уравнение простого трубопровода: Q=K√i.

где: К - модуль расхода - расход жидкости в русле заданного сечения при гид­равлическом уклоне равном единице (иначе модуль расхода называют расходной характе­ристикой трубопровода). Другой и более известный вид основного уравнения простого трубопровода получим, решив уравнение относительно напора: H=Q²/K² или H=RQ²

Величину 1/K² называют удельным сопротивле­нием трубопровода, R=1/Q²- - его полным сопротив­лением

График уравнения простого трубопровода носит название его гидравлической харак­теристики. Вид гидравлической характеристики зави­сит от режима движения жидкости в трубопроводе: при ламинарном движении жидкости гидравлическая характеристика трубопровода - прямая линия, проходящая через начало координат (1). При турбулентном режиме гидравлическая характеристика - парабола (2).

Если на трубопроводе собранном из труб одинакового диаметра имеются местные сопротивления, то такой трубопровод можно привести к простому трубопроводу эквива­лентной длины l_экв: l_экв = l +d∑ξ /λ.
Билет 33.

1. Совершенный газ. Идеальный газ (жидкость).

Изучение реальных жидкостей и газов связано со значительными трудностями, т.к. физические свойства реальных жидкостей зависят от их состава, от различных компонен­тов, которые могут образовывать с жидкостью различные смеси как гомогенные (раство­ры) так и гетерогенные (эмульсии, суспензии и др.) По этой причине для вывода основ­ных уравнений движения жидкости приходится пользоваться некоторыми абстрактными моделями жидкостей и газов, которые наделяются свойствами неприсущими природным жидкостям и газам.

Идеальная жидкость - модель природной жидкости, характеризующаяся изотропно­стью всех физических свойств и, кроме того, характеризуется абсолютной несжимаемо­стью, абсолютной текучестью (отсутствие сил внутреннего трения), отсутствием процес­сов теплопроводности и теплопереноса.

Реальная жидкость - модель природной жидкости, характеризующаяся изотропно­стью всех физических свойств, но в отличие от идеальной модели, обладает внутренним трением при движении.

Совершенный газ – модель газа, молекулы которого представляются в виде материальных точек, взаимодействующих только при соударениях. Совершенный газ имеет постоянные теплоемкости С_p и С_v, показатель изоэнтропы k= С_p / С_v и молекулярную массу m и удовлетворяет уравнению состояния Клапейрона p= RT.

Идеальный газ - модель, характеризующаяся изотропностью всех физических свойств и абсолютной сжимаемостью.

Реальный газ - модель, при которой на сжимаемость газа при условиях близких к нормальным условиям существенно влияют силы взаимодействия между молекулами.

При изучении движения жидкостей и газов теоретическая гидравлика (гидромехани­ка) широко пользуется представлением о жидкости как о сплошной среде. Такое допуще­ние вполне оправдано, если учесть, что размеры пространства занимаемого жидкостью, во много раз превосходят межмолекулярные расстояния (исключением можно считать лишь разряженный газ). При изучении движения жидкостей и газов последние часто рассматри­ваются как жидкости с присущими им некоторыми особыми свойствами. В связи с этим принято различать две категории жидкостей: капельные жидкости (практически несжи­маемые тела, или собственно жидкости) и сжимаемые жидкости (газы).

Билет 2.

1 Модели жидкой среды.

В зависимости от тех свойств получают различные ее модели.

Под моделью реальной среды понимают такую гипотетическую среду, в которой учтены только некоторые из физических свойств, существенные для определенного круга явлений и технических задач. Одной из основных в гидромеханике является модель несжимаемой идеальной (или невязкой) жидкости. Так называется гипотетическая сплошная среда, обладающая текучестью, лишенная вязкости и полностью несжимаемая.

Более полно свойства реальной жидкости учитываются в модели вязкой несжимаемой жидкости, которая представляет собой среду, обладающую текучестью и вязкостью, но абсолютно несжимаемую. Теория вязкой несжимаемой жидкости лишь в ограниченном числе случаев с простейшими граничными условиями позволяет получить точные решения полных уравнений движения.

Гипотезу сплошности: упрощенные модели, представляющими собой материальный континуум, т. е. материальную среду, масса которой непрерывно распределена по объему, т.е. жидкость можно рассматривать как сплошную среду (континуум), лишенную молекул и межмолекулярных пространств.

3 Силы, действующие в жидкости. Напряжения.

Внешние силы, действующие на жидкий объем и определяющие его движение, разделяются на массовые (объемные) и поверхностные.

Массовые силы R приложены ко всем жидким частицам, составляющим жидкий объем. К ним отн. силы тяжести и силы инерции. Кроме того, к массовым силам отн. силы взаимодействия частиц токопроводящей жидкости с э/м полями. Для характеристики массовых сил вводится величина «напряжение массовых сил», которая опр. как отношение вектора массовой силы ∆R к массе ∆m жидкой частицы, на которую она действует: . В соответствии со вторым законом Ньютона, массовая сила равна произведению массы на ее ускорение, вызванное этой силой. Поэтому напряжение массовой силы равно ускорению центра массы частицы, проходящей в данный момент времени через данную точку, и характеризует распределение массовых сил в пространстве, занятом жидкостью. Проекция напряжения массовой силы на оси координат x, y, z обозначим X, Y, Z тогда .

Поверхностные силы Rn представляют воздействие внешней среды на поверхность выделенного объема. Это воздействие распределено по поверхности непрерывно. К ним отн. силы трения и давления. Нормальная составляющая поверхностной силы действует по нормали к поверхности ∆S, противоположно . Сила трения или тангенциальная составляющая действует в плоскости ∆S.

Напряжения поверхностных сил в точке А (x, y, z) –это пределы отношений соответствующих сил к площадке ∆S при стягивании ее в точку.

Билет 5.

1 Полный импульс потока в сечении.

Величина называется полным импульсом потока в сечении F.

Тогда силу R можно определить по формуле: , где -полный импульс потока во входном сечении канала, -в выходном канале.