лекция. Лекция 2. Потери давления в трубопроводе при турбулентном течении неустойчивых эмульсий

• Название: Потери давления в трубопроводе при турбулентном течении неустойчивых эмульсий
• Анкор: лекция
• Дата: 24.04.2023
• Размер: 2.68 Mb.
• Имя файла: Лекция 2.docx
• Тип: Лекция; #1085790

Лекция 2

ПОТЕРИ ДАВЛЕНИЯ В ТРУБОПРОВОДЕ ПРИ

ТУРБУЛЕНТНОМ ТЕЧЕНИИ НЕУСТОЙЧИВЫХ ЭМУЛЬСИЙ

Известно, что на нефтяных месторождениях страны широкое распространение получила внутритрубопроводная деэмульсация нефти, которая оказалась эффективным методом промысловой подготовки нефти, в ряде случаев полностью заменяющим подготовку ее на специальных установках

При введении деэмульгатора в турбулентный поток обводненной нефти в трубопроводе происходят интенсивное разрушение бронирующих оболочек на глобулах пластовой воды и укрупнение незащищенных глобул в десятки и сотни раз. В результате этого в трубопроводе появляется неустойчивая макроэмульсия, которая существует под действием турбулентных пульсаций одной жидкости на другую и легко расслаивается на нефть и воду при ламинарном режиме течения или в отстойных резервуарах.

Транспортировка неустойчивых эмульсий осуществляется зачастую на значительные расстояния, достигающие 100 км. При расчете трубопроводов, транспортирующих нефтяные эмульсии ,коэффициент гидравлического сопротивления определяется обычно по формуле Блазиуса с подстановкой в число Рейнольдса плотности эмульсии и ее эффективной вязкости .

Для неустойчивых грубодисперсных эмульсий такой подход не учитывает влияния глобул дисперсной фазы на интенсивность турбулентности дисперсионной среды, что приводит к существенному завышению расчетных коэффициентов гидравлического сопротивления и к росту капитальных затрат при строительстве трубопроводов .

Ранее авторами были получены расчетные формулы для определения коэффициента гидравлического сопротивления при турбулентном течении разбавленных эмульсий* в зоне гладкостенного сопротивления. При выводе этих зависимостей диаметр глобул эмульсии определяли по формуле А.Н. Колмогорова. Однако, это допущение применимо лишь в первом приближении, так как указанная формула устанавливает зависимость критического (максимального) диаметра глобул от основных параметров потока. Под разбавленной эмульсией понимается такая, в которой глобулы дисперсной фазы могут свободно перемещаться относительно друг друга и с содержанием дисперсной фазы <0,524.

Формулы для определения коэффициента гидравлического сопротивления э при турбулентном течении неустойчивых эмульсий принимают следующий вид:
(1)
Где -средняя скорость течения эмульсий в трубопороводе, _э и _с –динамическая вязкость эмульсии и дисперсионной среды, э, с, ф –плотность эмульсии, дисперсионной среды и дисперсной фазы, -межфазное натяжение, -объемная доля дисперсной фазы, D-внутренний диаметр трубы, 0- безразмерная толщина ламинарного подслоя
Динамическая вязкость неустойчивой эмульсии определяется по уравнению Бринкмана
m_э=m_с(1-b)^-2,5 (2)
На основании реологических исследований показана применимость уравнения (2) при скоростях сдвига Vc<100 /с. В реальных промысловых трубопроводах скорость сдвига не бывает выше указанного предела. В этих условиях деформация глобул дисперсной фазы незначительна и не приводит к возникновению дополнительного напряжения сдвига и проявлению неньютоновского поведения неустойчивых эмульсий .

Глобулы диспергированной жидкости оказывают влияние на турбулентную кинематическую вязкость, что проявляется в уменьшении участка смешения по сравнению с турбулентным течением однофазной жидкости. Это обусловливается прежде всего уменьшением объема, в котором происходит диссипация турбулентной энергии, поскольку пленка поверхностно-активных веществ, адсорбируемых на поверхности раздела жидкостей, препятствует проникновению пульсационных движений внутрь глобул. Кроме того, вследствие превышения размеров капелек изучаемых эмульсий внутреннего масштаба турбулентности дисперсионной среды происходит гашение турбулентных пульсаций дисперсионной среды на поверхности капелек.

ствует проникновению пульсационных движений внутрь глобул. Кроме того, вследствие превышения размеров капелек изучаемых эмульсий внутреннего масштаба турбулентности дисперсионной среды происходит гашение турбулентных пульсаций дисперсионной среды на поверхности капелек.

Влияние этих двух факторов на величину коэффициента гидравлического сопротивления растет с увеличением содержания дисперсной фазы и степени дисперсности эмульсии. В результате этого при развитом турбулентном режиме течения по трубопроводу неустойчивых эмульсий имеет место снижение удельных потерь давления при возрастании содержания дисперсной фазы, несмотря на рост коэффициента динамической вязкости эмульсии по сравнению с вязкостью нефти.

Полученные с учетом этого явления формулы Медведева В.Д., Гужова А.И., Медведева Л.П. дают существенно меньшие значения э нежели расчет по Блазиусу
l_э = 0,3164/Re_э ^0,25 (3)
который рекомендуется в некоторых работах для определения гидравлических сопротивлений при течении эмульсий в трубах.

На рис. 1 приведена зависимость удельных потерь давления от содержания дисперсной фазы. Опытные точки сопоставляются с расчетными по формулам (1 и 3). Видно, что расчет потерь давления с определением э, по Блазиусу существенно превышает опытные значения удельных потерь давления (при  = 0,40,5 расхождение достигает 45%). В то же время отклонение опытных точек от расчетной кривой с определением э по (1) не превышает ± 6%. Это позволяет рекомендовать формулы для гидравлического расчета трубопроводов, транспортирующих неустойчивые эмульсии при внутритрубной деэмульсации нефти.



Рис. 1. Зависимость удельных потерь давления от содержания дисперсной фазы

при _см равных 1,7(1) и 1,3 м/с (2)

Расчетные 3 - по формуле (1); 4 - по Блазиусу.

Компьютерное моделирование процесса расслоения эмульсии в трубопроводе

При проектировании систем нефтегазосбора с применением внутритрубной деэмульсации правильно подобранный диаметр трубопровода (в дальнейшем называемый рациональным) должен обеспечивать разрушение бронирующих оболочек и укрупнение капель до размера, при котором будет эффективно работать отстойная аппаратура. В тоже время этот диаметр должен быть таким, чтобы в трубопроводе, когда это нежелательно, не возникало расслоения потока. Формально выбор рационального диаметра трубопровода мог бы быть осуществлен с помощью диаграмм структур потока, полученных для лабораторных условий. Однако, области значений чисел Рейнольдса, Вебера и Фруда, соответствующих лабораторным и промысловым условиям, не перекрываются и перенос результатов оказывается проблематичным.

В работах [198, 200] для монодисперсных эмульсий предложен метод расчета труб из условия, что расслоение потока возникает в тех случаях, когда скорость седиментации капель оказывается равной или выше среднеквадратичной пульсационной скорости. Метод дает приемлемые значения диаметра трубопровода и применяется на нефтяных промыслах, где подготовка продукции скважин ведется по совмещенной технологии с использованием трубной деэмульсации. Однако этот метод не учитывает полидисперсности и степени обводненности эмульсии. Кроме того, как это будет показано, даже статические условия возникновения расслоения эмульсии не совсем верно отвечают реальной динамической картине формирования структуры потока, в том числе перехода его из эмульсионного в расслоенное состояние. Метод отражает картину только предельных состояний, исключая промежуточные: движение в трубе жидкости в виде эмульсии или же полностью расслоенного потока. В дальнейшем метод был модифицирован в работе [200], где концентрация дисперсной фазы была учтена косвенным образом через коэффициент гидравлического сопротивления. Поскольку допущения и основа метода расчета остались неизменными, то результаты и в этом случае остаются не адекватны реальным.

В работе изложены результаты компьютерного моделирования процесса расслоения в трубопроводе. Для этого была построена динамическая модель движения эмульсии, которая с учетом полидисперсности описывает изменение распределения капель дисперсной фазы но размерам (РКР), обусловленное процессами турбулентной диффузии и седиментации. Процессы дробления и коалесценции учтены путем задания исходного эмпирического РКР.

Модель седиментационно-турбулентного равновесия. Диффузионные процессы являются выравнивающими. Гравитационный эффект относится к разделяющим. Совместное действие столь противоположных по конечному результату механизмов приводит к известному явлению изменения числа частиц в объеме по высоте.

Для количественного описания явления целесообразно использовать методологию работы , разработанную для коллоидных систем.

Согласно первому закону Фика, диффузионный поток частиц дисперсной фазы, принадлежащих к i-й фракции (интервал размеров i и i-1), определяется по формуле (1):


где: D_Т- коэффициент турбулентной диффузии; n- число частиц i-й фракции в единице объема; у - ось, направленная вверх для случая более тяжелой дисперсной фазы и вниз, если она легче сплошной фазы.

Тогда седиментационный поток частиц может быть отражен выражением (2):


где: v _i - скорость седиментации частиц i-й фракции.

Условие динамического равновесия наступает тогда, когда J d i =JsiЭто позволяет придти к обыкновенному дифференциальному уравнению первого порядка (3)


Предполагая в 1-м приближении, что величины vi, Diне зависят от у, после интегрирования получим следующее выражение для численной концентрации i-й фракции (4):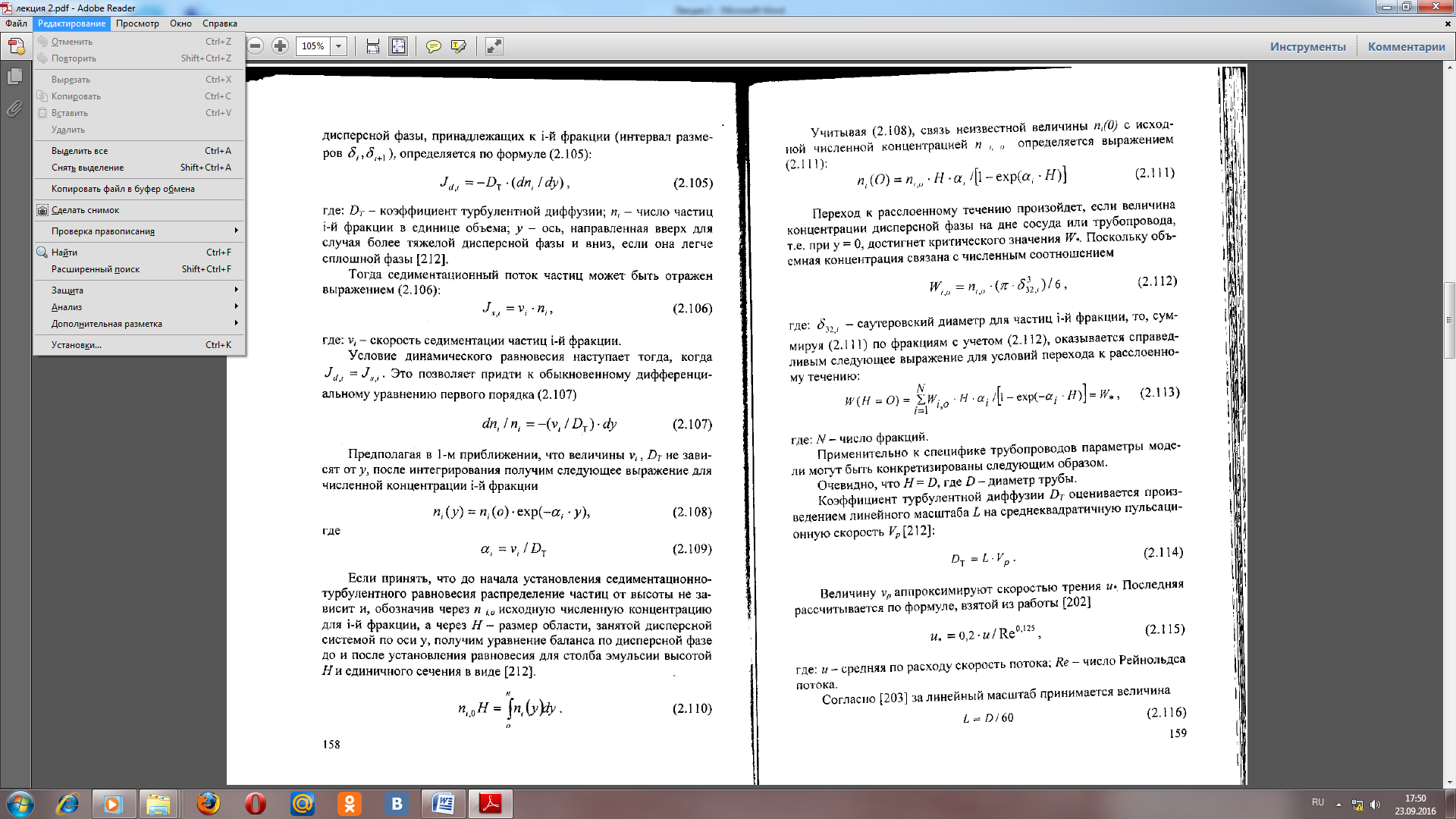


Если принять, что до начала установления седиментационно-турбулентного равновесия распределение частиц от высоты не зависит и, обозначив через ni исходную численную концентрацию для i-й фракции, а через Н - размер области, занятой дисперсной системой по оси у, получим уравнение баланса по дисперсной фазе до и после установления равновесия для столба эмульсии высотой Н и единичного сечения в виде [5].

Учитывая (4), связь неизвестной величины пi (0) с исходной численной концентрацией ni определяется выражением (6)


Переход к расслоенному течению произойдет, если величина концентрации дисперсной фазы на дне сосуда или трубопровода, т.е. при у = 0, достигнет критического значения W*. Поскольку объемная концентрация связана с численным соотношением (7)


где: ₃₂i - саутеровский диаметр для частиц i-й фракции, то, суммируя (6) по фракциям с учетом (7), оказывается справедливым следующее выражение для условий перехода к расслоенному течению (8):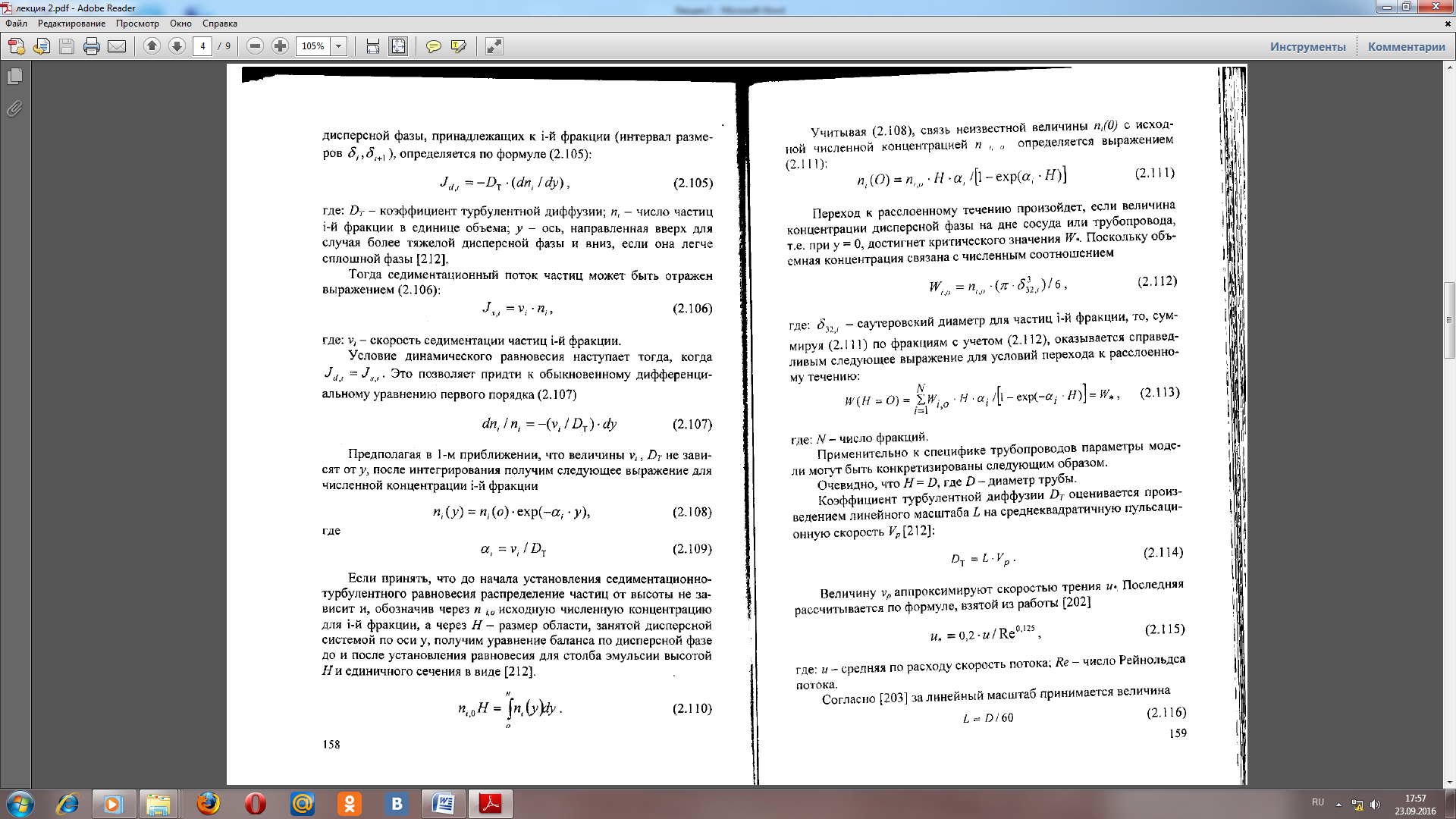


где: N - число фракций.

Применительно к специфике трубопроводов параметры модели могут быть конкретизированы следующим образом.

Очевидно, что Н= D, где D - диаметр трубы.

Коэффициент турбулентной диффузии D_Tоценивается произведением линейного масштаба L на среднеквадратичную пульсационную скорость Vp(9):

D_T = LVp

Величину vp аппроксимируют скоростью трения и .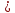


где: и - средняя по расходу скорость потока; Re - число Рейнольдса потока.

За линейный масштаб принимается величина L = D/60

Скорость седиментации определяется по формуле Стокса (11)



где:  - разность плотностей фаз;  - динамическая вязкость сплошной фазы
Величины ni,32i, Wi характеризующие i-ю фракцию, находят следующим образом. Пусть

Р₀ (х) есть плотность распределения объема дисперсной фазы по диаметрам частиц, т.е.

Р₀ (x)dx -это объем, заключенный в частицах диаметром от х до х +dx. Тогда имеем (12):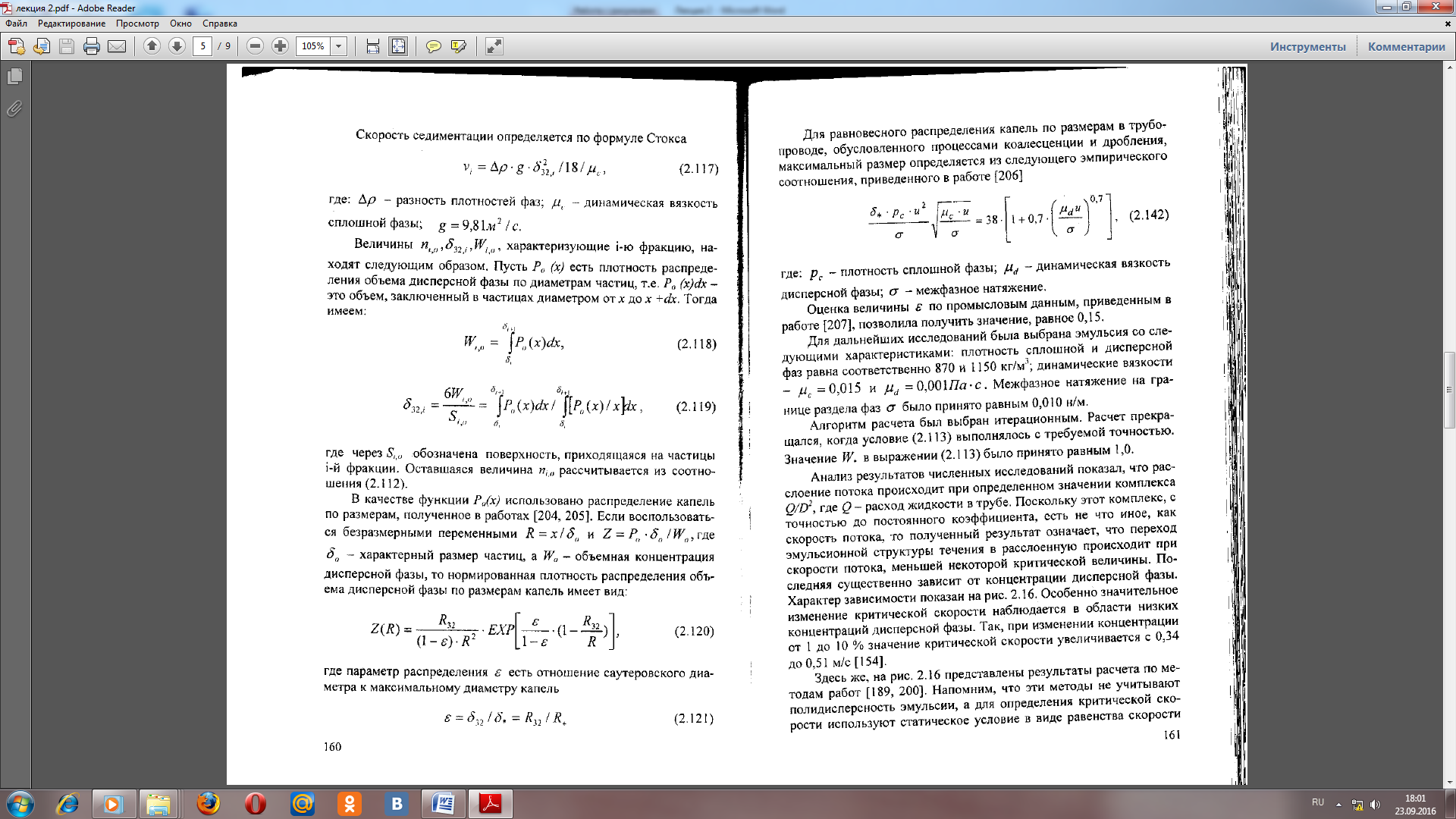

где через S_i0обозначена поверхность, приходящаяся на частицы i-й фракции. Оставшаяся величина рассчитывается из соотношения (7).

В качестве функции Р0(х) использовано распределение капель по размерам. Если воспользоваться безразмерными переменными R = x/₀и Z =P₀₀/W₀, где₀ - характерный размер частиц, a W₀- объемная концентрация дисперсной фазы, то нормированная плотность распределения объема дисперсной фазы по размерам капель имеет вид (13):



где параметр распределения  есть отношение саутеровского диаметра к максимальному диаметру капель (14):


Для равновесного распределения капель по размерам в трубопроводе, обусловленного процессами коалесценции и дробления, максимальный размер определяется из следующего эмпирического соотношения:

с-плотность сплошной фазы; - динамическая вязкость дисперсной фазы;  - межфазное натяжение.

Оценка величины  по промысловым данным позволила получить значение, равное 0,15.

Для дальнейших исследований была выбрана эмульсия со следующими характеристиками: плотность сплошной и дисперсной фаз равна соответственно 870 и 1150 кг/м3; динамические вязкости 0,015 и 0,00 мПас. Межфазное натяжение на границе раздела фаз было принято равным 0,010 н/м.

Алгоритм расчета был выбран итерационным. Расчет прекращался, когда условие (8) выполнялось с требуемой точностью. Значение W, в выражении (8) было принято равным 1,0.

Анализ результатов численных исследований показал, что расслоение потока происходит при определенном значении комплекса Q/D², где Q - расход жидкости в трубе.

Поскольку этот комплекс, с точностью до постоянного коэффициента, есть не что иное, как скорость потока, то полученный результат означает, что переход эмульсионной структуры течения в расслоенную происходит при скорости потока, меньшей некоторой критической величины. Последняя существенно зависит от концентрации дисперсной фазы.

Характер зависимости показан на рис. 1. Особенно значительное изменение критической скорости наблюдается в области низких концентраций дисперсной фазы. Так, при изменении концентрации от 1 до 10 % значение критической скорости увеличивается с 0,34 до 0,51 м/с .

Здесь же, на рис. 1 представлены результаты расчета по методам работ [189, 200]. Напомним, что эти методы не учитывают полидисперсность эмульсии, а для определения критической скорости используют статическое условие в виде равенства скорости седиментации капель среднеквадратичной скорости турбулентных пульсаций.



Рис. 1. Зависимость критической скорости потока и_оот концентрации дисперсной фазы W₀ в

объемных единицах
Динамическая модель с учетом полидисперсности позволяет раскрыть влияние на переход от одной структуры потока к другой таких важных параметров, как концентрация дисперсной фазы и ее распределение по размерам капель.

Для выбора рационального диаметра трубопровода необходимо задать обводненность эмульсии и из рис. 1 найти значение критической скорости. Диаметр трубопровода рассчитывается из известного соотношения между расходом Q и скоростью течения:


Рассмотрим вопрос о размере капель, соответствующем переходу течения из эмульсионной структуры в расслоенное.

Пусть деэмульгатор не подается в систему сбора. В этом случае имеем стабильную эмульсию, и процессами коалесценции капель на линейных участках трубопроводов можно пренебречь. Расход жидкости считаем постоянным и равным 31,7 кг/с, варьируются только диаметр трубопровода и обводнённость. Полученные результаты представлены на рис. 2 в виде корреляционной связи между размером капель и диаметром трубопровода (см. рис. 2 а); размером капель и величиной обводненности эмульсии (см. рис. 2 б). Линии 2-4 и 6 на рис. 3а соответствуют значениям обводненности 40, 10, 1 и 0,1 объемных процента.

Линии 1-7 на рис. 3 б соответствуют значениям диаметра трубопровода 0,10; 0,15; 0,20; 0,25; 0,30; 0,35; 0,40.



Рис. 3 а. Корреляционная связь между диаметром трубопровода и глобул воды (Q = 31,7 кг/с)

Кривые 5, 3, 1 - зависимость максимального диаметра капель, способных витать в потоке, от диаметра трубопровода при обводненности эмульсии, равной 0,1; 1; 10 и 40%; кривая 4 - т о же, но в рамках старой теории; кривая 6 - зависимость максимального диаметра капель, устойчивых к дроблению, от диаметра трубопровода (по Слейчеру): кривая 7 - пересчет кривой 6 на саутеровский диаметр.



Рис. 3 б. Корреляционная связь между обводненностью эмульсии и диаметром глобул

Кривые 1-7 - для диаметра трубы, равного 0,10; 0,15; 0,20; 0,25; 0,30;0,35, 0,40 м.

Из рис. 3 следует, что в логарифмических переменных связи имеют линейный характер и справедлива формула (15)


где А, В, С-постоянные.

При А = -1 и В = -0,5 формула приводится к виду (16)



Для обводненности не выше 10% оценка константы С дала величину 31,2 ±1,5 мм2. При более высокой обводненности данные отклоняются от линейного закона (рис. 3 б ) и для 40% эмульсии С=26,0±1,0 мм2.

В случае, когда деэмульгатор подается в систему нефтегазосбора, на линейных участках трубопроводов бронирующие оболочки капель разрушаются и эмульсия становится нестабильной. В конце концов процессы коалесценции и дробления капель приводят к установлению динамического равновесия.

В этом случае задача состоит в определении наибольшего размера капель (саутеровского диаметра), при котором поток еще не будет расслаиваться. Процессы коалесценции и дробления учитываются с использованием уравнения (13).

Необходимо более подробно рассмотреть специфику принятой методологии оценки возможности расслоения потока в трубопроводах. Имеется достаточное число публикаций по этому вопросу, принципиально мало отличающихся друг от друга. Как правило, осуществляются лабораторные исследования, по которым в результате обработки получают формулы. Отдельные работы поднимаются до уровня определения критериальных чисел. Однако это мало что дает в практическом плане. Перенос таких лабораторных данных на промысловые условия не совсем корректен. В лучшем случае речь может идти о достижении частичного подобия лабораторных условий реальным промысловым. И практика подтверждает это: обилие различных формул, хорошо описывающих те опытные данные, на которых они были получены, мало пригодны за их пределами.

Рассмотрим методологию определения критической скорости, лежащей в основе большинства работ. Её можно изложить так: есть капля; под действием силы Архимеда она движется в окружающей среде (если легче, то всплывает; когда тяжелее среды – то оседает); скорость ее движения зависит от режима - для не очень крупных капель режим ламинарный и можно пользоваться известной формулой Стокса; кроме гравитационного движения капля участвует в пульсационном движении среды; капля не способна осесть и оказывается взвешенной в потоке, если среднеквадратичная скорость турбулентных пульсаций выше скорости ее осаждения; для определения критической скорости потока приравнивают указанные скорости. В конечном итоге получают связь между размером капель, способных витать в потоке, и скоростью потока.

Внешне методология логична. Тем не менее, она дает размеры капель, способных витать в потоке, намного превышающие реально наблюдаемые. Соответственно, она завышает значение критической скорости. скорости.

Более правилен другой подход к решению этой задачи по следующей схеме:

- эмульсия рассматривается не как «одиночная капля - окружающая среда», а как дисперсная система, причем не моно-, а поли-;

- замена статического условия равновесия динамическим;

- применение имитационного моделирования, рассчитывая на компьютере варианты развития системы во времени и пространстве.

В такой методологии первый пункт уже раскрыт на примере рассмотренной задачи укрупнения капель. Последний пункт реализуется по нижеследующей схеме: сечение трубопровода разделяется горизонтальными плоскостями от нижней образующей (дно трубы) до верхней на несколько слоев. Их число должно быть достаточно большим, но не настолько, чтобы нарушалось понятие физически малого (элементарного) объема. Под последним имеется ввиду то, что понимал Ландау, с той лишь разницей, что роль молекул в нашей схеме выполняют капли. Для каждого слоя составляется уравнение баланса числа капель. Смысл его состоит в том, что, если известно число капель в слоях в какой-то момент времени, то за малое приращение времени произойдет фиксируемое изменение числа капель в каждом из слоев в связи с поступлением в него капель, осаждающихся из вышележащего слоя и ухода капель по той же причине в нижележащий слой. Кроме того, на границе слоев, имеющих различную концентрацию капель, будут существовать диффузионные потоки. Поэтому в уравнение баланса войдут члены, описывающие изменение числа капель в слое за счет диффузионного обмена с соседними слоями. Шаг за шагом во времени или, что эквивалентно, по длине трубопровода, прослеживается изменение профиля концентрации по высоте трубы. По достижению определенного времени, соответствующей некоторой длине трубопровода, профиль перестает меняться. Устанавливается динамическое равновесие - на каждом уровне по высоте трубы число оседающих капель оказывается равным числу капель, выносимых диффузионными токами.

Что касается второго пункта этой методологии, то очевидно, что расслоение возникает тогда, когда объемная концентрация воды на нижнем уровне трубопровода достигает критического значения при отсутствии на глобулах бронирующих оболочек. Минимальная скорость потока, при которой это может произойти, и принимается за критическую скорость.

Результаты компьютерного моделирования движения девонской эмульсии по трубопроводу показали, что в начале трубопровода капли воды распределены равномерно, т.е. эмульсия однородна по сечению трубопровода.

Во всех случаях обводненность нефти изменялась в широких пределах. Первый вариант моделировал группу скважин, подключенных к общему трубопроводу. Расход жидкости при этом изменялся за счет числа работающих скважин или в связи с изменением дебитов некоторых из них. Второй вариант связан с решением задач предварительного сброса воды с помощью КДФ в местах, максимально приближенных к объектам закачки воды в продуктивные пласты.

Анализ результатов расчетов показал, что для возникновения эффекта расслоения потока важно не только значение расхода Q или диаметра трубы D, а значение комплекса Q/D/D в целом. В обоих вариантах имело место расслоение потока, если значение комплекса было меньше определенной величины, зависящей от обводненности нефти. Поскольку комплекс с точностью до постоянного значения коэффициента есть не что иное, как скорость потока, то тем самым правомерно признать существование критической скорости. Причем, последняя существенно зависит от обводненности нефти. Характер зависимости представлен на рис. 2 (кривая 2). Особенно существенное изменение критической скорости имеет место в области низких значений обводненности. Так, при изменении обводненности от 1 до 10% значение критической скорости увеличивается с 0,34 до 0,51 м/с.

Для сравнения на рис. 4 приведены данные, полученные по разным методам (прямая 1) и (кривая 3).


Рис. 4. Нормированная плотность распределения объема дисперсной фазы W по диаметрам капель d: 0 – исходное распределение; 1,2,3 -соответственно в нижней, средней и верхней части трубопровода.

Известные методы не учитывают обводненность эмульсии, зато принимают в расчет разрушенность бронирующих оболочек на глобулах воды.

Практическая ценность кривой 2 (рис. 4) связана с возможностью по заданной обводненности найти значение скорости, при которой наступает расслоение потока с разрушенными бронирующими оболочками на глобулах воды. Это позволяет рассчитать необходимый диаметр трубопровода, пользуясь при этом известным соотношением между расходом жидкости и скоростью течения потока.

Полидисперсная модель дает возможность получить информацию об изменении по сечению потока распределения капель по размерам. Расчеты, выполненные для 10 % эмульсии при диаметре трубы 0,3 м, показали, что в условиях перехода от эмульсионной к расслоенной структуре потока (Q = 32,8 кг/с) наблюдается концентрация крупных капель в тонком слое нижней части трубы. Характер изменения нормированной плотности распределения объема дисперсной фазы по диаметрам капель для различных уровней по высоте потока показан на рис. 4. Для слоя толщиной 1,6 см в нижней части трубы объем дисперсной фазы распределен по фракциям почти равномерно (кривая 1). Для средней части трубы и выше (кривые 2 и 3) происходит обеднение эмульсии каплями крупных размеров. Распределения характеризуются острым максимумом, несколько смешенным в область малых размеров по сравнению с исходным распределением.