зачет по геометрии 7 класс. Билеты 7 класс. Билеты 7 класс билет 1

• Название: Билеты 7 класс билет 1
• Анкор: зачет по геометрии 7 класс
• Дата: 26.04.2022
• Размер: 206.5 Kb.
• Имя файла: Билеты 7 класс.doc
• Тип: Задача; #498537

БИЛЕТЫ 7 КЛАСС

Билет №1.

1. 
   Определение биссектрисы треугольника. Замечательное свойство биссектрисы треугольника.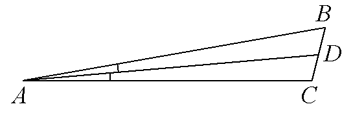
   
2. 
   Признак равенства прямоугольных треугольников по гипотенузе и катету (доказательство).
   
3. 
   1) В треугольнике ABC AD — биссектриса, угол C равен 104°, угол CAD равен 5°. Найдите угол B. Ответ дайте в градусах.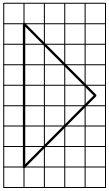
   

2) На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его биссектрисы, выходящей из вершины прямого угла.

4. 
   Точка D на сто­ро­не AB тре­уголь­ни­ка ABC вы­бра­на так, что AD = AC. Известно, что ∠CAB = 80° и ∠ACB=59∘. Най­ди­те угол DCB. Ответ дайте в градусах.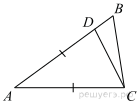
   
5. 
   Задача из дополнительного банка заданий
   

Билет №2.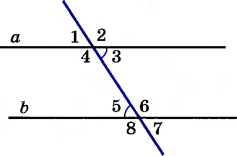

1. 
   Определение медианы треугольника. Замечательное свойство медианы треугольника.
   
2. 
   Теорема о внешнем угле треугольника (доказательство).
   
3. 
   1) Дано: a||b, 5 = 60⁰. Найдите 1.
   

2) На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.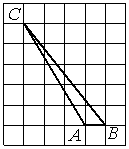

4. 
   В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах.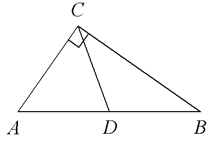
   
5. 
   Задача из дополнительного банка заданий
   

Билет №3.

1. 
   Определение высоты треугольника. Замечательное свойство высоты треугольника.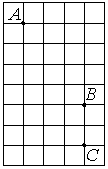
   
2. 
   Признак равенства прямоугольных треугольников по гипотенузе и острому углу (доказательство).
   
3. 
   1) Дан равносторонний треугольник АВС. Найдите величину внешнего угла при вершине С.
   

2) На клетчатой бумаге с размером клетки 1×1 отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC.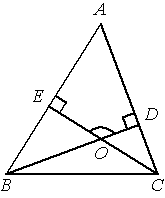

4. 
   В треугольнике ABC угол A равен 56°, углы B и C – острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.
   
5. 
   Задача из дополнительного банка заданий
   

Билет №4.

1. 
   Определение равнобедренного треугольника. Свойства равнобедренного треугольника.
   
2. 
   Теорема о сумме двух острых углов прямоугольного треугольника (доказательство).
   
3. 
   1) Луч OF – биссектриса угла AOB, AOB=62⁰. Найдите AOF.
   

2) На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.

4. 
   В остроугольном треугольнике ABC угол A равен 78°, BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
   
5. 
   Задача из дополнительного банка заданий
   

Билет №5.

1. 
   Определение равностороннего треугольника. Свойство равностороннего треугольника.
   
2. 
   Сформулируйте и докажите признак параллельности двух прямых по внутренним односторонним углам.
   
3. 
   1) В треугольнике АВСАМ является медианой. Найдите величину отрезкаМС,
   

еслиВС = 21 см.

2) В треугольнике ABC AD — биссектриса, угол C равен 62°, угол CAD равен 32°. Найдите угол B. Ответ дайте в градусах.

4. В треугольнике ABC угол C равен 58°, биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах.

5. Задача из дополнительного банка заданий

Билет №6.

1. 
   Определение окружности, радиуса, диаметра, хорды.
   
2. 
   Теорема о свойстве биссектрисы равнобедренного треугольника (доказательство).
   
3. 
   1) Луч ОС делит угол АОВ на два угла. Найдите угол ВОС, если угол АОВ равен 78⁰, а угол АОС на 18⁰ меньше угла ВОС.
   

2) Найдите угол N.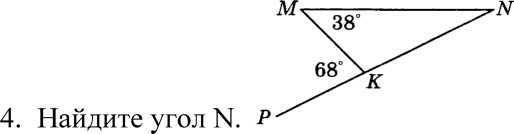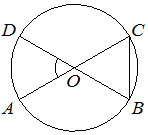

4. 
   Отрезки AC и BD — диаметры окружности  с центром O. Угол ACB равен 56°. Найдите  угол AOD. Ответ дайте в градусах.
   
5. 
   Задача из дополнительного банка заданий
   

Билет №7.

1. 
   Определение параллельных прямых, параллельных отрезков. Свойство параллельных прямых.
   
2. 
   Теорема о сумме внутренних углов треугольника (доказательство).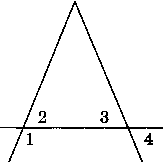
   
3. 
   1) Найдите смежные углы, если один из них на 74⁰ больше другого.
   

2) На рисунке 1=48⁰, 2=3. Найдите 4.

4. 
   Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.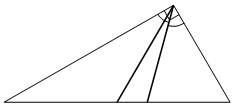
   
5. 
   Задача из дополнительного банка заданий
   

Билет №8.

1. 
   Определение внешнего угла треугольника.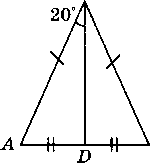
   
2. 
   Свойство углов равнобедренного треугольника (доказательство).
   
3. 
   1) В равнобедренном треугольнике основание в три раза меньше боковой стороны, а периметр равен 49 см. Найдите стороны треугольника.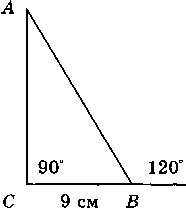
   

2) Найдите угол А.

4. 
   Найдите длину гипотенузы треугольника АВС.
   
5. 
   Задача из дополнительного банка заданий
   

Билет №9.

1. 
   Сформулируйте признаки равенства треугольников.
   
2. 
   Теорема о сумме двух острых углов прямоугольного треугольника (доказательство).
   
3. 
   1) В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине В равен 150⁰. Найдите углы при основании треугольника.
   

2) Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см больше другой. Найдите стороны треугольника.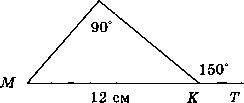

4. 
   Найдите длину катета МР треугольника МРК.
   
5. 
   Задача из дополнительного банка заданий
   

Билет №10.

1. 
   Определение прямоугольного треугольника. Стороны и углы прямоугольного треугольника.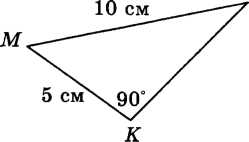
   
2. 
   Теорема о вертикальных углах (доказательство)
   
3. 
   1) В треугольнике АВС А=80⁰, В=60⁰. Чему равен С?
   

2. 
   Найдите острые углы треугольника MNK.
   

4. 
   Острые углы прямоугольного треугольника равны 84° и 6°. Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.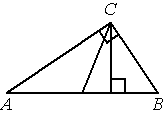
   
5. 
   Задача из дополнительного банка заданий
   

Билет №11.

1. 
   Определение расстояния от точки до прямой.
   
2. 
   Доказать, что если прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую.
   
3. 
   1) Точка Р делит отрезок MN на два отрезка. MN равен 12 см, NP равен 9 см. Найдите отрезок MP.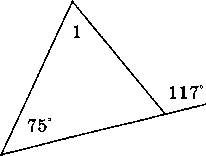
   

2. 
   Найдите угол 1.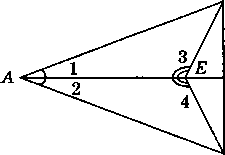
   

4. 
   Дано: 1=2, 3=4. Доказать: BD=CD.
   
5. 
   Задача из дополнительного банка заданий
   

Билет №12.

1. 
   Виды треугольников. Определение каждого вида треугольника. Неравенство треугольника.
   
2. 
   Признак равенства прямоугольных треугольников по катету и острому углу (доказательство).
   
3. 
   1) В прямоугольном треугольнике АВС (А - прямой), В=60⁰. Найдите величину угла С.
   

2) На рисунке 1=102⁰, 2=3. Найдите 4.

4. 
   В равнобедренном треугольнике MNK с основанием MK длина его медианы NP равна 6 см. Периметр треугольника MNP равен 24 см. Найдите периметр треугольника MNK.
   
5. 
   Задача из дополнительного банка заданий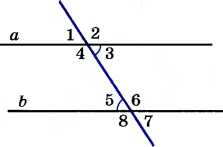
   

Билет №13.

1. 
   Секущая. Виды углов при пересечении двух параллельных прямых третьей.
   
2. 
   Теорема о свойстве смежных углов (доказательство).
   
3. 
   1) Дано: a||b, 6 = 120⁰. Найдите 4.
   

2) В треугольнике ABC угол C равен 133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.

4. 
   В равнобедренном треугольнике АВС В=104⁰. АD– высота этого треугольника. Найдите угол DAC.
   
5. 
   Задача из дополнительного банка заданий
   

Билет №14.

1. 
   Определение вертикальных углов.
   
2. 
   Сформулируйте и докажите признак параллельности двух прямых по соответственным углам.
   
3. 
   1) Отрезки АС и ВD при пересечении точкой О делятся пополам. Докажите, что треугольник AOB равен треугольнику DOC.
   

2. 
   Найдите величину угла С.
   

4. 
   В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=26, BC=18. Найдите CM.
   
5. 
   Задача из дополнительного банка заданий
   

Билет №15.

1. 
   Определение перпендикулярных прямых.
   
2. 
   Сформулируйте и докажите свойство катета прямоугольного треугольника, лежащего против угла в 30⁰.
   
3. 
   1) В треугольнике ABC известно, что AB=BC, ∠ABC=106°. Найдите угол BCA. Ответ дайте 
   в градусах.
   

2) В равнобедренном треугольнике основание в три раза больше боковой стороны, а периметр равен 60 см. Найдите стороны треугольника.

4. 
   На рисунке АВЕ=104⁰, АСВ=76⁰, АС=12 см. Найдите сторону АВ треугольника АВС.
   

5. 
   
   
   
   Задача из дополнительного банка заданий
   

Задачи по геометрии за курс 7 класса.

1. 
   На прямой a расположены точки A, B, C, причем A B = 5см, BC = 7 см. Какой может быть длина отрезка AC.
   
2. 
   Прямой угол ADB разделен лучом DC на два угла, причем один угол на 9⁰ больше другого. Найдите градусные меры этих углов.
   
3. 
   Угол AOB, равный 124⁰, лучом OC разделен на два угла, разность которых равна 34⁰. Найдите эти углы. Чему равен угол, образованный лучом OC и биссектрисой угла AOB.
   
4. 
   Угол AOB, равный 136⁰, лучом OC разделен на два угла, градусные меры которых относятся как 3:1. Найдите эти углы. Чему равен угол, образованный лучом OC и биссектрисой угла AOB.
   
5. 
   Луч BM делит развернутый угол ABC в отношении 5:1, считая от луча BA. Найдите угол ABK, если BK – биссектриса угла MBC.
   
6. 
   Один из смежных углов на 50⁰ больше другого. Найдите эти углы.
   
7. 
   Разность двух смежных углов равна 54⁰. Найдите эти углы.
   
8. 
   Прямая ВК перпендикулярна прямым МВ и КТ. Докажите, что треугольники МВО и ОКТ равны. Найдите углы ОМВ, ВОМ, ОТК, если известно, что МВ=КТ, а угол ТОК=40⁰. (Обязательно доказательство равенства треугольников)
   

9. 
   Отрезки АС и ВD пересекаются в точке О. ВD = АС, ОВ=ОС. а) Докажите, что ∆ АОВ = ∆ СОD;
   

б) Найдите периметр ∆ СОD, если АВ=9см, ВО=5см, ОD=7см.

10. 
    В ∆АВС АВ = ВС, ВЕ – медиана треугольника АВС, Угол АВЕ =41˚. Найдите углы АВС и СЕВ.
    
11. 
    Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма трех из них равна 307⁰.
    
12. 
    На медиане CM равнобедренного треугольника ABC с основанием AB взята точка О.Докажите, что треугольник AOB равнобедренный.
    
13. 
    Один из внешних углов равнобедренного треугольника равен 126˚. Найдите углы треугольника.
    
14. 
    AD и CE – биссектрисы равнобедренного треугольника с основанием AC. Докажите, что AEC = CDA.
    
15. 
    Точки C и D расположены по разные стороны от прямой AB так, что AD = AC, BD = DC. Докажите, что AB – биссектриса угла DAC.
    
16. 
    Определите углы: МРО, РВО, ОВТ, ХКО, АКО, КОА, ОАК, ОАС, ВОА, РОК, если известно, что угол ОРВ=52⁰, а угол РОВ=102⁰, РВ параллельно АК.
    

17. 
    Найдите все углы, образованные при пересечении двух параллельных прямых f и d секущей c, если один из углов на 50˚ больше другого.
    
18. 
    В треугольнике АВС <А=40˚,<В=70˚. Через вершину В проведена прямая ВD так, что луч ВС – биссектриса угла АВD. Докажите , что АС и ВD параллельны.
    
19. 
    В треугольнике ABC угол A равен 70⁰, внешний угол при вершине B равен 79⁰. Найдите угол C. Ответ дайте в градусах.
    
20. 
    В треугольнике ABC угол A равен 39⁰, АС=ВС. Найдите угол C. Ответ дайте в градусах.
    
21. 
    В треугольнике ABC угол C равен 130⁰,АС=ВС. Найдите угол A. Ответ дайте в градусах.
    
22. 
    В треугольнике ABC АС=ВС. Внешний угол при вершине B равен 152⁰. Найдите угол C. Ответ дайте в градусах.
    
23. 
    Сумма двух углов треугольника и внешнего угла к третьему равна 120⁰. Найдите этот третий угол. Ответ дайте в градусах.
    
24. 
    В треугольнике ABC угол C равен 90⁰, CH — высота, угол A равен 6⁰. Найдите угол BCH. Ответ дайте в градусах.
    
25. 
    Один острый угол прямоугольного треугольника на 42⁰ больше другого. Найдите больший острый угол. Ответ дайте в градусах
    
26. 
    Дан прямоугольный треугольник АВС с прямым углом С. Угол В равен 30⁰. Гипотенуза равна 12, а катет СВ равен 10. Определите периметр треугольника и угол А.
    
27. 
    В треугольнике АВС угол А больше угла В в 9 раз, а угол С меньше угла А на 10⁰. Определите углы треугольника и укажите, каким этот треугольник является.
    
28. 
    Угол при основании равнобедренного треугольника равен 70⁰, чему равен внешний угол при при основании треугольника, не смежный с данным углом?
    
29. 
    Внешний угол при основании равнобедренного треугольника на 20⁰ больше одного из углов при основании треугольника. Найдите углы треугольника.
    
30. 
    В треугольнике ABC точка D лежит на стороне BC, причем AD = DC.Сумма внешних углов при вершине A равна 160⁰. Найдите угол C, если AD – биссектриса угла BAC.
    
31. 
    Один из углов прямоугольного треугольника равен 30˚, а сумма гипотенузы и меньшего катета равна 12,6 см. Найдите длину гипотенузы.
    
32. 
    Дан квадрат со стороной 16 см. Точка М лежит на стороне и делит эту сторону в отношении 3:5 от вершины . Прямая, проходящая через точку М пересекает сторону в точке Т, таким образом, что угол ВТМ равен 120⁰. Из вершины к прямой ТМ проведен перпендикуляр . Определите длину этого перпендикуляра.
    
33. 
    Один из внешних углов прямоугольного треугольника равен 120⁰. Найдите большую и меньшую стороны треугольника, если их сумма равна 18 см.
    
34. 
    В прямоугольном треугольнике ABC с гипотенузой BC и углом B равным 60⁰, проведена высота AD. Найдите DC, если DB = 2 см.
    
35. 
    В прямоугольном треугольнике ABC с гипотенузой AC, равной 12 см проведена высота BD. Найдите CD, DA если < A = 30⁰.
    

36. 
    Даны две параллельные прямые и секущая, которая пересекает прямые в точках А и В. Биссектрисы углов А и В пересекаются в точке О. Найдите периметр треугольника АВО, если известно, что АВ равно 8, угол ВАО в 2 раза меньше угла ОВА, а АК равно 12,6 см, где точка К – точка пересечения прямой АО и одной из параллельных прямых.
    

Критерии оценивания муниципального публичного зачета в 7 классе

1. 
   вопрос: 0-1 балл
   
2. 
   вопрос: 0-2 балла
   
3. 
   вопрос: 0-1 балл
   
4. 
   вопрос: 0-2 балла
   
5. 
   вопрос: 2 балла
   

• 
  Ответ на задание №1 предполагает связный рассказ
  
• 
  За ответ на вопрос №2 выставляется 2 балла, если сформулирована правильно теорема и представлено её доказательство; 1 балл, если сформулирована правильно теорема без доказательства, и 0 баллов во всех других случаях.
  
• 
  При выполнении задания №3 обучающиеся выбирают 1 задачу из двух предложенных.
  
• 
  Ответ на вопрос №4 (задача), оцениваемый двумя баллами, считается выполненным верно, если выбран правильный путь решения, понятен путь рассуждения, дан верный ответ. Если допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то выставляется на 1 балл меньше.
  
• 
  Для выполнения задания №5 предполагается выбор обучающимися задачи из дополнительного банка заданий и адресуется для обучающихся, претендующих на оценку «5». 2 балла ставится при полном верном решении.
  

Максимальное количество баллов - 6 баллов.

Шкала перевода баллов в школьную отметку муниципального публичного зачета

Отметка	пересдача	«3»	«4»	«5»
Балл	0-2	3-4	5-6	7-8