|
|
Билеты для зачета по геометрии 8 класс. билеты по геометрии 8 класс. Билеты к зачету по геометрии Итоги главы 1 (к учебнику Мерзляк А. Г. 8 класс)
Билеты к зачету по геометрии: Итоги главы 1 (к учебнику Мерзляк А.Г. 8 класс).
Билет №1.
1. Определение параллелограмма.
2. Сумма углов четырехугольника.
3. Доказать свойство средней линии трапеции.
4. Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.
|
Билет №2.
1. Определение квадрата.
2. Свойство средней линии трапеции.
3. Доказать особое свойство прямоугольника.
4. Докажите, что угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма.
|
Билет №3.
1. Высота параллелограмма.
2. Свойства прямоугольника (все).
3. Доказать один из признаков ромба.
4. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.
|
Билет №4.
1. Определение средней линии треугольника.
2. Признаки параллелограмма.
3. Доказать особое свойство ромба.
4. Докажите, что в равнобокой трапеции углы при каждом основании равны.
|
Билет №5.
1. Определение прямоугольника.
2. Свойства ромба (все).
3. Доказать свойства параллелограмма (2 св-ва).
4. Отрезок АВ – хорда окружности с центром О. Через точку А проведена касательная MN. Докажите, что 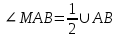 и и 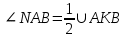 . .
|
Билет №6.
1. Определение трапеции.
2. Признаки прямоугольника.
3. Доказать один из признаков параллелограмма.
4. Докажите, что угол между высотами параллелограмма, проведенными из вершины острого угла, равен тупому углу параллелограмма.
|
Билет №7.
1. Определение ромба.
2. Свойство средней линии треугольника.
3. Доказать один из признаков прямоугольника.
4. Докажите, что длина любой стороны четырехугольника меньше суммы длин трех остальных его сторон.
|
Билет №8.
1. Определение высоты трапеции.
2. Признаки ромба.
3. Доказать свойство средней линии треугольника.
4. Диагонали равнобокой трапеции ABCD (AB=CD), пересекаются в точке О. Докажите, что AO=OD и BO=OC.
|
Билет №9.
1. Определение средней линии трапеции.
2. Свойства параллелограмма.
3. Доказать особое свойство ромба.
4. Докажите, если две дуги окружности равны, то равны и хорды, их стягивающие.
|
Билет №10.
1. Определение параллелограмма.
2. Сумма углов четырехугольника.
3. Доказать свойство средней линии трапеции.
4. Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.
|
Билеты к зачету по геометрии: Итоги главы 2 (к учебнику Мерзляк А.Г. 8 класс).
Билет №1.
1. Теорема Фалеса.
2. Третий признак подобия треугольников.
3. Свойство медиан треугольника.
4. Докажите, что средняя линия трапеции делит ее диагональ пополам.
|
Билет №2.
1. Подобные треугольники.
2. Второй признак подобия треугольников.
3. Свойство биссектрисы треугольника.
4. Докажите, что отношение периметров подобных треугольников равно коэффициенту подобия.
|
Билет №3.
1. Теорема о пропорциональных отрезках.
2. Первый признак подобия треугольников.
3. Свойство пересекающихся хорд.
4. Докажите, что в подобных треугольниках биссектрисы, проведенные из вершин соответственных углов, относятся как соответственные стороны.
|
Билет №4.
1. Лемма о подобных треугольниках.
2. Теорема Птолемея.
3. Свойство касательной и секущей.
4. Докажите, что в подобных треугольниках высоты, проведенные из вершин соответственных углов, относятся как соответственные стороны.
|
Билет №5.
1. Теорема Фалеса.
2. Третий признак подобия треугольников.
3. Свойство медиан треугольника.
4. Докажите, что средняя линия трапеции делит ее диагональ пополам.
|
Билет №6.
1. Подобные треугольники.
2. Второй признак подобия треугольников.
3. Свойство биссектрисы треугольника.
4. Докажите, что отношение периметров подобных треугольников равно коэффициенту подобия.
|
Билет №7.
1. Теорема о пропорциональных отрезках.
2. Первый признак подобия треугольников.
3. Свойство пересекающихся хорд.
4. Докажите, что в подобных треугольниках биссектрисы, проведенные из вершин соответственных углов, относятся как соответственные стороны.
|
Билет №8.
1. Лемма о подобных треугольниках.
2. Теорема Птолемея.
3. Свойство касательной и секущей.
4. Докажите, что в подобных треугольниках высоты, проведенные из вершин соответственных углов, относятся как соответственные стороны.
|
Билет №9.
1. Теорема Фалеса.
2. Третий признак подобия треугольников.
3. Свойство медиан треугольника.
4. Докажите, что средняя линия трапеции делит ее диагональ пополам.
|
Билет №10.
1. Подобные треугольники.
2. Второй признак подобия треугольников.
3. Свойство биссектрисы треугольника.
4. Докажите, что отношение периметров подобных треугольников равно коэффициенту подобия.
|
Билеты к зачету по геометрии: Итоги главы 3 (к учебнику Мерзляк А.Г. 8 класс).
Билет №1.
1. Синус острого угла прямоугольного треугольника.
2. Лемма (свойство высоты прямоугольного треугольника).
3. Основное тригонометрическое тождество.
4. Решите прямоугольный треугольник АВС (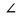 С=900) по известным элементам: АВ=8см, С=900) по известным элементам: АВ=8см, 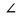 А=440. А=440.
|
Билет №2.
1. Косинус острого угла прямоугольного треугольника.
2. Теорема о метрических соотношениях в прямоугольном треугольнике.
3. Как связаны между собой 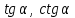 ? ?
4. Решите прямоугольный треугольник АВС (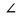 С=900) по известным элементам: АС=12см, С=900) по известным элементам: АС=12см, 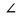 А=570. А=570.
|
Билет №3.
1. Тангенс острого угла прямоугольного треугольника.
2. Теорема Пифагора .
3. Как связаны между собой 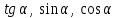 ? Как связаны между собой ? Как связаны между собой 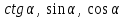 ? ?
4. Решите прямоугольный треугольник АВС (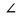 С=900) по известным элементам: АВ=14см, АС=8см. С=900) по известным элементам: АВ=14см, АС=8см.
|
Билет №4.
1. Котангенс острого угла прямоугольного треугольника.
2. Теорема Пифагора.
3. Чему равен 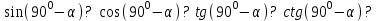
4. Решите прямоугольный треугольник АВС (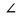 С=900) по известным элементам: ВС=8см, АС=14см. С=900) по известным элементам: ВС=8см, АС=14см.
|
Билет №5.
1. Синус острого угла прямоугольного треугольника.
2. Лемма (свойство высоты прямоугольного треугольника).
3. Основное тригонометрическое тождество.
4. Решите прямоугольный треугольник АВС (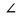 С=900) по известным элементам: АВ=8см, С=900) по известным элементам: АВ=8см, 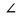 А=440. А=440.
|
Билет №6.
1. Косинус острого угла прямоугольного треугольника.
2. Теорема о метрических соотношениях в прямоугольном треугольнике.
3. Как связаны между собой 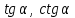 ? ?
4. Решите прямоугольный треугольник АВС (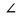 С=900) по известным элементам: АС=12см, С=900) по известным элементам: АС=12см, 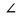 А=570. А=570.
|
Билет №7.
1. Тангенс острого угла прямоугольного треугольника.
2. Теорема Пифагора.
3. Как связаны между собой 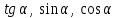 ? Как связаны между собой ? Как связаны между собой  ? ?
4. Решите прямоугольный треугольник АВС (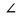 С=900) по известным элементам: АВ=14см, АС=8см. С=900) по известным элементам: АВ=14см, АС=8см.
|
Билет №8.
1. Котангенс острого угла прямоугольного треугольника.
2. Теорема Пифагора.
3. Чему равен 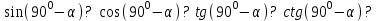
4. Решите прямоугольный треугольник АВС (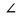 С=900) по известным элементам: ВС=8см, АС=14см. С=900) по известным элементам: ВС=8см, АС=14см.
|
Билет №9.
1. Синус острого угла прямоугольного треугольника.
2. Лемма (свойство высоты прямоугольного треугольника).
3. Основное тригонометрическое тождество.
4. Решите прямоугольный треугольник АВС (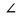 С=900) по известным элементам: АВ=8см, С=900) по известным элементам: АВ=8см, 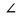 А=440. А=440.
|
Билет №10.
1. Косинус острого угла прямоугольного треугольника.
2. Теорема о метрических соотношениях в прямоугольном треугольнике.
3. Как связаны между собой 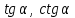 ? ?
4. Решите прямоугольный треугольник АВС (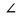 С=900) по известным элементам: АС=12см, С=900) по известным элементам: АС=12см, 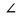 А=570. А=570.
|
Билеты к зачету по геометрии: Итоги главы 4 (к учебнику Мерзляк А.Г. 8 класс).
Билет №1.
1. Окружность описанная около многоугольника.
2. Сумма углов выпуклого п-угольника.
3. Площадь прямоугольного треугольника.
 4. Найти площадь 4. Найти площадь
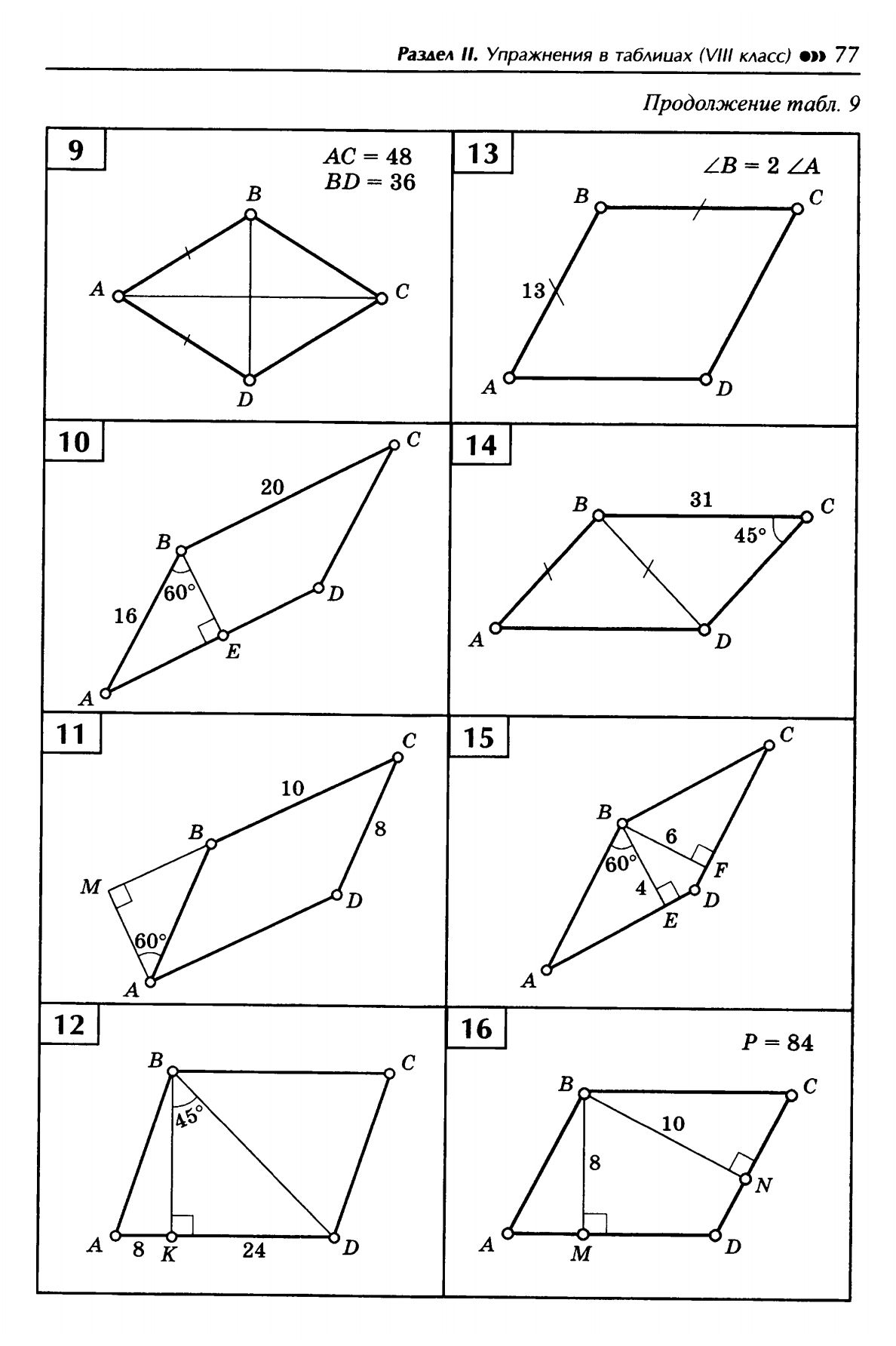
|
Билет №2.
1. Окружность вписанная в многоугольник.
2. Площадь параллелограмма.
3. Докажите, что медиана треугольника разбивает его на два равновеликих треугольника.
4. Найти площадь
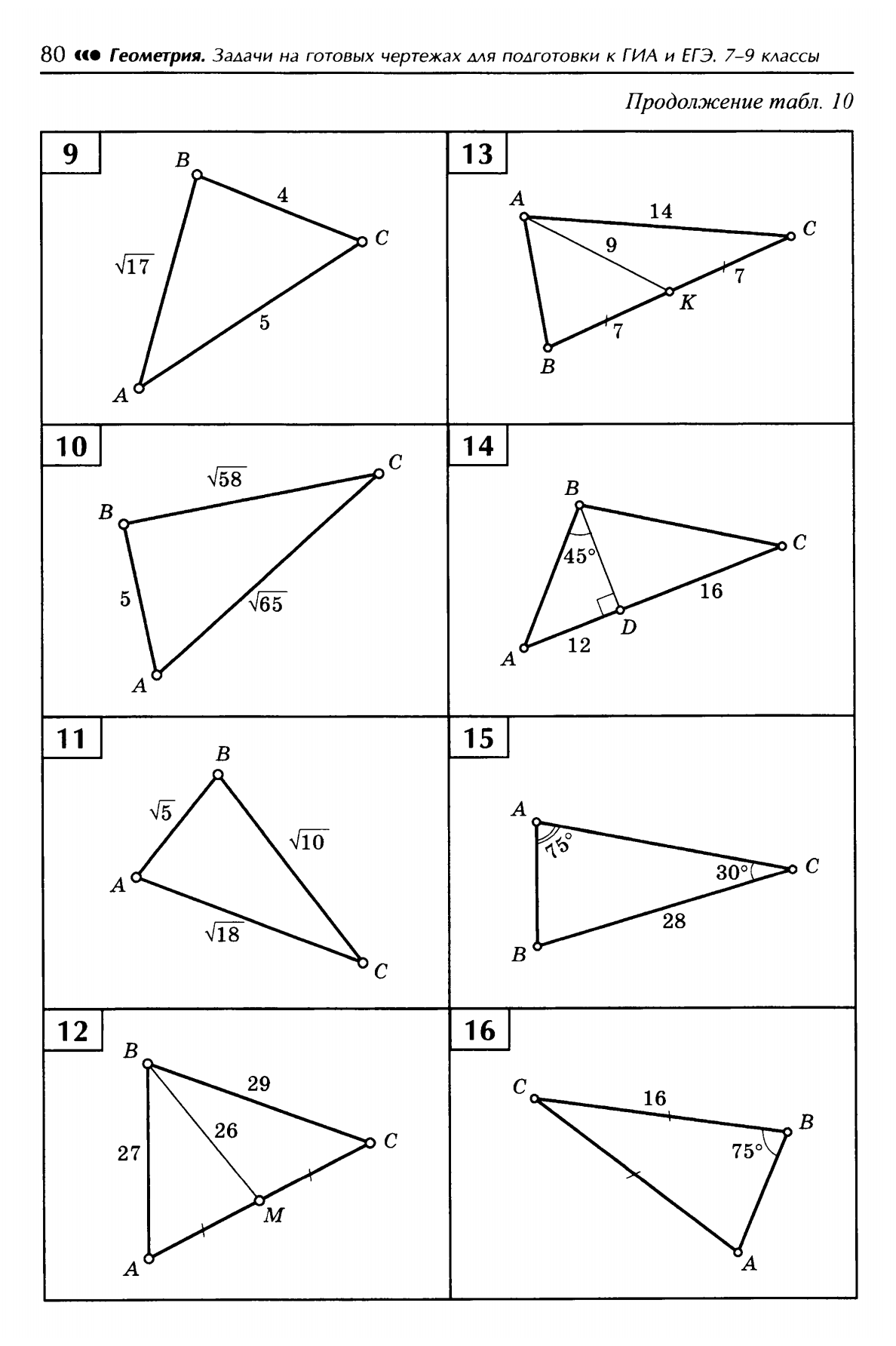
|
Билет №3.
1. Площадь многоугольника.
2. Площадь трапеции.
3. Площадь равностороннего треугольника со стороной а.
 4. Найти площадь 4. Найти площадь

|
Билет №4.
1. Равновеликие многоугольники.
2. Площадь треугольника.
3. Площадь ромба.
4. Найти площадь
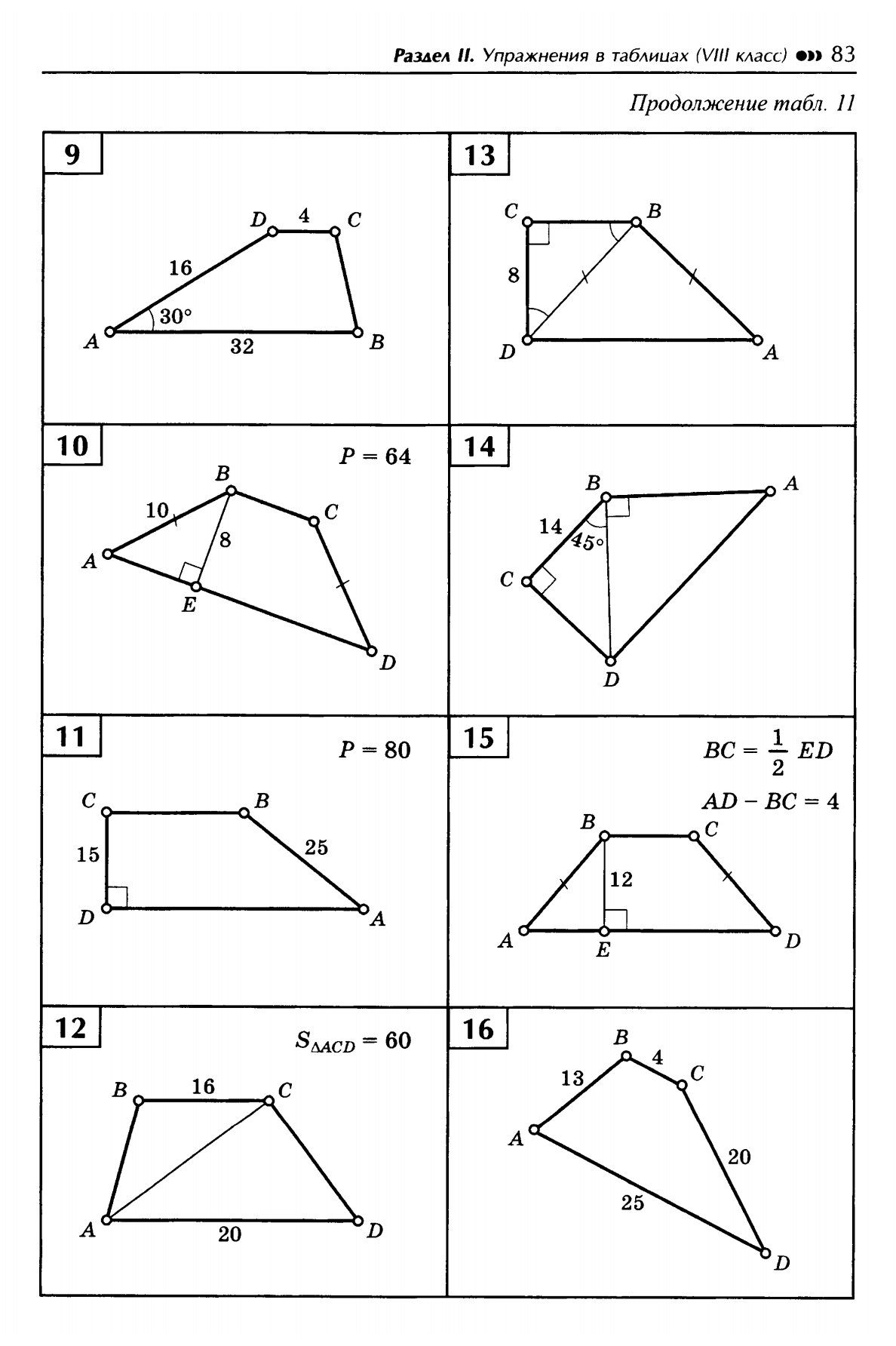
|
Билет №5.
1. Окружность описанная около многоугольника.
2. Сумма углов выпуклого п-угольника.
3. Площадь прямоугольного треугольника.
 4. Найти площадь 4. Найти площадь
 
|
Билет №6.
1. Окружность вписанная в многоугольник.
2. Площадь параллелограмма.
3. Докажите, что медиана треугольника разбивает его на два равновеликих треугольника.
4. Найти площадь

|
Билет №7.
1. Площадь многоугольника.
2. Площадь трапеции.
3. Площадь равностороннего треугольника со стороной а.
 4. Найти площадь 4. Найти площадь

|
Билет №8.
1. Равновеликие многоугольники.
2. Площадь треугольника.
3. Площадь ромба.
4. Найти площадь

|
 |
|
|
 Скачать 0.72 Mb.
Скачать 0.72 Mb.

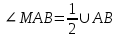 и
и 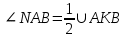 .
.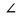 С=900) по известным элементам: АВ=8см,
С=900) по известным элементам: АВ=8см, 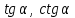 ?
?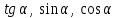 ? Как связаны между собой
? Как связаны между собой 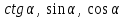 ?
?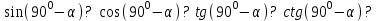
 4. Найти площадь
4. Найти площадь 

 4. Найти площадь
4. Найти площадь 
