Бинарные отношения в курсе математики начальной школы
 Скачать 55.66 Kb. Скачать 55.66 Kb.
|
|
Бинарные отношения в курсе математики начальной школы В настоящее время учащимся І–ІV классов в наглядной и конкретной форме знакомятся с такими важными математическими понятиями, как число и нуль, овладевают операциями над этими числами. Учитель, строя процесс обучения, должен опираться на эти операции и понятия. В процессе вычислительных навыков и в связи с решением задач различных видов, происходит усвоение первоначальных представлений о бинарных отношениях. «Бинарным отношением между элементами множеств X и У называется всякое подмножество декартового произведения X и У» [1]. Бинарное отношение условно обозначаются заглавными буквами латинского алфавита: P, R, G, N, D, C и др. Множество первых компонентных пар принадлежащих отношению P, называется областью определения отношения P, а множество вторых компонентных пар – областью значений отношения Р. Если элемент х принадлежит множеству X, а элемент у – множеству У, и элемент х находится в отношении P с элементом у, то пишут: xPy. Запись xPy читают: «Элемент х находится в отношении P с элементом у». В математике существуют отношения между элементами одного и того же множества. «Отношением во множестве X называются соответствия между элементами этого множества X» [2]. Отношения бывают самые разные. Например: множество стран мира: «Страна х больше страны у»; «В стране х население меньше, чем в стране у»; «Страны х и у имею общую границу» и т.д. Отношения между людьми: «х отец у»; «у и х – друзья»; «х учит у» – и т.д. Этот список возможных отношений можно долго продолжать. Отношение f можно изобразить наглядно. Например: между элементами двух множеств. Девочки, живущие, в одной комнате общежития составили, график дежурства на неделю, чередуясь, каждый день. Составьте граф график, таблицу дежурства между Камила, Багила, Пакизат, Зарина. А = {пн.; вт.; ср.; чт.; пт.; сб.; вс.} В = {Камила, Багила, Пакизат, Зарина} Р = Быть дежурной а P b а Î А; b Î В Р = {(пн.; пт. Камила); (вт; сб Багила); (ср; вс Пакизат); (чт Зарина)} Указанное отношение Р можно изобразить: а) при помощи графа; 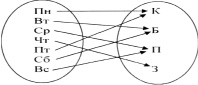 б) при помощи графика 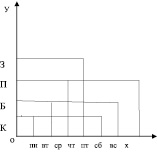 в) при помощи таблицы 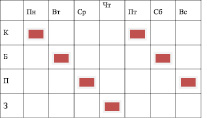 Например: Между элементами одного и того же множества. Между элементами множества Х = {1; 2; 3; 4} существует отношение «число х меньше числа у», причем элементы х и у принадлежат множеству X. Х = {1;2;3;4} Р = «число х меньше числа у» х, у Î X Р = {<1; 2>; <1; 3>; <1; 4>; <2; 3>; <2; 4>; <3; 4>} а) изображение при помощи графа. 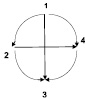 б) при помощи графика 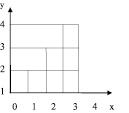 в) составлением таблицы 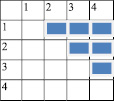 Из всего вышеизложенного следует, что отношения между элементами одного и того же множества задаются теми же способами, что отношения между элементами двух различных множеств. Отличия лишь в графах. Также как у других математических понятий у отношений существуют свои основные свойства: 1. Отношение R называется рефлексивным, если для любого x из множестваX истинно х R х (каждый элемент х Î Х находится в отношении R с самим собой). 2. Отношение R называется антирефлексивным, если ни один элемент х. Из множества X не находится в отношении R с самим собой. Отношение R называется симметричным, если для любых элементов х и y из множества X из xRy следует yRx. 3. Отношение R называется асимметричным, если ни для каких элементов х и у из множества X не может случиться что одновременно и xRy, и yRx. 4. Отношение R антисимметрично, если хRу и уRх одновременно выполняются в том и только в том случае, когда х = у. 5. Отношение R называется транзитивным, если для любых элементов х, y, z из множества X из того, что xRy и yRx следует xRz. Рассмотренные теоретические положения находят свое отражение на страницах учебников математики для I–IV классов общеобразовательной школы. В традиционном обучении вопросу отношений уделяется мало внимания. Чаще всего некоторые задания, связанные с пониманием отношений выступают в качестве иллюстративного материала. Так, например, отношения равенства и неравенства вводятся в I классе, однако изучение их простейших свойств передвигается в курс алгебры, тогда как потребность в применении этих свойств возникает во всех классах от I–IV. В традиционном курсе математики практически не рассматриваются двучленные отношения, отношения между элементами двух множеств. Значительно расширены возможности использования бинарных отношений и их свойств в альтернативных учебных программах обучения младших школьников математике – это в курсе математики, разработанный под руководством В.В. Давыдова [3]; в курсе математики, разработанный Н.Б. Истоминой [4]; в курсе математики Л.Г. Петерсон, Н.Я. Виленкин [5] и др. Система учебных заданий, представленных, в названных источниках отражает, различные примеры отношений: в одном случае они характеризуют содержание учебного курса (К.И. Нешков, В.Н. Рудницкая, А.М. Пышкало «Математика I, ІІ, ІІІ класс» В.В. Давыдов «Математика I»), в других являются иллюстративным материалом, только в расширенном варианте по сравнению традиционным. Но во всех программах развивающие возможности таких заданий ставятся во главу угла. Вывод: Используя упражнения, описанные выше, в учебном процессе, педагог побуждает учеников к поиску, чем вызывает развитие мыслительных процессов. Ученики в результате выполнения многих практических, творческих видов задания, научатся сравнивать две группы предметов, устанавливать в какой группе предметов больше (меньше) или столько же предметов в одной группе сколько и в другой. В итоге они освоят такие слова и словосочетания, как «больше», «меньше», «столько же», «столько, сколько» и будут упражняться во время сравнения в конкретных практических действиях. Следовательно, каждое из заданий имеет свои развивающие функции, которые направлены на формирование у младших школьников понятий об отношениях. Задания для выполнения Между элементами двух множеств составьте бинарное отношение «Животное А ниже животного В». Постройте граф, график, таблицу этого отношения и опишите, какими свойствами оно обладает, если А={лягушка, волк, ёж, корова}, В={кот, баран, жираф} Ответы прислать до 25.05.2020 на почту olklimov@bk.ru (в теме письма указать свою фамилию) |
