методика изучения алгебраического материала. Методика изучения алгебраического материала. Общая характеристика алгебраического материала в курсе математики начальной школы
 Скачать 116.5 Kb. Скачать 116.5 Kb.
|
|
ОБЩАЯ ХАРАКТЕРИСТИКА АЛГЕБРАИЧЕСКОГО МАТЕРИАЛА В КУРСЕ МАТЕМАТИКИ НАЧАЛЬНОЙ ШКОЛЫ Достаточно долгое время в психологии господствовало мнение (например, П.П. Блонского), что элементы алгебры следует изучать не в начальных, а в старших классах в силу особенностей мышления младшего Школьника, неспособности его к образованию абстракций более высокого уровня. В последние годы исследованиями советских психологов (П.Я. Гальперин, В.В. Давыдов, Д.Б. Эльконин и др.) и педагогов (А.И. Маркушевич, А.М. Пышкало и др.) было установлено, что познавательные возможности младших школьников при традиционной системе обучения значительно занижались. Дети 6–10 лет при определенной организации обучения могут полноценно усвоить содержание некоторых алгебраических понятий. При этом у них раньше, чем обычно, возникают предпосылки к теоретическому рассуждению (особенно в связи с введением буквенной символики). На основании этого алгебраический материал был включен в программу по математике для начальных классов в 1969 г. Включение в содержание обучения элементов алгебры, особенно упражнений с функциональным содержанием, позволяет увидеть динамичность явлений реального мира, взаимную обусловленность и связь величин, а это оказывает большое влияние на формирование мировоззрения учащихся. Изучение алгебраического материала способствует развитию у учащихся таких логических приемов, как анализ и синтез, обобщение и конкретизация, индукция и дедукция. Введение элементов алгебры имеет большое значение для совершенствования системы начального математического образования, расширения арсенала математических средств, используемых школьниками при решении задач. Буквенная символика, вводимая в начальных классах, и связанное с ней понятие переменной способствуют обобщению знаний о числах, свойствах арифметических действий. Таким образом, проводится работа по функциональной пропедевтике одного из важнейших понятий современной математики — понятия соответствия. Использование уравнений для решения задач позволяет существенно изменить всю систему обучения решению задач. В целом же алгебраический материал в курсе математики начальной школы выполняет вспомогательную функцию при изучении основного (арифметического) содержания программы. МЕТОДИКА ИЗУЧЕНИЯ ЧИСЛОВЫХ ВЫРАЖЕНИЙ Понятие математического выражения (или просто выражения), изучаемое в начальных классах, имеет большое значение. Так, это понятие помогает учащимся овладеть вычислительными навыками. Действительно, часто вычислительные ошибки связаны с непониманием структуры выражений, нетвердым знанием порядка выполнения действий в выражениях. Усвоение понятия выражения обуславливает формирование таких важных математических понятий, как равенство, неравенство, уравнение. Умение составлять выражение для решения задачи необходимо для овладения умением решать задачи алгебраическим способом, т. е. с помощью составления уравнений. С первыми выражениями — суммой и разностью — дети знакомятся при изучении сложения и вычитания в концентре «Десяток». Не используя специальных терминов, первоклассники производят вычисления, записывают выражения, читают их, заменяют число суммой, основываясь на наглядных представлениях. При этом выражение 4 + 3 они читают следующим образом: «к четырем прибавить три» или «4 увеличить на 3», а выражение 4 – 3 — «из четырех вычесть три» или «4 уменьшить на 3». Находя значения выражений, состоящих из трех чисел, которые соединены знаками сложения и вычитания, учащиеся фактически пользуются правилом порядка выполнения действий в неявном виде и выполняют первые тождественные преобразования выражений. Познакомившись с выражениями вида a + b, первоклассники сначала употребляют термин «сумма» для обозначения числа, получающегося в результате сложения, т. е. сумма трактуется как значение выражения. Затем с появлением более сложных выражений например вида (a + b)– c, появляется необходимость иного понимания термина «сумма». Выражение a + b называется суммой, а его компоненты — слагаемыми. При введении выражений вида a – b, a · b, a : b поступают аналогично. Сначала разностью (произведением, частным) называют значение выражения, а затем само выражение. Одновременно учащимся сообщают названия его компонентов: уменьшаемое, вычитаемое, множители, делимое и делитель. Например, в равенстве 9 – 4 = 5 9 — уменьшаемое, 4 — вычитаемое, 5 — разность. Запись 9 – 4 также называется разностью. Можно вводить эти термины в другой последовательности: предложить учащимся записать пример 9 – 4, пояснив, что записана разность, и вычислить, чему равна записанная разность. Учитель вводит название полученного числа: 5 — тоже разность. Другие числа при вычитании называются: 9 — уменьшаемое, 4 — вычитаемое. З 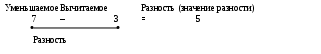 апоминанию новых терминов способствуют плакаты вида апоминанию новых терминов способствуют плакаты видаДля закрепления этих терминов предлагаются упражнения вида: «Вычислите сумму чисел; запишите сумму чисел; сравните суммы чисел (вставьте знак >, < или = вместо * в запись 4 + 3 * 5 + 1 и прочтите полученную запись); замените число суммой одинаковых (разных) чисел; заполните таблицу; составьте по таблице примеры и решите их». Важно, чтобы дети поняли, что при вычислении суммы производится указанное действие (сложение), а при записи суммы получаем два числа, соединенных знаком плюс. На следующем этапе усвоения понятия выражения учащиеся знакомятся с выражениями, в которых используются скобки: (10 – 3) + 4, (6 – 2) + 5. Они могут быть введены посредством текстовых задач. Возможен и другой подход. Учитель предлагает составить на наборном полотне сумму и разность чисел 10 и 3, используя карточки, на которых записаны эти числа и знаки действий. Затем составленную учениками разность 10 – 3 учитель заменяет подготовленной заранее карточкой с этой разностью. Следующее задание: составить выражение (на этом этапе обучения о нем говорят как о примере), используя разность, число 4 и знак +. При чтении полученного выражения обращается внимание на то, что его компонентами являются разность и число. «Чтобы было заметно, — говорит учитель, — что разность является слагаемым, ее заключают в скобки». Самостоятельно конструируя выражения, дети осознают их структуру, овладевают умением читать, записывать, вычислять их значения. Вводятся термины «математическое выражение» (или просто «выражение») и «значение выражения». Определения этих терминов не даются. Записав несколько простейших выражений: сумм, разностей, учитель называет их математическими выражениями. Предложив вычислить эти примеры, он объявляет, что числа, полученные в результате вычисления, называются значением выражения. Дальнейшая работа над числовыми выражениями состоит в том, что дети упражняются в чтении, записи под диктовку, составлении выражений, заполнении таблиц, широко используя при этом новые термины. Затем изучается порядок выполнения действий. Выражения вида: 37 – 24 + 3, 63 : 9 · 4 знакомы учащимся: они их читали, записывали под диктовку, вычисляли их значения, еще не зная правил порядка выполнения действий, но уже неявно их используя. С выражениями вида a + b · c, a – b · c учащиеся встречаются впервые. В этом случае может быть создана проблемная ситуация. Учащимся предлагается вычислить значение выражения 49 – 35 : 7. Получив различные значения этого выражения, учащиеся сталкиваются с проблемой: какое же из них считать верным. Разрешая ее, учитель формулирует правило порядка выполнения действий в таких выражениях. Важно подчеркнуть, что при выполнении действий в таких выражениях условились выполнять вначале умножение и деление, а затем сложение и вычитание. Это упрощает запись выражений: произведение и частное записываются без скобок. Чтобы ученики осознанно усвоили правила порядка выполнения действий, наряду с тренировочными упражнениями на нахождение значения выражения полезны специальные задания: «Вычислите с пояснениями (45 – 30) : 5 и 45 – 30 : 5; 15 · 3 – 28 : 7; расставьте скобки так, чтобы значение выражения равнялось 105». Необходимо сформировать у учащихся еще одно практическое умение — читать составные выражения. Вначале, выполняя конкретные операции над множествами, ученики осознают смысл сложения и вычитания как «прибавить» и «вычесть», поэтому выражения они читают следующим образом: «к семи прибавить два», «из пяти вычесть один». В дальнейшем понимание действий сложения и вычитания углубляется. Выражения 7 + 2, 6 – 1 читаются следующим образом: «7 увеличить на 2», «6 уменьшить на 1». С введением названий компонентов действий эти выражения читаются по-другому: «сумма чисел 7 и 2», «разность чисел 6 и 1». Затем учащиеся учатся читать составные выражения, в которых действия выполняются в том порядке, в котором они записаны. Так, выражение 4 + 2 + 1 учащиеся читают: «к четырем прибавить два и к полученному числу прибавить один», а выражение 24 : 3 · 2 — «двадцать четыре разделить на три и полученный результат умножить на два». Для чтения сложных выражений учащиеся используют следующий алгоритм: 1) определяют, какое действие в выражении выполняется последним; 2) вспоминают названия компонентов этого действия; 3) называют, чем выражены его компоненты. Для обучения чтению выражений используется методика работы «по образцу». Например, учитель показывает, как читается выражение 3 + 7: это сумма, в которой первое слагаемое — 3, а второе слагаемое — 7. При чтении сложного выражения 16 · 4— 10 учитель рассуждает так: «В выражении 16 · 4 + 10 последним выполняется действие сложения, значит, это выражение — сумма; компоненты этого действия — слагаемые; первое слагаемое выражено произведением, в котором сомножители — числа 16 и 4, а второе слагаемое — число 10». (Здесь алгоритм использовался два раза.) Формирование понятия числового выражения тесно связано с обучением учащихся решению текстовых задач. Поясним это на конкретном примере. Учащимся предлагается условие задачи: «В магазин привезли 3 ящика помидоров по 10 кг в каждом и 6 ящиков огурцов по 15 кг в каждом». Условие задачи содержит 4 числовых данных. Вначале ученики выбирают произвольные пары значений и записывают следующие простые выражения, которые можно объяснить исходя из условия задачи: 3 + 6 — общее количество ящиков, привезенных в магазин; 10 · 3 — масса всех помидоров; 15 · 6 — масса всех огурцов; 6 – 3 — на столько больше привезли ящиков огурцов, чем помидоров; 6 : 3 — во столько раз больше привезли ящиков огурцов, чем помидоров; 15 – 10 — на столько больше масса одного ящика огурцов, чем ящика помидоров. Затем учитель предлагает учащимся записать сложные выражения, содержащие два и более действий, опираясь на составленные простые выражения. Выражение 6 · 15 – 3 · 10 соответствует данному условию и позволяет ответить на вопрос: «На сколько больше привезли в магазин огурцов, чем помидоров?» Выражение 15 · 6 + 10 · 3 соответствует вопросу: «Сколько всего овощей привезли в магазин?» Составление выражений по условию задачи должно вестись параллельно с составлением задач по выражению. С этой целью учащиеся выполняют ряд заданий. У Тани 6 карандашей, а у Оли 5. Какой вопрос надо поставить к условию задачи, чтобы она решалась так: 6 – 5. В первый день турист прошел 20 км, во второй день — 14 км. Сколько километров он прошел за два дня? Составьте похожую задачу, которая решается так: 18— 11. Составьте задачу, в которой надо узнать, во сколько раз 15 меньше 45. Составьте задачу по выражению 18 : 3. Заметим, что по выражению 18 : 3 может быть составлена задача на кратное сравнение, на деление по содержанию, на деление на равные части, на нахождение неизвестного множителя. В такой же последовательности проводится работа и со сложными выражениями (составными задачами): 1) поставьте вопрос к условию задачи, чтобы она решалась данным выражением; 2) составьте задачу по выражению, аналогичную только что решенной; 3) составьте задачу данного вида; 4) составьте задачу по выражению. ФОРМИРОВАНИЕ ПОНЯТИЯ ПЕРЕМЕННОЙ Введение буквенной символики, осуществляемое в начальном курсе математики, позволяет познакомить учащихся с основными понятиями современной математики: переменной, уравнением, неравенством и способствует развитию функционального мышления, так как с понятием переменной тесно связана идея функциональной зависимости. Первый этап формирования представлений о переменной величине реализуется в первом классе, когда ученики начинают упражняться в выполнении заданий с «окошечками» (пропусками). Окошечко не случайно используется для раскрытия понятия переменной, так как в современной трактовке оно обозначает знак, играющий роль «местодержателя» для имен определенного заданного множества (область значений переменной) — множества целых неотрицательных чисел в начальном курсе математики. В учебнике математики для первого класса встречаются записи вида 3 + =5; + = 6; 5 > ; 0 > , задания по которым могут быть сформулированы в разной форме, например: «Какое из чисел нужно записать в окошечко, чтобы получилась верная запись? Восстанови в записи пропущенное число». Вначале при выполнении таких упражнений используются наглядные пособия. Затем, по мере накопления знаний, учащиеся отказываются от них. Так, при нахождении числа, которое надо вставить в «окошечко» в записи 3 + = 5, предлагается попробовать подставить в «окошечко» поочередно числа от 0 до 4. Вначале такая работа проводится на наборном полотне. Подставляя в «окошечко» карточки с соответствующими числами, ученики выясняют, верна или неверна запись, либо с помощью наглядных пособий, либо опираясь на знание таблиц сложения. Затем примеры такого типа решаются с устным разбором. Раскрытию понятия переменной способствует и работа по заполнению таблиц:
Такие упражнения способствуют не только совершенствованию вычислительных навыков, но и выработке представления о переменной и множестве ее значений. После заполнения таблицы учащимся можно задать следующие вопросы: «Какие значения принимают уменьшаемое; вычитаемое; разность? Изменяется ли уменьшаемое; вычитаемое; разность? Как они изменяются?» В некоторых таблиц значения одного из компонентов могут быть постоянными. Таким образом, дети видят, что переменная может принимать не только различные, но и одинаковые значения. Переменная присутствует и в записях вида + 1, с которыми первоклассники встречаются при изучении различных случаев сложения и вычитания. Следует обратить внимание детей на эти записи объяснить, что в «окошечко» можно подставлять любое из изученных чисел. Так, при изучении прибавления двух может использоваться запись + 1 + 1. Непосредственно перед введением буквенной символики полезно рассмотреть простые арифметические задачи с пропущенными числовыми данными. Подбирая числа, учащиеся получают арифметические задачи, решение которых записывают в виде таблицы (последняя строка таблицы — выражение, являющееся решением задачи). Второй этап формирования понятия переменной — введение букв как символов для обозначения переменной. На этом этапе широко используется сочетание индуктивного и дедуктивного методов. Осуществляя переход от числового выражения к буквенному и от буквенного к числовому, учащиеся тем самым обобщают смысл числовых выражений и конкретизируют его, подставляя вместо букв числовые значения. Для раскрытия смысла букв как символов для обозначения переменной можно использовать однотипные числовые выражения (суммы) и простые односюжетные арифметические задачи. В последнем случае необходимо акцентировать внимание учащихся не на ответе, а на выражениях, соответствующих данным задачи: числовые компоненты могут быть различными, но их всегда два, и выражение записывается в виде суммы. На этом этапе учащиеся выполняют разные по форме и содержанию задания. Найти числовые значения буквенных выражений при разных значениях букв (задание представлено в виде таблицы). Подобрать числовые значения букв, входящих в выражение, значение которого задано. Решить простую задачу с буквенными данными. (Работа над этими задачами осуществляется в такой последовательной: а) в условие подставляются конкретные числовые значения; б) решением этих задач являются числовые выражения; в) буквенные выражения выступают как обобщенная запись решения всех задач числовыми с данными определенного вида.) Аналогично вводится запись разности двух чисел. Однако в этом случае дети учатся устанавливать, какие числовые значения могут принимать буквы, входящие в разность, что фактически является. установлением области допустимых значений переменных. На последнем (третьем) этапе буквенная символика выступает как средство обобщения знаний учащихся о свойствах действий, взаимосвязях компонентов действий. Обобщение происходит на основе неполной индукции. Учащиеся знакомятся с некоторым множеством однородных выражений. С помощью анализа, сравнения, синтеза они устанавливают общие и существенные свойства этих выражений, т.е. приходят к обобщенным теоретическим знаниям. Поэтому использование буквенной символики как средства обобщения формируемых знаний может осуществляться только тогда, когда учащиеся многократно наблюдали обобщаемые свойства, зависимость, формулировали их и использовали при выполнении различных упражнений. Ученики приходят к пониманию, что использование буквенной символики для записи определенных зависимостей, свойств, отношений означает, что изучаемые зависимости справедливы для любых значений переменных. С этой целью следует предусмотреть упражнения, выполняя которые учащиеся овладевают умениями записывать с помощью букв свойства арифметических действий, взаимосвязи компонентов действий, читать свойства и зависимости, записанные с помощью буквенной символики, выполнять тождественные преобразования выражений с переменными на основе знания свойств действий, смысла арифметических действий, доказывать справедливость равенства или неравенства, опираясь на знание элементов теории. Приведем примеры таких упражнений. Для усвоения переместительного свойства умножения можно предложить следующие задания: сравните выражения: 15 · 20 и 20 · 15, 40 · 11 и 11 · 40; замените буквы числами так, чтобы получились верные равенства: 23 · a = a · 23. При выполнении этого задания учитывается, что одна и та же буква принимает в равенстве одно и то же значение; чему равно произведение 124 · 362, если 362 · 124 = 44 888? Найдите значение выражения c · m, если m · c= 96 (m и c в обоих равенствах одинаковы); закончите запись m · n = n · m ... С целью формирования у учащихся умения доказывать справедливость полученных равенств или неравенств выполняются специальные упражнения. Например, требуется проверить равенство (a – b) · c = a · c – b · cили сравнить выражения a :(b· c) и a : b : c. Во всех этих случаях, после того как проведено доказательство, основанное на знании учащимися элементов теории, полезно предложить им убедиться в справедливости равенства или неравенства, придав буквам различные числовые значения. Лучше, если каждый ученик выберет произвольные числовые значения, тогда при проверке можно показать, что вывод, сделанный на основе применения общего правила, верен при любых значениях букв. УРАВНЕНИЯ В соответствии с программой в начальных классах рассматриваются уравнения первой степени с одним неизвестным вида: 7 + x = 10, x – 3 = 10 + 5, x · (17 – 10) = 70, x : 2 + 10 = 30. Уравнения в начальных классах рассматриваются как верные равенства, решение уравнения сводится к отысканию того значения буквы (неизвестного числа), при котором данное выражение имеет указанное значение. Нахождение неизвестного числа в таких равенствах выполняется на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. На подготовительном этапе к введению первых уравнений при изучении сложения и вычитания в пределах 10 учащиеся усваивают связь между, суммой и слагаемыми. Кроме того, к этому времени дети овладевают умением сравнивать выражение и число и получают первые представления о числовых равенствах вида: 6 + 4 = 10, 8 = 5 + 3. Большое значение в плане подготовки к введению уравнений имеют упражнения на подбор пропущенного числа в равенствах вида 4 + □ = 6, 5 – □ = 2, □ – 3 = 7 (II класс). В процессе выполнения таких упражнений дети привыкают к мысли, что неизвестным может быть не только сумма или разность, но и одно из слагаемых (уменьшаемое или вычитаемое). На первом этапе (III класс) происходит знакомство учеников с уравнением в ходе решения задачи отвлеченными числами, например такой: «К неизвестному числу прибавили 3 и получили 8. Найти неизвестное число». По данной задаче составляется пример с неизвестным числом, который может быть записан так: □ + 3 = 8. Затем учитель поясняет, что в математике принято обозначать неизвестное число латинскими буквами. Дается запись и чтение одной из букв — x (икс). Предлагается обозначить неизвестное число буквой и прочитать пример. Ставится цель научиться решать такие примеры. Учитель. Положите столько кружков, сколько получилось, когда к неизвестному числу прибавили 3. Сколько положили кружков? Ученик. 8 кружков. Учитель. Как получили число 8? Ученик. К неизвестному числу прибавили 3. Учитель. Покажите 3 кружка, которые прибавили к неизвестному числу кружков. Отодвиньте эти 3 кружка. Сколько кружков было сначала? Ученик. 5 кружков. Учитель. Как узнали, сколько было кружков? Ученик. Из всех кружков вычли 3 кружка. Учитель. Посмотрите на пример и скажите, что узнали. Ученик. Первое слагаемое. Учитель. Как нашли первое слагаемое? Ученик. Из суммы 8 вычли второе слагаемое 3. У x + 3 = 8 x = 8 – 3 x = 5 Проверка 5 + 3 = 8 8 = 8 читель на доске, а учащиеся в тетрадях записывают: Аналогично разбирается еще несколько примеров, в которых неизвестно первое или второе слагаемое. Учитель поясняет, что такие примеры называют уравнениями, что найти неизвестное число — значит решить уравнение. Определение уравнения и корня уравнения не дается в начальных классах. Учащиеся упражняются в чтении, записи и решении уравнений. Показывают разные формы чтения: «К какому числу надо прибавить 2, чтобы получилось 9?», «Первое слагаемое 4, второе неизвестно, сумма равна 7; чему равно второе слагаемое?» При решении первых уравнений дети опираются на операции над множествами, на знание состава числа, на понимание отношений между суммой и слагаемыми (каждое слагаемое меньше суммы). Постепенно учащиеся усваивают правило нахождения неизвестного слагаемого и в дальнейшем пользуются им при решении уравнений. Затем с помощью уравнений решают текстовые задачи на нахождение неизвестного слагаемого. Примерно в таком же плане рассматривается решение уравнения вида: х – 2 = 8, 10 – х = 4, а затем: х · 3 = 12, 5 · х = 10, х : 2 = 4, 6 : х = 3, которые решаются на основе связи между результатами и компонентами действий. Каждый раз на первом этапе, когда сами правила нахождения неизвестных компонентов еще усваиваются детьми, решение уравнений выполняется с опорой на операции над множествами, на сравнение данных чисел и искомого числа. Позже, на следующем этапе, уравнения решаются на основе знания правил нахождения неизвестного компонента. Усвоению правил нахождения неизвестных способствуют упражнения на сопоставление уравнений и их решений, например, таких: х + 8 = 10 и х – 8 = 10, х · 3 = 9 и х : 3 = 9 и т.п. С первых же шагов обучения решению уравнений приучают детей к тому, чтобы они выполняли проверку: найденное число подставляли в выражение, вычисляли его значение и сравнивали с тем значением, которое дано в уравнении. На втором этапе в процесс изучения включаются уравнения вида: х + 10 = 30 – 7, х + (45 – 17) = 40 и т.п. Для решения таких уравнений необходимы знания порядка действий в выражении, а также умения выполнять простейшие преобразования выражений. Первыми рассматриваются уравнения, в которых правая часть задается не числом, а числовым выражением, например: х + 25 = 50 – 14 или х + 25 = 12 · 3 и т.п. При решении подобных уравнений учащиеся вычисляют значение выражения в правой части, после чего уравнение сводится к простейшему. Например, решается уравнение х – 8 = 70 + 14. Учащиеся читают уравнение (разность неизвестного числа и 8 равна сумме чисел 70 и 14). Сначала вычисляют, чему равна сумма чисел 70 и 14 и записывают новое уравнение х – 8 = 84. Затем выражают неизвестное уменьшаемое (х = 84 + 8) и вычисляют его (х = 92). Проверяют, правильно ли решено уравнение. Для этого подставляют найденное значение буквы в выражение и вычисляют его значение (92 – 8 = 84), значение выражения в правой части уже вычисляли (70 + 14 = 84), далее сравнивают их (84 = 84); если значения выражений равны, уравнение решено верно. На протяжении длительного периода учащиеся упражняются в чтении, записи, решении и проверке таких уравнений, причем в левую и правую части их включаются простейшие выражения всех видов в различных сочетаниях. Далее включаются уравнения, в которых в виде числового выражения задан один из компонентов, например: х + (60 – 48) = 20, (35 + 8) – х = 30. Полезно учить читать эти уравнения с называнием компонентов (например: «Первое слагаемое неизвестно, второе выражено разностью чисел 60 и 48, сумма равна 20»). Чтобы прочитать уравнение, следует в выражении установить порядок действий, выделить последнее действие, вспомнить, называются числа при выполнении этого действия, и прочитать с названием компонентов и результата. Как видно, такое чтение требует анализа выражения, при этом сразу вычленяется неизвестный компонент и указывается, каким выражением задан известный компонент. Как и в предыдущем случае, сначала упрощают заданное выражение, а затем решают простейшее уравнение. Например, в уравнении (35 + 8) – х = 30 вычисляют, чему равно уменьшаемое и получают уравнение, равносильное первому: 43 – х = 30, которое дети умеют решать. При отработке умений решать уравнения рассматриваемой структуры, используют уравнения, решение которых опирается на знание связи между результатами и компонентами только действий сложения и вычитания; в IV классе — всех четырех действий. На третьем этапе (III класс) изучаются приемы решения наиболее сложных уравнений, в которых один компонентов — выражение, содержащее неизвестное число, например: (х + 8) – 13 = 15, 70 + (40 – х) = 96 и т.п., так как при решении уравнений данной структуры приходится дважды применять правила нахождения неизвестных компонентов. Haпример, рассматривают на уроке уравнение (12 – x) + 10 = 18. Учитель. Научимся решать такие уравнения. Очень важно правильно прочитать его. Какое действие выполняется последним в выражении слева? Ученик. Последнее действие — сложение. Учитель. Вспомните, как называются числа при сложении и прочитайте это уравнение. Ученик. Первое слагаемое выражено разностью 12 и х, второе слагаемое 10, сумма 18. Учитель (прикрепляет соответственно таблички с терминами «слагаемое», «сумма»). Куда входит неизвестное число? Ученик. В первое слагаемое. Учитель. Как найти первое слагаемое? Ученик. Чтобы найти первое слагаемое, надо из суммы вычесть второе (записывает на доске: 12 – х = 18 – 10; все учащиеся пишут в тетрадях). Учитель. Такие уравнения мы решали. Что теперь надо сделать? Ученик. Вычислить разность чисел 18 и 10 (пишет: 12 – х = 8). Учитель. Что здесь неизвестно и как найти это неизвестное число? Решайте самостоятельно. Надо проверить, верно ли вы нашли значение х. Что нужно для этого сделать? Ученик. Надо подставить вместо х его значение 4 (пишет: (12 – 4) + 10), вычислить (пишет: 18) и сравнить с числом в правой части (пишет: 18 = 18). Далее так же рассматривается уравнение 36 – (20 + х) = 10. Обучение решению уравнений этого вида требует длительных упражнений в анализе выражений и хорошего знания правил нахождения неизвестных компонентов. На первых порах полезны упражнения в пояснении решенных уравнений. Кроме того, следует чаще решать такие уравнения с предварительным выяснением, что неизвестно и какие правила надо вспомнить, чтобы решить данное уравнение. Такая работа предупреждает ошибки и способствует овладению умением решать уравнения. В IV классе учащиеся решают уравнения, которые включают сложные выражения с действиями первой и второй ступени. Методика работы над ними аналогична рассмотренной. ИЗУЧЕНИЕ НЕРАВЕНСТВ С ПЕРЕМЕННОЙ В программе не ставится задача обучения учащихся методам решения неравенств. Однако очень часто на практике, например при изучении отношения порядка на множестве натуральных чисел, используются упражнения такого вида: < 4; > 7; 3 > . Учащимся предлагается найти число, которое нужно вставить в «окошечко», чтобы получилась верная запись (верное неравенство). В дальнейшем неравенства становятся более разнообразными, усложняется структура сравниваемых выражений. Неизвестное число сравнивается с выражением (24 – 6 < ), оно может выступать и одним из компонентов выражения (15 < 15 + , 10 – 3 < ). После введения букв как символов для обозначения переменной неравенство принимает вид: 2 · a < 8. Такие неравенства также решаются методом подбора. Для облегчения решения неравенств задания формулируются следующим образом: «Из ряда чисел 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 выбери те значения буквы a при которых верно неравенство a · 2 < 12». Затем упражнения усложняются. Ученики должны самостоятельно подобрать значения переменной, при которых данное неравенство будет верным: «Подбери такие числа, чтобы неравенства были верными: 12 + x < 15; a : 5 < 4». Хотя основным методом решения неравенств с переменном является метод подбора, в некоторых случаях, например при решении неравенства 5 + c > 5 + 2, ученик может, используя зависимость между компонентами и результатом сложения, сразу назвать 1–2 числа, удовлетворяющие неравенству. Однако и в этом случае он должен доказать, что нашел числа правильно, т. е. подставить данные числа в неравенство вместо буквы. В дальнейшем учащихся обучают следующему, рациональному способу решения неравенств: сперва составляют и решают соответствующее неравенство, например, для неравенства x ·5 < 40 решают уравнение x ·5 = 40 x = 40 : 5 x = 8. Следовательно, для неравенства подходят значения x < 8, т.е. 0, 1, 2, 3, 4, 5, 6, 7. |
