БИОСТАТИСТИКА_РК1_Рамазан_Ақниет. Биостатистика пнінен 1 аралы баылау сратары
 Скачать 6.09 Mb. Скачать 6.09 Mb.
|
«Биостатистика» пәнінен 1- аралық бақылау сұрақтары. Биостатистика пәні, мақсаты мен міндеттері. Статистика – қоғамдық ғылым, ол қоғамдық құбылыстардың сандық және сапалық өзгерістерінің өзара байланысын зерттейді. Яғни, статистиканың негізгі мақсаты – қоғамдағы өзгерістердің заңдылығын анықтау. Статистиканың теориялық негізі ықтималдықтар теориясы мен математикалық статистиканың заңдарына сүйенеді. Математикалық статистиканың биологияда, медицинада қолданылатын бөлімі биостатистика деп аталады, оның құрамына медициналық статистика кіреді. Медициналық статистика – қоғам денсаулығын және денсаулық сақтауды зерттейтін ғылым. «Статистика» термині латынның «статус» (status) деген сөзінен шыққан, қазақша «күй», «хал-жағдай» деген мағынаны береді. Медициналық статистиканың үш бөлімі бар: 1) халық денсаулығының статистикасы; 2) денсаулық сақтау ісінің статистикасы; 3) дәлелдік медицина статистикасы. Медициналық статистиканың мақсаттары: - халық денсаулығының өзгерушілігінің ерекшеліктерін анықтау және оған әсер ететін факторларды табу; - емдеу-сауықтыру мекемелерінің санын, жұмысының нәтижелерін, емдеу-сауықтыру қызметтерінің тиімділігін, дәрігердің және басқа да медицина қызметкерлерінің жұмысын зерттеу; - тәжірибелік, клиникалық, гигиеналық және лабораториялық жұмыстардың нәтижелерін анықтау. Биостатистиканың негізгі мақсаты – тірі табиғатта болып жатқан үрдістерді дұрыс сандық бағалауға үйрету. Биостатистиканың негізгі міндеті – биологиялық жиынтықтарды бағалау үшін негізгі статистикалық критерийлермен таныстыру және оларды қолдануды үйрету. Статистикалық зерттеулердің негізгі кезеңдері мынадай: 1. Зерттеудің жоспары мен бағдарламасын жасау. 2. Мәліметтер жинау немесе статистикалық тіркеу. 3. Мәліметтерді өңдеу және топтастыру. 4. Мәліметтерді талдау және қорытынды жасау. 5. Зерттеудің нәтижелерін іс жүзінде енгізу.  Статистикалық зерттеулердің негізгі кезеңдері. Зерттеу жоспары мен бағдарламасын құрайтын элементтер. Статистикалық зерттеулердің негізгі кезеңдері мынадай: 1. Зерттеудің жоспары мен бағдарламасын жасау. 2. Мәліметтер жинау немесе статистикалық тіркеу. 3. Мәліметтерді өңдеу және топтастыру. 4. Мәліметтерді талдау және қорытынды жасау. 5. Зерттеудің нәтижелерін іс жүзінде енгізу. Статистикалық зерттеудің жоспары мен бағдарламасын жасау – зерттеудің негізгі мақсаты мен міндеттерін анықтаудан басталады. Зерттеу не үшін жүргізіледі деген сұрақты зерттеу мақсаты айқындайды. 1-нші кезеңде мәселе айқындалып, зерттеу тақырыбы тұжырымдалады. Ал жоспарда мақсатқа жету үшін қандай міндеттер, жұмыстар жүргізілуі керек екендігі көрсетіледі. Алдымен, зерттеу немесе бақылау нысаны таңдалады. Статистикалық жиынтықтың көлемі айқындалады. Зерттеу жүргізу мерзімдері, мәліметтерді бақылау және жинаудың түрлері мен тәсілдері анықталады. Сосын, зерттеуді орындаушылар сипатталады. Техникалық жабдықтандыру мен қажетті материалдық құралдар сипатталады. Қаражат шығыны есептеледі. Белгілі бір кеңістікте және уақыт аралығында алынған, сан немесе сапалық белгілері бойынша біртекті нысандардың (элементтердің) тобын статистикалық жиынтық деп атайды. Ал оны құраушы нысандарды жиынтық бірліктері дейді. Статистикалық жиынтықтың әрбір элементін бақылау бірлігі дейді. Зерттелуге тиісті нысандардың жалпы жиынын (статистикалық жиынтықты) бас немесе жалпы жиынтық деп атайды. Бас жиынтықтағы бірліктер саны шекті де, шексіз де болуы мүмкін. Іс жүзінде, әдетте, бас жиынның кездейсоқ алынған бір бөлігі ғана зерттеледі. Егерде бас жиын шексіз (құраушы нысандар саны шексіз) немесе өте көп болса, онда зерттеу үшін алынған оның бөлігін таңдама немесе іріктелген жиынтық (таңдама) деп атайды. Статистикада бақылауға немесе өлшеуге болатын нысандардың немесе құбылыстардың қасиетін белгі деп атайды. Ол белгілердің мынадай түрлері бар: - атрибутивтік (сапалық, сөзбен анықталатын). Мысалы, жынысы, кәсібі, аурудың түрі, емдеу нәтижесі, тұратын жері, т.б. - сандық (сан арқылы анықталатын). Мысалы, бойдың ұзындығы, салмағы, емделу ұзақтығы, түрлі зерттеулердің сандық нәтижелері анықталады. - зерттелетін құбылысқа әсер ететін факторлық белгілер; - факторлық белгілер әсерінен өзгеретін нәтижелік белгілер. Мысалы: баланың жасына сәйкес бойы өседі (жасы – факторлық, ал бойы – нәтижелік белгі). Атрибутивтік белгілер бойынша жауаптарды топтау типологиялық, ал сандық белгілері бойынша топтау вариациялық деп аталады. Сапалық белгілер номинальды (категориальды) және реттік (ординальды) болып бөлінеді.Сандық белгілер дискретті (үзілісті) және үздіксіз деп бөлінеді. 3-нші мәліметтерді өңдеу кезеңінде мәліметтерді өңдеу бағдарламасы жасалады. Жиналған мәліметтерді тексеру, шифрлау, топтастыру жұмыстары, статистикалық кестелердің нұсқалары құрастырылады және толтырылады. Статистикалық көрсеткіштерді есептеу мен оларды графикалық әдістермен көрсету, алынған нәтижелерге статистикалық өңдеу жүргізіледі. 4-нші кезеңде мәліметтерді талдау және қорытындылау бағдарламасы жасалады. Ол бірнеше статистикалық әдістерден құралады, олар зерттелетін құбылыстың заңдылығын анықтайды. Статистикалық талдау жүргізгенде мынадай жұмыстар атқарылады: 1. Зерттеуді жүргізуде есептелген статистикалық көрсеткіштерге және олардың графикалық бейнелеуіне түсініктеме беру. Сонан кейін оларды оған ұқсас басқа зерттеулердің нәтижесімен салыстыру. 2. Жасалынған зерттеуді жазып, бейнелеу керек. 3. Қорытынды жасау. 4. Тәжірибеге енгізу үшін ұсыныстар қабылдау.  3-билет. Статистикалық зерттеулер нәтижесінің дұрыстығын бағалайтын статистикалық көрсеткіштер. 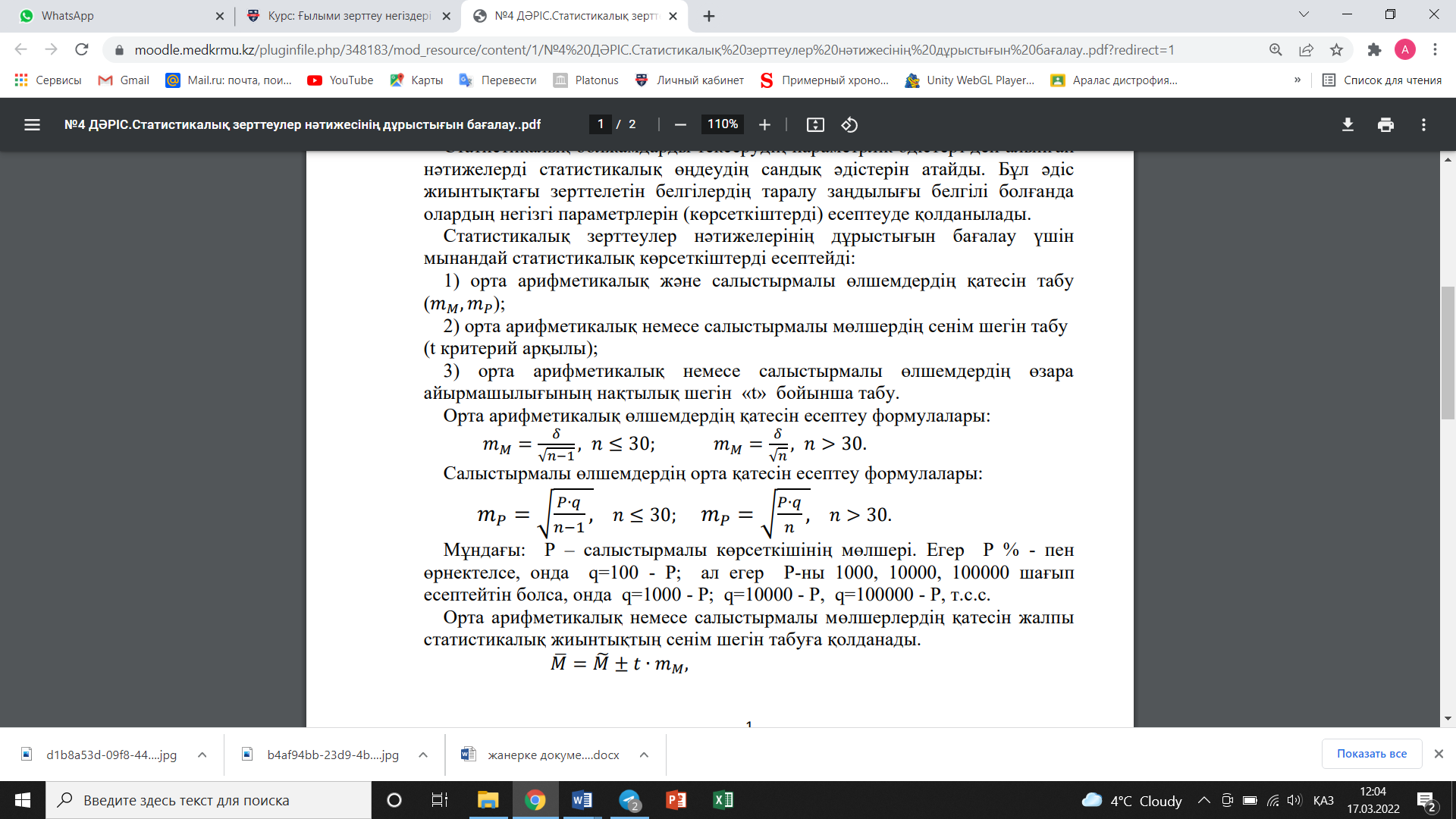 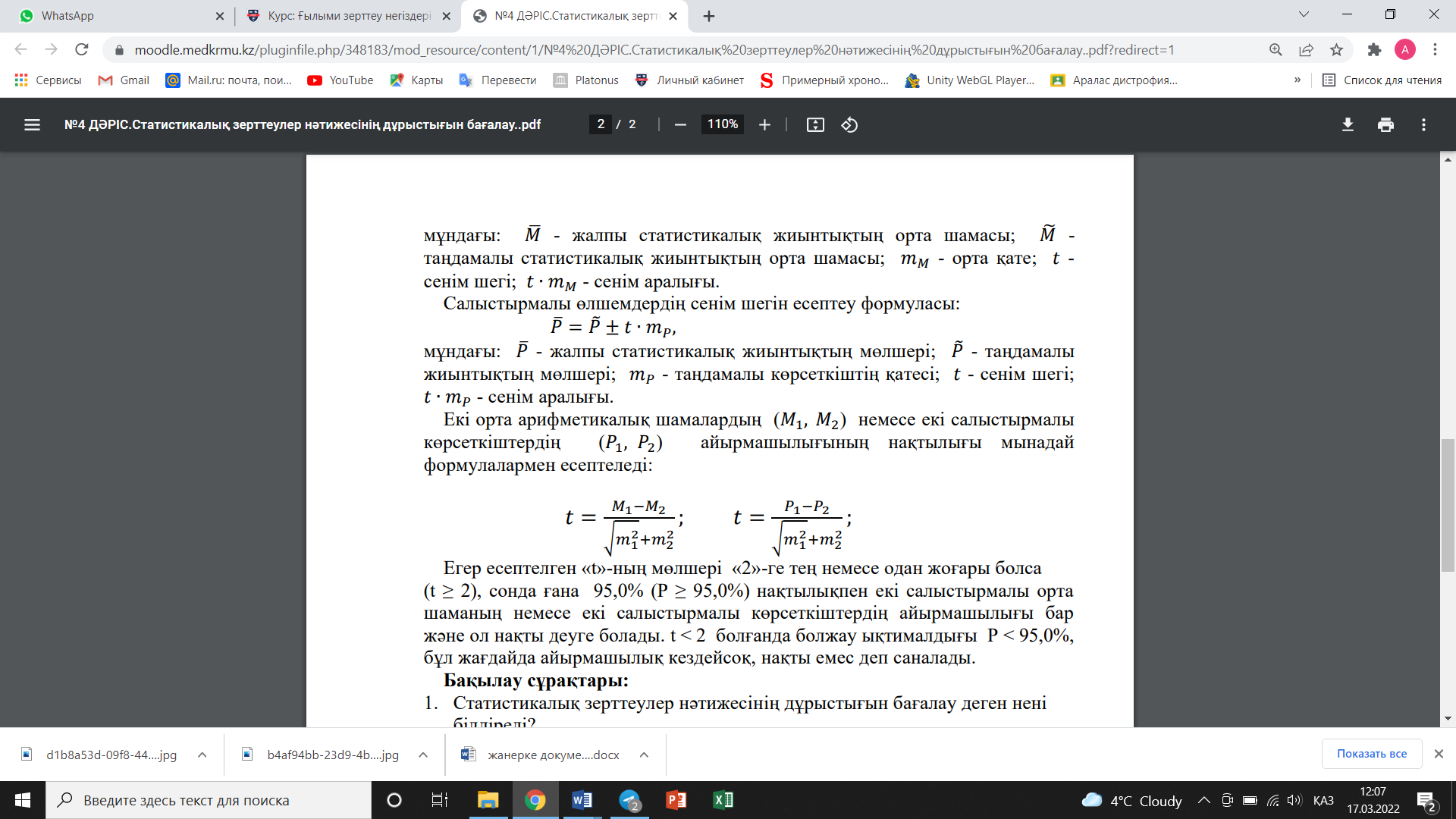  Билет. Статистикалық жиынтық, түрлері. Таңдамалық әдіс. Белгілі бір кеңістікте және уақыт аралығында алынған, сан немесе сапалық белгілері бойынша біртекті нысандардың (элементтердің) тобын статистикалық жиынтық деп атайды. Ал оны құраушы нысандарды жиынтық бірліктері дейді. Статистикалық жиынтықтың әрбір элементін бақылау бірлігі дейді. Зерттелуге тиісті нысандардың жалпы жиынын (статистикалық жиынтықты) бас немесе жалпы жиынтық деп атайды. Бас жиынтықтағы бірліктер саны шекті де, шексіз де болуы мүмкін. Іс жүзінде, әдетте, бас жиынның кездейсоқ алынған бір бөлігі ғана зерттеледі. Егерде бас жиын шексіз (құраушы нысандар саны шексіз) немесе өте көп болса, онда зерттеу үшін алынған оның бөлігін таңдама немесе іріктелген жиынтық (таңдама) деп атайды. 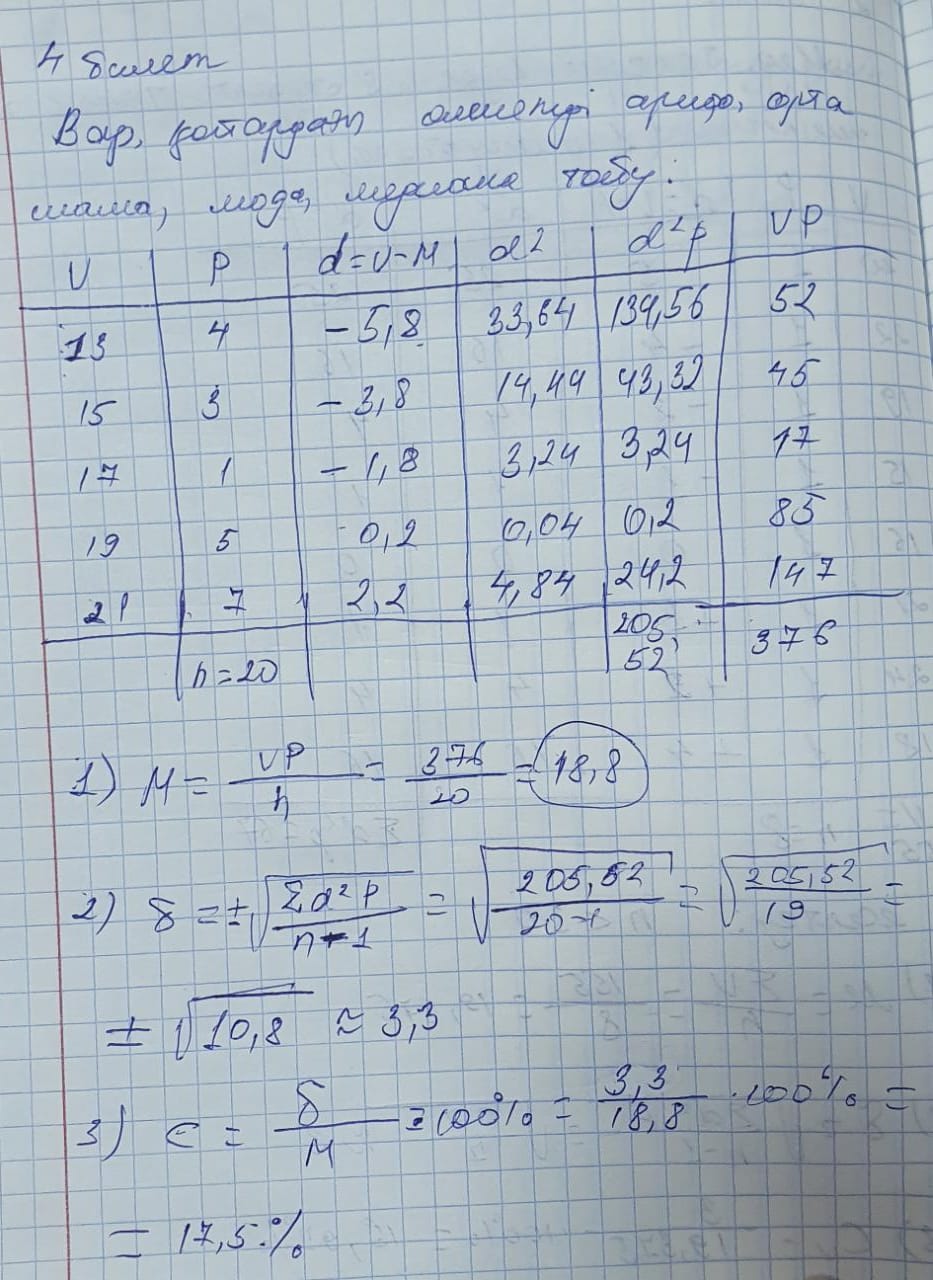 5 – билет. Статистикалық мәліметтерді жинау кезеңінде жүргізілетін жұмыстар. Бақылау бірлігі, оның тіркелінетін белгілерінің классификациясы. - Зерттеу бағдарламасын жасағанда барлық анықтайтын сұрақтарды белгілейді және мәліметтерді өңдеу жолдары мен талдау тәсілдері көрсетіледі. Статистикалық зерттеудің 2-нші кезеңінде бақылау бірлігі анықталады және мәліметтерді жинаудың бағдарламасы жасалады. Мәліметтерді жинау бағдарламасына есепке алу немесе бақылау белгілері кіреді. Есепке алынатын белгілер сұрақ ретінде тіркеу құжаттарында болады. Анкета, сұрақ-жауап қағаздары, карталар қолданылады. 3-нші мәліметтерді өңдеу кезеңінде мәліметтерді өңдеу бағдарламасы жасалады. Жиналған мәліметтерді тексеру, шифрлау, топтастыру жұмыстары, статистикалық кестелердің нұсқалары құрастырылады және толтырылады. Статистикалық көрсеткіштерді есептеу мен оларды графикалық әдістермен көрсету, алынған нәтижелерге статистикалық өңдеу жүргізіледі. Статистикалық кестелерге қойылатын талаптар. Кестелердің аталуы анық және қысқа, мазмұнына сәйкес болуы керек. Кестеде бастауыш пен баяндауышты ажырату керек. Статистикалық бастауыш дегеніміз талданатын негізгі белгі. Статистикалық баяндауыш (біреу немесе бірнешеу) дегеніміз бастауышты сипаттайтын белгілер, яғни есепке алынатын белгілер. Бастауыш кестенің сол жағынан тігінен, ал баяндауыштар көлденеңінен жазылады. Статистикалық кестелердің түрлері: жай (қарапайым); топтастық; комбинацияланған. Жай статистикалық кестеде бір ғана статистикалық бастауыш болады, барлық мәліметтер бір белгімен алынады. Топтастық статистикалық кестеде бір бастауыш және онымен байланысқан бірнеше баяндауыштар болады. Комбинацияланған (аралас) статистикалық кестеде бастауышпен байланысқан және өзара бір-бірімен байланысқан баяндауыштар болады. 4-нші кезеңде мәліметтерді талдау және қорытындылау бағдарламасы жасалады.  6 – билет. Статистикалық мәліметтерді өңдеу кезеңінде жүргізілетін жұмыстар. Статистикалық кестелер, құрамы, түрлері. 3-нші мәліметтерді өңдеу кезеңінде мәліметтерді өңдеу бағдарламасы жасалады. Жиналған мәліметтерді тексеру, шифрлау, топтастыру жұмыстары, статистикалық кестелердің нұсқалары құрастырылады және толтырылады. Статистикалық көрсеткіштерді есептеу мен оларды графикалық әдістермен көрсету, алынған нәтижелерге статистикалық өңдеу жүргізіледі. Статистикалық кестелерге қойылатын талаптар. Кестелердің аталуы анық және қысқа, мазмұнына сәйкес болуы керек. Кестеде бастауыш пен баяндауышты ажырату керек. Статистикалық бастауыш дегеніміз талданатын негізгі белгі. Статистикалық баяндауыш (біреу немесе бірнешеу) дегеніміз бастауышты сипаттайтын белгілер, яғни есепке алынатын белгілер. Бастауыш кестенің сол жағынан тігінен, ал баяндауыштар көлденеңінен жазылады. Статистикалық кестелердің түрлері: жай (қарапайым); топтастық; комбинацияланған. Жай статистикалық кестеде бір ғана статистикалық бастауыш болады, барлық мәліметтер бір белгімен алынады. Топтастық статистикалық кестеде бір бастауыш және онымен байланысқан бірнеше баяндауыштар болады. Комбинацияланған (аралас) статистикалық кестеде бастауышпен байланысқан және өзара бір-бірімен байланысқан баяндауыштар болады.  7 – билет. Статистикалық мәліметтерді талдау кезеңінде жүргізілетін жұмыстар. Статистикалық талдауда кездесетін қателер. 4-нші кезеңде мәліметтерді талдау және қорытындылау бағдарламасы жасалады. Ол бірнеше статистикалық әдістерден құралады, олар зерттелетін құбылыстың заңдылығын анықтайды. Статистикалық талдау жүргізгенде мынадай жұмыстар атқарылады: 1. Зерттеуді жүргізуде есептелген статистикалық көрсеткіштерге және олардың графикалық бейнелеуіне түсініктеме беру. Сонан кейін оларды оған ұқсас басқа зерттеулердің нәтижесімен салыстыру. 2. Жасалынған зерттеуді жазып, бейнелеу керек. 3. Қорытынды жасау. 4. Тәжірибеге енгізу үшін ұсыныстар қабылдау. Статистикалық талдауда жиі кездесетін қателер: - Зерттеуді жүргізу кезеңіндегі қателер. - Статистикалық көрсеткіштерді дұрыс пайдаланбау. - Статистикалық талдаудың логикалық қателері.  8 – билет . Салыстырмалы өлшемдер, түрлері, графикалық бейнелеулері. Статистикалық жиынтықтың құрамындағы белгілерді немесе құбылыстарды зерттеуде және оларды сипаттауда статистикалық өлшемдерді пайдаланады. Статистикалық өлшемдердің екі түрі бар: абсолюттік және салыстырмалы. Дәрігер күнделікті іс-әрекетінде кез келген ақпаратты абсолют сандармен алады. Абсолюттік мөлшер бір жиынтықтың көлемін немесе жалпы санын көрсетеді. Мысалы: халық саны, аурулардың саны, мекемелердің саны, дәрігерлердің саны және т.б. Қоғамдық денсаулық және денсаулық сақтау мекемелерінің іс-әрекетінде, медицина қызметкерінің іс-әрекетінде терең талдау жүргізу үшін салыстырмалы өлшемдер деп аталатын жалпылама көрсеткіштер қолданылады. Салыстырмалы өлшемдер статистикалық жиынтықтардың бір-бірімен байланысын тауып, салыстыруда қолданылады. Олар екі абсолюттік өлшемдерді салыстыру, бөлу және сол бөлшекті 100, 1000, 10000, 100000-ға көбейту арқылы табылады. Сондықтан, салыстырмалы өлшемдерді пайызбен, промиллимен, продецемиллимен, просантимиллимен, т.б. белгілейді. Салыстырмалы өлшемдерді есептегеннен кейін оларға графикалық бейнелеу жасалады. Оның негізгі мақсаты – статистикалық көрсеткіштерді көрнекті етіп көрсету және талдауды жеңілдету. Графикалық бейнелеудің бірнеше түрі бар: 1. Диаграммалар – сызықты, тарамдалған, бағаналы, ішкі бағаналы, секторлы, көлемді, суреттік (фигуралық). 2. Картограммалар. 3. Картодиаграммалар. Салыстырмалы өлшемдерді графикалық бейнелеуде мынандай ережелер сақталуы тиіс: - әрбір графикалық бейнелеудің аты, мазмұны, уақыты және орны көрсетіледі; - графикалық бейнелеу белгілі масштабпен жасалады; - әрбір графикалық бейнелеуге түсініктеме беріледі; - графикалық бейнелеудің түрі бейнеленетін көрсеткіштің мәніне сәйкес болуы.  9 – билет. Вариациялық қатар, түрлері. Вариация коэффициенті, есептелуі, қолданылуы. Вариациялық қатар – зерттелетін белгінің сандық мөлшерлерін жоғарылату немесе төмендету ретімен орналастыру. Вариациялық қатар статистикалық жиынтық белгілерінің сан түріндегі мәнін көрсетеді және орта шаманы есептегенде қолданылады. Вариациялық қатардың негізгі белгілеулері: - V – варианта – зерттелетін белгінің сандық мәні; - p – жиілік – әр вариантаның кездесу жиілігі; - n – жалпы бақылау саны – барлық жиіліктің қосындысы, 𝑛 = ∑ 𝑝; - 𝑉𝑚𝑎𝑥, 𝑉𝑚𝑖𝑛 – вариациялық қатарды шектейтін шеткі варианталар (қатардың шектері); - A – қатар амплитудасы, яғни ең жоғарғы және ең төменгі варианталардың айырмасы - 𝐴 = 𝑉𝑚𝑎𝑥 − 𝑉𝑚𝑖𝑛. Вариациялық қатардың түрлері: қарапайым және топтастырылған. Қарапайым түрінде әрбір варианта бөлек (бір рет) беріледі; ал топтастырылған түрінде бірнеше сандық маңызы бірдей варианталар бір топқа топтастырылып, топқа кіргізілген варианталардың бәрінің жиілігі қосылады. Топтастырылған вариациялық қатарды құру тәртібі: 1) қатардағы топ санын белгілеу, мысалы мына кестедегідей тәртіп қолданылады: 1) Топ аралығын есептеу: 𝑖 = (𝑉𝑚𝑎𝑥 − 𝑉𝑚𝑖𝑛): топ саны. 2) Әр топ ортасын және шегін табу. 3) Зерттелетін жиынтықты топқа бөлу; 4) Вариациялық қатарды графиктік сызумен бейнелеу. Вариациялық қатар құрылғаннан кейін орта шаманы есептейді. 𝑪𝑽- вариациялық коэффициент (көрсеткіш) – вариациялық қатардың ауытқуының салыстырмалы өлшемі. Есептеу формуласы: 𝑪𝑽 = 𝜹 𝑴 ∙ 𝟏𝟎𝟎%, мұндағы δ - орта квадраттық ауытқу, 𝑀 – орта арифметикалық орта. 3 Белгінің мөлшерлерінің айырмашылығын жобамен бағалау үшін бұл коэффициенттің мынадай деңгейлері бар: 1) 𝐶𝑉20% - өте жоғары айырмашылық.  10 – билет. Статистикалық болжам, нөлдік және балама болжамдар ұғымдары. Статистикалық болжамдарды тексеру әдістемесі. Статистикалық жорамал (болжам) – бұл таңдама көрсеткіштерінің негізінде тексеру болатын бас жиынтықтың таралу түрі жөніндегі немесе белгісіз параметрлерінің шамасы жөніндегі ұйғарым. Түрі белгілі таралудың параметрлері жөніндегі статистикалық жорамалдар параметрлік жорамалдар, ал белгісіз таралудың түрі жөніндегі жорамалдар параметрлік емес жорамалдар деп аталады. Статистикалық жорамалдар таңдама деректері негізінде статистикалық әдістермен тексеріледі. Жорамалдарды статистикалық тексеруге әртүрлі үрдістерді салыстыру және бағалау жатады: емдеудің тиімділігі, ауырудың және одан жазылу кезеңдерінің ұзақтығы, сырқаттың ауырлығы, емдеу әдістері. Тексерілуге жататын негізгі жорамал нөлдік жорамал деп аталады және Н0 арқылы белгіленеді. Нөлдік жорамалмен бәсекелес, яғни оған қарама-қайшы келетін жорамал балама жорамал деп аталады және Н1 арқылы белгіленеді. Бір ғана ұйғарымнан тұратын жорамал жай, ал жай жорамалдардың шекті немесе шексіз санынан тұратын жорамал күрделі деп аталады. Мысалы, Н0: а=а0 - жай, Н0: а>5 - күрделі. Н0 жорамалын қабылдау немесе жоққа шығару жөніндегі ереже статистикалық критерий деп аталады.  11 – билет. Статистикалық болжамдарды тексерудегі мәнділік деңгейі, 1-нші және 2-нші текті қателер. Жорамалдарды тексерудің негізгі қағидасы: Tn критерий статистикасының мүмкін мәндер жиыны екі қиылыспайтын ішкі жиындарға бөлінеді: 1) S сыни аймағы, яғни Н0 жорамалын жоққа шығару аймағы, 2) жорамалды қабылдау аймағы. Егер критерий статистикалық бақылау нәтижелері бойынша есептелген мәндері (Tбақ=T(X1,X2,…,Xn )) S сыни аймағына түссе, онда Н0 жоққа шығарылады және Н1 қабылданады, ал егер Тбақ S аймағына түссе, онда Н0 қабылданады, ал Н1 жоққа шығарылады. Статистикалық жорамалдарды қабылдау немесе жоққа шығару туралы шешім таңдама деректері бойынша қабылданады. Сондықтан, шешімнің қате болу мүмкіндігімен санасу қажет. Қателік екі текті болуы мүмкін. Бірінші текті қателік - Н0 жоққа шығару, негізінде ол дұрыс. Екінші текті қателік - Н0 қабылдау, негізінде ол дұрыс емес. Бірінші текті қателікті жіберу ықтималдығы критерийдің мәнділік деңгейі деп аталады және (альфа) арқылы белгіленеді. Екінші текті қателікті жібермеу ықтималдығы критерийдің қуаттылығы деп аталады және (бета) арқылы белгіленеді.   12 – билет. Орта арифметикалық қате, салыстырмалы мөлшердің қатесі, есептелуі, қолданылуы. Статистикалық зерттеулер нәтижелерінің дұрыстығын бағалау үшін мынандай статистикалық көрсеткіштерді есептейді: орта арифметикалық және салыстырмалы өлшемдердің қатесін табу (𝑚𝑀, 𝑚𝑃); 2) орта арифметикалық немесе салыстырмалы мөлшердің сенім шегін табу (t критерий арқылы); 3) орта арифметикалық немесе салыстырмалы өлшемдердің өзара айырмашылығының нақтылық шегін «t» бойынша табу.   13 - билет. Орта арифметикалық шамалар, түрлері, есептеу әдістері. Мода мен медиана. Орта шама – құбылыстың біртектес жиынтығының нақты белгісі бойынша қорытылған сипаттамасы. Орташа шаманың мәні: жиынтықтың бір белгі сипаттамасының барлығына тән және жалпы; орта шамаларда кездейсоқ жағдайлармен өзара байланыстағы жиынтық бірліктерінің жеке әртүрлілігі жойылады; кез-келген бір белгі бойынша әртүрлі жиынтықты салыстыруға орташа шама мүмкіндік береді. Бірақ орта шамаларды қолданғанда зерттелген статистикалық жиынтықтың бірыңғай болуын 2 қадағалау керек. Мысалы, ер балалар мен қыздардың бойын, салмағын және т.б. сандық белгілерді сипаттағанда. Орта шамалар медицинада және денсаулық сақтау саласында өте жиі қолданылады: дене өсуін сипаттауда; адамның ағзаларының физиологиялық шамасын бағалауда; санитарлықэпидемиологиялық мөлшерді, нормативтік молшерлерді белгілеуде; денсаулық сақтау мекемелерінің жұмысын сипаттауда т.б. жағдайларда. Вариациялық қатар орта шаманы табу үшін және статистикалық жиынтық белгісі мөлшерінің әртүрлілігін сипаттау үшін (𝛿,𝐶𝑉)қолданылады. Орта шаманың түрлері: 𝑀0 - мода – жиынтық белгісінің ең жиі кездесетін мөлшері; 𝑀𝑒 - медиана – вариациялық қатардың тең ортасында тұрған мөлшер. M - орта арифметикалық шаманың екі түрі бар: жай арифметикалық орта шама және өлшемді арифметикалық орта шама. Жай арифметикалық орта шама әр вариантаның біркелкі жиілікпен кездесуінде және бақылау санының қосындысы n ≤ 30 болғанда қолданылады. Есептеу формуласы: 𝑴 = ∑ 𝑽/𝒏 . Өлшемді арифметикалық орта шама әр вариантаның жиілігі біркелкі болмай кездескен жағдайда және бақылау санының қосындысы көп (n > 30) болғанда қолданылады. Есептеу формуласы: 𝑴 = ∑ 𝑽𝑷/𝒏 .  14 – билет. Вариациялық қатардағы белгінің айырмашылықтарын анықтау үшін қолданылатын өлшемдер.   15 – билет . Бас статистикалық жиынтық құрамындағы орта және салыстырмалы шамалардың сенім шегі, сенімділік аралығы 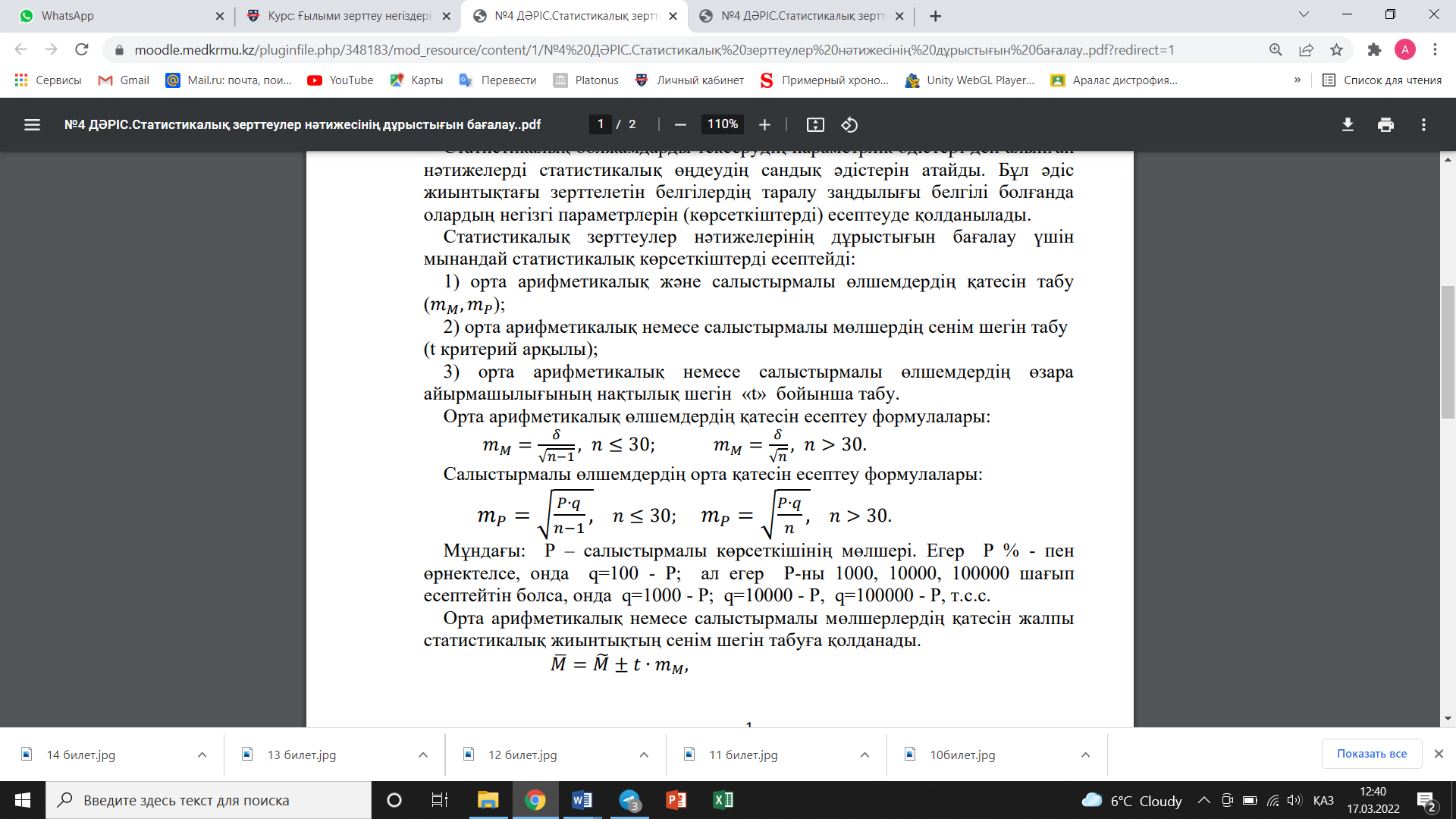   16 – билет . Статистикалық болжамдарды тексерудің параметрлік әдісі. Статистикалық болжамдарды тексерудің параметрлік әдістері деп алынған нәтижелерді статистикалық өңдеудің сандық әдістерін атайды. Бұл әдіс жиынтықтағы зерттелетін белгілердің таралу заңдылығы белгілі болғанда олардың негізгі параметрлерін (көрсеткіштерді) есептеуде қолданылады. Статистикалық зерттеулер нәтижелерінің дұрыстығын бағалау үшін мынандай статистикалық көрсеткіштерді есептейді: орта арифметикалық және салыстырмалы өлшемдердің қатесін табу (𝑚𝑀, 𝑚𝑃); 2) орта арифметикалық немесе салыстырмалы мөлшердің сенім шегін табу (t критерий арқылы); 3) орта арифметикалық немесе салыстырмалы өлшемдердің өзара айырмашылығының нақтылық шегін «t» бойынша табу. Орта арифметикалық өлшемдердің қатесін есептеу формулалары: 𝑚𝑀 = 𝛿 /√𝑛−1 , 𝑛 ≤ 30; 𝑚𝑀 = 𝛿/ √𝑛 , 𝑛 > 30.  17 – билет. Статистикалық болжамдарды тексерудің параметрлік емес әдістері. Параметрлік емес критерийлер бас жиынтықтың таралу түріне тәуелсіз, берілген жиынтықтың варианталары мен олардың жиіліктеріне ғана тәуелді функциялар болып табылады. Параметрлік емес критерийлер параметрлік критерийлер үшін қажетті болып табылатын таралудың кейбір параметрлерін есептеуді талап етпейді. Сондықтан параметрлік емес критерийлерді және S параметрлік емес статистика әдістерін параметрден бос немесе еркін таралған деп атайды. Параметрлік емес критерийлерді қолданудың тиімділігі мен мүмкіндіктері: - зерттелетін жиынтықтың таралу түрі белгісіз, бұл көбіне көлемі аз жиынтықтармен жұмыс істегенде мәнді; - сандық және сапалық белгілермен жұмыс істеуге мүмкіндік береді; - таңдама орта және таңдама ортаның стандартты қатесін есептеу талап етілмейді; - зерттеліп отырған жиынтықтар арасында айырмашылықтардың бар немесе жоқ екендігін анықтауға, егер бар болса олардың кездейсоқ немесе заңдылық екендігін тағайындауға мүмкіндік береді; - зерттелетін құбылыстар немесе белгілер арасындағы байланысты немесе тәуелділікті анықтауға мүмкіндік береді; Параметрлік критерийлердің параметрлік емес аналогтары бар. Стьюденттің жұптаспаған критерийі үшін параметрлік емес Манна-Уитни, жұптасқан критерийі үшін параметрлік емес Уилкоксон критерийлері аналогтары болып табылады. Манн-Уитни критерийі байланыспаған таңдамалардың n1, n2  18 – билет. Орта квадраттық ауытқу, есептелуі, қолданылуы.   19 – билет. Колмогоров-Смирновтың келісім критерийі. Колмогоров-Смирновтың келісім критерийі мәндердің аз санында да жеткілікті сезімтал болып келеді. Оны кез-келген таралудың сәйкестігін тексеру үшін қолдануға болады. Алайда, жорамал бойынша тағайындалған таралу функциясы үздіксіз болуы керек екендігін ескеру қажет. Параметрлік емес критерийлер бас жиынтықтың таралу түріне тәуелсіз, берілген жиынтықтың варианталары мен олардың жиіліктеріне ғана тәуелді функциялар болып табылады. Параметрлік емес критерийлер параметрлік критерийлер үшін қажетті болып табылатын таралудың кейбір параметрлерін есептеуді талап етпейді. Сондықтан параметрлік емес критерийлерді және S параметрлік емес статистика әдістерін параметрден бос немесе еркін таралған деп атайды.  20 – билет . Пирсонның Хи-квадрат келісім критерийі. Пирсонның Хи-квадрат келісім критерийі таралудың заңы жөніндегі жай жорамалды тексеру үшін ең жиі қолданылатын критерий. Тексеру үшін нөлдік жорамалды ұйғарады Н0: “эмпирикалық таралу мен теориялық таралудың арасында ешқандай айырмашылық жоқ”. Критерийді қолданудың негізгі идеясы теориялық жиіліктер мен эмпирикалық жиіліктерді салыстыру болып табылады. Егер эмпирикалық жиіліктер (ni) теориялық жиіліктерден (npi) қатты ерекшеленетін болса, онда тексерілетін жорамалды жоққа шығару керек; керісінше жағдайда қабылдау қажет.   21 – билет . Статистикалық жиынтықтағы белгінің қалыпты таралуы. Гаусс қисығы. Қалыпты (Гаусстық) таралу Таралуы олардың басқа түрлеріне қарағанда жиірек кездесетін және статистикадағы ең маңызды таралулардың бірі - қалыпты таралу. Қалыпты таралу түрінде варианталар вариациялық қатардың ортасына қарасты симметриялы түрде орналасады және олардың саны орталықтан алыстаған сайын біртіндеп кеміп отырады, сонымен бірге бақылаудың ең көп саны қатардың ортасына жинақталады. Кездейсоқ шамалардың мұндай таралу түрі медициналық-биологиялық көрсеткіштерде жиірек кездесетін болғандықтан, оны «қалыпты» деп атаған. Гаусс қисығы - Қалыпты таралудың графигі орта мәнге қатысты симметриялы, қоңырау тәрізді болады және қалыпты таралу қисығы немесе Гаусс қисығы деп аталады. Қалыпты таралудың негізгі сипаттамалары: толығымен екі параметрмен анықталады: орта мән және дисперсия; қоңырау тәріздес(унимодальды); орта мәнге қатысты симметриялы; егер орта мән ұлғайса оңға қарай, орта мән азайса солға қарай жылжиды(дисперсия түрақты жағдайда); қисықтың түрі бас жиынтықтың стандарттық ауытқуымен анықталады; стандарттық ауытқуы аз таралуға жіңішке, жоғары созылған қисықтар, ал стандарттық ауыткуы үлкен таралуға жазыңқы қисықтар сәйкес келеді.  22 – билет. Корреляциялық талдау. Пирсон әдісі. Корреляциялық байланысты бейнелеу тәсілдері: кестелік, графикалық (шашырау диаграммасы), корреляция коэффициенті. Егер нәтижелік белгінің бір факторға байланысын қарастырса, оны парлық корреляция дейді де, ал екі немесе бірнеше факторға байланысын қарастырса, оны көп өлшемді корреляция дейді. Корреляциялық талдау жасау корреляциялық кесте мәліметтеріне сүйенеді. Мұндай кестелер екі түрде болады. Бірінде ол кесте мәліметтерді санау арқылы жасалса, екіншісінде қарапайым корреляциялық кесте, корреляциялық тор немесе корреляциялық матрица күйінде болады. Ал, графикалық тәсілдің мақсаты – корреляциялық өріс құру. Корреляциялық байланыс бағыты бойынша: тікелей, кері болып бөлінеді. Квадраттар әдісі (Пирсон әдісі). Корреляция коэффициентін Пирсон әдісі бойынша есептеу формуласы: 𝑟𝑥𝑦 = ∑(𝑑𝑥∙𝑑𝑦)/√(∑(𝑑𝑥 2 ∙ 𝑑𝑦 2 ) , мұндағы: 𝑟𝑥𝑦 – корреляциялық коэффициент; x және y – өзара байланысы анықталатын белгілер; 𝑑𝑥 және 𝑑𝑦 - әрбір ауыспалы вариантаның өзінің орта арифметикалық өлшемінен ауытқуы (𝑀𝑥 және 𝑀𝑦). 𝑑𝑥 = 𝑥 − 𝑀𝑥; 𝑑𝑦 = 𝑦 − 𝑀𝑦. Есептелген нәтиже 0 мен 1 арасында (+) немесе (-) белгімен болуы мүмкін. Ол байланыстың бағыты мен күшін көрсетеді.  23 – билет. Корреляциялық талдау. Спирмен әдісі. Корреляциялық байланысты бейнелеу тәсілдері: кестелік, графикалық (шашырау диаграммасы), корреляция коэффициенті. Егер нәтижелік белгінің бір факторға байланысын қарастырса, оны парлық корреляция дейді де, ал екі немесе бірнеше факторға байланысын қарастырса, оны көп өлшемді корреляция дейді. Корреляциялық талдау жасау корреляциялық кесте мәліметтеріне сүйенеді. Мұндай кестелер екі түрде болады. Бірінде ол кесте мәліметтерді санау арқылы жасалса, екіншісінде қарапайым корреляциялық кесте, корреляциялық тор немесе корреляциялық матрица күйінде болады. Ал, графикалық тәсілдің мақсаты – корреляциялық өріс құру. Корреляциялық байланыс бағыты бойынша: тікелей, кері болып бөлінеді. Рангілік әдісті қолдану жөніндегі нұсқаулар: 1) егер байланыс күшінің деңгейін нақты түрде білу қажет болмаса, ондай мәліметтерді болжамдап алуға болады (яғни, дәл сандық өлшеммен анықталмайтын құбылыстар арасындағы байланысты ашу немесе оны бағалау қажет болғанда). 2) егер белгілер (n≤ 30) сандық және сапалық (атрибутивтік) белгілер болса; 3) белгілердің үлестірім қатары ашық варианталар болса (мысалы, жұмыс өтілі 1 жылға дейін). Рангілік әдіс. Корреляция коэффициентін Спирмен әдісі бойынша есептеу формуласы: 𝜌𝑥𝑦 = 1 – 6/∑ 𝑑 2 𝑛∙(𝑛2−1) , мұндағы: 𝜌𝑥𝑦 – рангілі корреляция коэффициенті; d – рангтардың айырмашылығының ауытқуы: d=x-y; n–бақылау саны. Есептелген нәтиже 0 мен 1 арасында (+) немесе (-) белгімен болуы мүмкін. Ол байланыстың бағыты мен күшін көрсетеді. Корреляция коэффициенті +1,0 немесе - 1,0 болса, оны толық (функционалдық) байланыс дейді.  24 – билет. Регрессиялық талдау, регрессия коэффициенті, қолданылуы. Екі айнымалы шаманың бір-бірімен байланысының бағыты мен күші корреляциялық көрсеткіш арқылы анықталады. Ал, бір белгі мөлшерінің екінші белгінің мөлшері өзгергенде сан жағынан қаншалықты өзгеретіні регрессия әдісі арқылы анықталады. Регрессия – бір-бірімен байланысты белгілердің бірінің шамасы белгілі болса, екіншісінің орта шамасын табуға мүмкіншілік беретін әдіс. Мысалы, 1 сынып оқушыларының бойы 1 см-ге ұзарса салмағы қаншалықты өзгеретінін регрессиялық талдау арқылы анықтайды. Көбінесе, регрессиялық әдіс физикалық дамудың нормативті шкалалары мен стандарттарын жасау үшін қолданылады. Осы мақсатта регрессия коэффициенті және басқа да параметрлер қолданылады. Регрессия коэффициенті – абсолюттік шама, ол бір белгінің мөлшері бірлік санға өзгергенде екінші белгінің өлшемі қаншалықты өзгеретінін көрсетеді. Регрессия коэффициентін есептеу формуласы: 𝑅𝑦⁄𝑥 = 𝑟𝑥𝑦 ∙ 𝛿𝑦 𝛿𝑥 . Мұндағы, 𝑅𝑦⁄𝑥 - регрессия коэффициенті, 𝑟𝑥𝑦 - корреляция коэффициенті, 𝛿𝑥 және 𝛿𝑦 - X және Y қатарларының орта квадраттық ауытқулары.  25 – билет. Сызықты регрессиялық талдау, теңдеуі, параметрлері. Регрессия коэффициенті арқылы бір белгінің (мысалы, салмақтың) мөлшерін арнайы өлшеу жүргізбей-ақ, екінші белгінің (мысалы, бойдың) орта шамасы бойынша табуға болады. Ол үшін сызықты регрессия теңдеуін қолданады: 𝑦 = 𝑀𝑦 + 𝑅𝑦⁄𝑥 (𝑥 − 𝑀𝑥 ). Мұндағы, 𝑦 - ізделіп отырған белгінің (салмақтың)шамасы; 𝑥 - бірінші белгінің (бойдың) шамасы; 𝑅𝑦⁄𝑥 – салмақты бойға салыстырғандағы регрессия коэффициенті; 𝑀𝑦 (белгілі жасқа тән салмақтың орта шамасы), 𝑀𝑥 (бойдың орта шамасы) – 𝑦 және 𝑥 белгілерінің белгілі орта шамалары. Мысал: 9 жасар қыздардың орта есеппен салмағы 𝑀𝑦= 30,3 кг., бойының ұзындығы орта есеппен 𝑀𝑥= 135,5 см. Егер 9 жасар қыздардың орта есеппен бойының ұзындығы: 𝑥 = 132 см болса, онда салмағының орта шамасы қандай болатынын табуға болады: 𝑦 = 𝑀𝑦 + 𝑅𝑦⁄𝑥 (𝑥 − 𝑀𝑥 ) = 30,3 + 0,43 (132 – 135,5) = 28,8 кг. Сонымен, қорытынды: орта есеппен 9 жасар қыздардың бойының ұзындығы 132 см болса, бұған сәйкес салмақтың мөлшері орта шамамен 28,8 кг болады. Бұл теңдеу екі белгінің арасында түзу сызықты байланыс болғанда қолданылады. Регрессия теңдеуінің графигі – регрессия сызығы. Жеке адамдардың белгілерінің мөлшері әртүрлі. Мысалы, бойларының ұзындығы бірдей болғанымен табылған салмаққа тән өзгерушіліктің шамасын анықтау үшін регрессия коэффициентінің ауытқуы қолданылады. Регрессияның орта квадраттық ауытқуы нәтижелік белгінің (y) өлшемінің әртүрлі болуына сипаттама береді. Ол мына формуламен есептеледі: 𝛿𝑅𝑦⁄𝑥 = 𝛿𝑦 ∙ √1 − 𝑟𝑥𝑦 2 . Мұндағы, 𝛿𝑅𝑦⁄𝑥 - сигма (орта квадраттық ауытқу); 𝛿𝑦 - y-зерттелінетін белгінің (мысалы, салмақтың) орта квадраттық ауытқуы; 𝑟𝑥𝑦 - x және y белгілері арасындағы корреляция коэффициенті. Неғұрлым 𝛿𝑅𝑦⁄𝑥 - тың мөлшері аз болса, соғұрлым әр адамның зерттелген белгісінің орта шамасынан айырмашылығы аз болады. 𝛿𝑦= ± 4,2; 𝑟𝑥𝑦= +0,6; 𝛿𝑅𝑦⁄𝑥 = 𝛿𝑦 ∙ √1 − 𝑟𝑥𝑦 2 = 4,2 ∙ √1 − 0,6 2 = +3,36 кг. Регрессия теңдеуін және регрессия ауытқуын пайдаланып регрессия коэффициенті арқылы регрессия шкаласын құрады. Бұл шкала бойынша балалардың және жас өспірімдердің дене дамуын зерттегенде бойдың, салмақтың, кеуде көлемінің мөлшерінің жасына сәйкестігін бағалайды. Бұнда, егер бала денесінің салмағы нақты бір бой ұзындығы бойынша регрессияның 1 сигмасы шегінде: 𝑦 ± 1𝜎𝑅𝑦⁄𝑥 болса, онда физикалық даму салмақ бойынша гармониялы деп саналады. Ал, егер 𝑦 ± 2𝜎𝑅𝑦⁄𝑥 болса, онда физикалық даму дисгармониялы деп; 𝑦 ± 3𝜎𝑅𝑦⁄𝑥 болса, қатты дисгармониялы деп есептеледі (яғни, салмағы өте артық немесе өте кем). Бұл регрессиялық әдіс дәрігерлердің күнделікті жұмысында да қолданылады. Регрессия шкаласы бойынша қан қысымының ең жоғарғы деңгейі белгілі болса, оған сәйкес ең төменгі деңгейін табуға болады.  |

