Прил 2. Бюджетное ограничение потребителя. Задачи для самостоятельного решения
 Скачать 212.87 Kb. Скачать 212.87 Kb.
|
|
Задачи: (ЧФ, 2, с. 304). Производственная функция фирмы-монополиста имеет вид 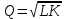 , а функция спроса на продукт: , а функция спроса на продукт: 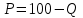 . Цена труда, w, равна 4 у. е. в час, цена капитала, r, равна 1 у. е. в час. . Цена труда, w, равна 4 у. е. в час, цена капитала, r, равна 1 у. е. в час.а) Определите объем выпуска, максимизирующий прибыль фирмы. б) Найдите оптимальное количество используемых факторов производства. в) Выведите косвенную функцию прибыли и предложения продукта для данной фирмы, функции спроса на ресурсы. г) Рассчитайте величину получаемой монополистом прибыли, ренты, чистых потерь экономики. основанную на ценности предельного продукта их труда. Пусть технология фирмы описывается функцией 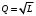 , цена продукта на совершенно конкурентном рынке 64 предложение труда – функцией , цена продукта на совершенно конкурентном рынке 64 предложение труда – функцией б) Найдите равновесие фирмы, определите величину экономической ренты фирмы и работников, величину эксплуатации труда. Чистые потери благосостояния от монополизации рынка труда; в) Определите последствия установления минимальной заработной платы на уровне 10; г) Определите последствия установления минимальной заработной платы на уровне 20; д) При каком уровне заработной платы фактически максимизируется общественное благосостояние. 3. Пусть технология фирмы описывается функцией Рассчитайте благосостояние экономики в следующих случаях: А) Фирма – совершенный конкурент на рынке труда, монополист на рынке продукта Б) Фирма - совершенный конкурент на продуктовом рынке, монопсонист на рынке труда. Фиаско рынка Задачи. (ЧФ, 1, с. 356). Производство товара Х в конкурентной отрасли сопровождается отрицательным внешним эффектом – загрязнением окружающей среды. Предельные издержки загрязнения (MEC) описываются функцией 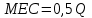 , совокупные предельные издержки отрасли (PMC) – функцией , совокупные предельные издержки отрасли (PMC) – функцией 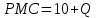 и отраслевой спрос – функцией и отраслевой спрос – функцией 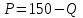 а) Определите объем выпуска и цену в отрасли в отсутствие корректирующих мер. б) Определите общественно эффективный объем выпуска и потери общества из-за загрязнения. в) Какой потоварный налог следует установить, чтобы побудить фирмы производить общественно эффективный объем выпуска? Существуют ли потери общества от такого налога? Если да, определите их и сравните с потерями общества из-за загрязнения. Каково распределение бремени данного налога между производителями и потребителями товара X? г) Можно ли побудить фирмы к производству общественно эффективного объема выпуска с помощью субсидии? Какова должна быть её природа и величина? Во сколько обошлась бы такая схема бюджету? Определите потери от такой субсидии и сравните их с потерями общества из-за загрязнения. Какая из двух корректирующих схем – налог или субсидия – предпочтительнее и почему? д) Приведите графическую иллюстрацию ко всем пунктам решения. (ЧФ, 5 с. 358). Предприятия двух конкурентных, максимизирующих прибыль фирм, расположены вдоль реки. Технология фирмы Y описывается производственной функцией вида 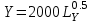 , где , где 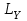 - число рабочих, нанимаемых в течении дня, а Y – выпуск печатной продукции в метрах. Фирма X, расположенная ниже по течению, имеет аналогичную производственную функцию, но на её выпуск может оказывать влияние выброс в реку химикалиев фирмой Y. Поэтому её производственная функция описывается уравнениями вида: - число рабочих, нанимаемых в течении дня, а Y – выпуск печатной продукции в метрах. Фирма X, расположенная ниже по течению, имеет аналогичную производственную функцию, но на её выпуск может оказывать влияние выброс в реку химикалиев фирмой Y. Поэтому её производственная функция описывается уравнениями вида: 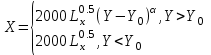 , где , где 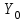 - выпуск, при котором загрязнение соответствует естественному уровню, создаваемому самой рекой. Если α=0, производство фирмы Y не оказывает воздействия на впуск фирмы X. Если же α<0, превышение Y над - выпуск, при котором загрязнение соответствует естественному уровню, создаваемому самой рекой. Если α=0, производство фирмы Y не оказывает воздействия на впуск фирмы X. Если же α<0, превышение Y над 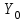 , вызывает сокращение выпуска фирмы X. Цена метра печатной продукции равна 1, и заработок одного рабочего составляет 50 в день. Определите для каждой из фирм число рабочих, нанимаемых в течение дня и дневной объем выпуска: , вызывает сокращение выпуска фирмы X. Цена метра печатной продукции равна 1, и заработок одного рабочего составляет 50 в день. Определите для каждой из фирм число рабочих, нанимаемых в течение дня и дневной объем выпуска:а) В отсутствие отрицательного внешнего эффекта. б) При его наличии, если α=-0,1 и 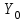 =38000. =38000.в) Как изменился бы совокупный выпуск двух предприятий по сравнению с выпуском в п. б), если бы фирмы объединились путем слияния, и менеджер образовавшейся фирмы перевел одного рабочего с предприятия Y на предприятие X при неизменности общего числа рабочих? г) Будет ли равновесный исход при слиянии двух фирм эффективным по Парето? (ЛП, 5, с. 283). Рассмотрите экономику с двумя благами – x и y и двумя потребителями – А и В. Предпочтения потребителей представимы функциями полезности вида 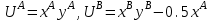 . Пусть каждый потребитель имеет по одной единице каждого блага. . Пусть каждый потребитель имеет по одной единице каждого блага.а) Охарактеризуйте внешнее воздействие, имеющее место в данной экономике. Придумайте содержательную экономическую ситуацию, которая моделируется в рассматриваемом примере. б) Найдите равновесие. в) Покажите, что равновесное распределение не будет Парето-оптимальным, указав Парето-улучшение. Обсудите, как должны быть перераспределены блага, чтобы достичь желаемого результата. г) Пусть полезность потребителя А задается следующим образом 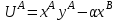 . Существует ли такое . Существует ли такое 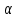 , что равновесное распределение будет Парето-оптимальным. , что равновесное распределение будет Парето-оптимальным.(НИУ – ВШЭ 2010 – 2011). Фирма 1 производит (а) Охарактеризуйте экстерналию, которая имеет место в этой задаче. (б) Какой выпуск будет у каждой фирмы, если фирмы не будут работать согласованно? (в) Найдите Парето эффективный выпуск каждой фирмы и сравните его с выпуском, полученным в пункте (б). (г) Предложите налоговую политику, которая могла бы привести к достижению Парето эффективного количества выпуска. (НИУ – ВШЭ 2010 – 2011). Пусть нефтяная отрасль в стране (а) Найдите равновесную добычу отрасли и каждой скважины. Имеет ли место различие между частными и общественными издержками в данной отрасли? (б) Предположим, что государство национализировало это месторождение. Сколько нефтяных скважин будет использовано в этом случае? Чему будет равна добыча нефти в целом и для каждой скважины в отдельности? (в) В качестве альтернативы национализации рассматривается выдача годовых лицензий на каждую скважину. Какова должна быть цена одной лицензии, чтобы на месторождении действовало оптимальное количество нефтяных скважин? (НИУ – ВШЭ 2010 – 2011). В экономике с двумя потребителями и одним предприятием предпочтения потребителей описываются следующими функциями полезности: (а) Охарактеризуйте внешнее воздействие, имеющее место в данной экономике. Придумайте экономическую ситуацию, которая моделируется в этой задаче. (б) Найдите равновесное распределение в данной экономике. (в) Является ли распределение, полученной в пункте (б) Парето оптимальным? Если нет, то найдите Парето оптимальное распределение. (г) Предложите какое-либо решение проблемы экстерналии в данной экономике. (НИУ – ВШЭ 2011 – 2012). Пасека находится по соседству с фруктовым садом. Пасечник должен решить, сколько ульев следует разместить в этом году. Аналогично, владелец сада определяет количество деревьев. Количество ульев будет обозначаться 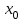 , а количество деревьев , а количество деревьев 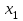 . Как известно, пчелы собирают мед с цветков, одновременно опыляя их. В результате чего производство меда, обозначаемое переменной . Как известно, пчелы собирают мед с цветков, одновременно опыляя их. В результате чего производство меда, обозначаемое переменной 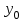 , также как и урожай фруктов, обозначаемый , также как и урожай фруктов, обозначаемый 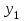 , зависят как от , зависят как от 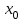 , так и от , так и от 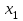 . Производственная функция пасеки такова . Производственная функция пасеки такова 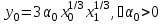 . Соответственно, производственная функция сада . Соответственно, производственная функция сада 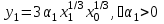 . .Издержки по устройству ульев заданы формулой 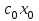 , а по посадке деревьев , а по посадке деревьев 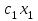 . Мед и фрукты продаются на рынке по ценам равным единице. Считаем, что рынок-это рынок совершенной конкуренции. . Мед и фрукты продаются на рынке по ценам равным единице. Считаем, что рынок-это рынок совершенной конкуренции.(а) Найдите прибыли производителя меда (пасечника) и производителя фруктов (садовода) как функции 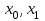 . Для заданного значения . Для заданного значения 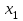 , каким будет оптимальный выбор пасечника? Другими словами, найдите зависимость , каким будет оптимальный выбор пасечника? Другими словами, найдите зависимость 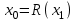 . Для заданного значения . Для заданного значения 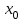 , каким будет оптимальный выбор садовода? Найдите зависимость , каким будет оптимальный выбор садовода? Найдите зависимость 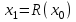 . Переменные . Переменные 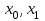 принимают действительные значения. принимают действительные значения.(б) В состоянии равновесия (при отсутствии каких-либо договоренностей между производителями) оптимальный выбор удовлетворяет системе уравнений  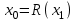 , , 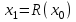 . Найдите равновесные значения . Найдите равновесные значения 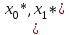 , а также соответствующие выпуски продукции , а также соответствующие выпуски продукции 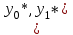 и равновесные значения прибылей обоих производителей и равновесные значения прибылей обоих производителей 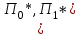 . .(в) На плоскости переменных 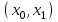 изобразите кривую, являющуюся графиком уравнения изобразите кривую, являющуюся графиком уравнения 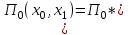 , обозначив ее , обозначив ее 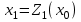 . Изобразите также кривую . Изобразите также кривую 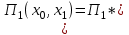 , обозначив ее , обозначив ее 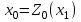 . Покажите, что найдется такой уровень . Покажите, что найдется такой уровень 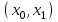 , при котором каждый из производителей получит прибыль, превышающую ту, которая была получена в состоянии равновесия. , при котором каждый из производителей получит прибыль, превышающую ту, которая была получена в состоянии равновесия.(г) Найдите оптимальный выбор 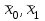 , при котором максимизируется суммарная прибыль производителей. Покажите, что полученная в результате максимизации сумма прибылей превосходит , при котором максимизируется суммарная прибыль производителей. Покажите, что полученная в результате максимизации сумма прибылей превосходит 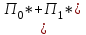 . Какие выводы можно сделать из решения данной задачи? . Какие выводы можно сделать из решения данной задачи?(ЧФ, 1, с. 367). Общественное благо G востребовано двумя группами потребителей. Готовность первой группы платить за это благо описывается функцией вида: 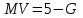 , а готовность второй – функцией вида: , а готовность второй – функцией вида: 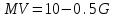 , предельные издержки производства блага G заданы функцией , предельные издержки производства блага G заданы функцией 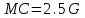 . .а) Каковы общественно эффективный объем предоставления блага G и готовность каждой из групп платить за него? б) Подсчитайте чистые потери общества при предоставлении 3 единиц блага, 5 единиц блага. в) Предположим, что вследствие технического прогресса предельные издержки производства блага G стали задаваться функцией 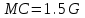 . Ответьте на вопросы а) и б) при этом условии. . Ответьте на вопросы а) и б) при этом условии.г) Приведите графическую иллюстрацию ко всем пунктам решения. (ЧФ, 3, с. 368). Пусть предпочтения потребителей в экономике задаются функциями вида 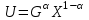 , где Х – частное благо, G – общественное благо, потребители имеют различные начальные запасы частного блага. Предельная норма трансформации частного блага в общественное равна единице. , где Х – частное благо, G – общественное благо, потребители имеют различные начальные запасы частного блага. Предельная норма трансформации частного блага в общественное равна единице. а) Насколько велика должна быть разница в величинах богатства потребителей, чтобы вклад потребителя 2 в поставки общественного блага был нулевым. б) Найдите цены Линдаля в данной экономике. (ЛП, 2, с. 288). В экономике с общественным благом имеется два потребителя с функциями полезности вида: 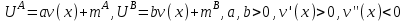 . Единственная фирма, принадлежащая потребителю А, имеет производственную функцию . Единственная фирма, принадлежащая потребителю А, имеет производственную функцию 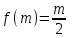 . Потребители владеют начальным запасом только частного блага. При . Потребители владеют начальным запасом только частного блага. При 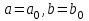 во внутреннем Парето-оптимальном распределении уровень общественного блага равен во внутреннем Парето-оптимальном распределении уровень общественного блага равен 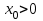 . А при . А при 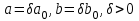 , в Парето-оптимальном распределении уровень общественного блага равен , в Парето-оптимальном распределении уровень общественного блага равен 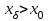 . Можно ли утверждать, что . Можно ли утверждать, что 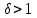 или или 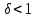 . Обоснуйте свой ответ. . Обоснуйте свой ответ.(ЛП, 5, с. 298). Рассмотрите экономику, в которой 3 потребителя имеют функции полезности вида: 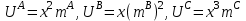 , где x- количество общественного блага, , где x- количество общественного блага, 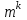 - потребление частного блага потребителем k. В экономике есть одна фирма, производящая общественное благо из частного, производственная функция которой может быть записана как - потребление частного блага потребителем k. В экономике есть одна фирма, производящая общественное благо из частного, производственная функция которой может быть записана как 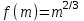 . Начального запаса общественного блага нет. Начальные запасы частного блага . Начального запаса общественного блага нет. Начальные запасы частного блага 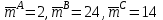 . Доли участия в прибыли фирмы: . Доли участия в прибыли фирмы: 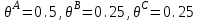 . .а) Найдите равновесие при добровольном финансировании общественного блага. б) Будет ли равновесное распределение Парето-оптимальным? (ЛП, 11, с. 323). Рассмотрите экономику с двумя благами – частным и общественным и двумя потребителями, которые обладают разными запасами частного блага, 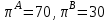 , но одинаковыми функциями полезности , но одинаковыми функциями полезности 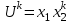 . Потребители в равных долях владеют фирмой, производящей из единицы частного блага единицу общественного. . Потребители в равных долях владеют фирмой, производящей из единицы частного блага единицу общественного.а) Найдите равновесие по Линдалю. б) Найдите множество внутренних Парето-оптимальных распределений. в) Реализуйте в равновесии по Линдалю произвольное внутренне Парето-оптимальное распределение. (ЛП, 12, с. 328). Рассмотрите экономику с двумя благами – общественным (x) и частным (m) и тремя потребителями, функции полезности которых возрастают по обоим благам. Потребители владеют фирмой, технология которой позволяет произвести x единиц общественного блага, используя 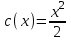 единиц частного. Потребители владеют начальными запасами частного блага единиц частного. Потребители владеют начальными запасами частного блага 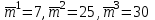 . Начальных запасов общественного блага в экономике нет. Известно, что во внутреннем равновесии Линдаля цены благ m и х соответственно . Начальных запасов общественного блага в экономике нет. Известно, что во внутреннем равновесии Линдаля цены благ m и х соответственно 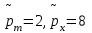 . Цены Линдаля для потребителей 1 и 2 соответственно . Цены Линдаля для потребителей 1 и 2 соответственно 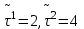 . Определите недостающие параметры равновесия Линдаля, которые возможно, используя имеющуюся информацию. . Определите недостающие параметры равновесия Линдаля, которые возможно, используя имеющуюся информацию.(ЛП, 16, с. 327). Рассмотрите экономику, где все потребители имеют квазилинейные функции полезности вида: 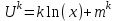 , где x- количество общественного блага, , где x- количество общественного блага, 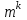 - потребление частного блага потребителем k. Всего в экономике 5 участников. В экономике есть одна фирма, которая производит общественное благо из частного с издержками - потребление частного блага потребителем k. Всего в экономике 5 участников. В экономике есть одна фирма, которая производит общественное благо из частного с издержками 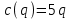 , где q – объем выпуска общественного блага.. Известно, что при , где q – объем выпуска общественного блага.. Известно, что при 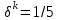 объем выпуска общественного блага в экономике с долевым финансированием при голосовании Парето-оптимален и составляет объем выпуска общественного блага в экономике с долевым финансированием при голосовании Парето-оптимален и составляет 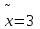 . Верно ли, что при следующем изменении долей финансирования . Верно ли, что при следующем изменении долей финансирования 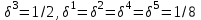 равновесный объем общественного блага пол прежнему будет Парето-оптимальным? равновесный объем общественного блага пол прежнему будет Парето-оптимальным? |
