лаб. Цель работы получить навыки моделирования объектов с сосредоточенными параметрами и построения графиков переходных процессов. Краткие теоретические сведения
 Скачать 124.05 Kb. Скачать 124.05 Kb.
|
|
Цель работы: получить навыки моделирования объектов с сосредоточенными параметрами и построения графиков переходных процессов. Краткие теоретические сведения Система – это декартово пересечение множеств (множество входных воздействий Х, и множество функций выхода У). Основным понятием в теории автоматического управления является понятие динамической системы описываемой дифференциальными уравнениями, наличие двух видов величин связанных между собой однонаправленной связью (за исключением систем с распределенными параметрами (СРП)). Наличие таких причин наследственных связей служат основой для изображения таких динамических систем с помощью структурных схем (рис 1.1). Рис. 1.1. Структурная схема динамической системы Динамическую систему, в которой протекает процесс регулирования, называют системой автоматического управления. При этом входные воздействия могут быть подразделены на два типа: управляющее воздействие 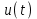 , возмущающее воздействие , возмущающее воздействие 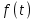 . . В  теории автоматического управления часто используют операторную форму записи дифференциальных уравнений, при этом формально записывают: теории автоматического управления часто используют операторную форму записи дифференциальных уравнений, при этом формально записывают: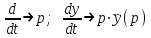 . .Положим, что имеется объект, на вход которого подается воздействие х(t), и функция выхода которого у(t). Передаточной функцией объекта называется отношение изображений по Лапласу при нулевых начальных условиях функции выхода к входному воздействию: 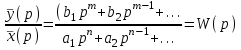 Числитель этой функции отражает реакцию системы на входное воздействие, а знаменатель характеризует собственное движение системы. Передаточной функцией многих объектов могут быть представлены в виде комбинаций передаточных функций элементарных стационарных звеньев. 1. Усилительное звено 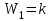 . .гдеk - заданное число (коэффициент усиления) 2. Апериодическое звено:  . .где T - заданный коэффициент (постоянная времени);p - оператор Лапласа; 3. Дифференцирующее звено 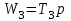 . .4. Интегрирующее звено: 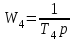 . .5. Изодромное звено: 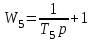 . .6. Форсирующее звено:  . .7. Колебательное звено: 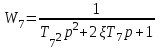 . .8. Звено с чистым запаздыванием: 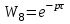 . .Заданиена лабораторную работу: Пусть имеется объект (система), блок-схема которого представлена на рисунке: Рис. 1.2. Блок-схема объекта. Принимая 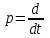 , и применяя метод конечных разностей , и применяя метод конечных разностей 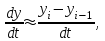 необходимо определить функцию выхода апериодического, дифференцирующего, интегрирующего, изодромного и форсирующегоэлементарных стационарных звеньев y(t) (y – значение функций выхода, t – время), если известно входное воздействие на систему необходимо определить функцию выхода апериодического, дифференцирующего, интегрирующего, изодромного и форсирующегоэлементарных стационарных звеньев y(t) (y – значение функций выхода, t – время), если известно входное воздействие на систему 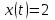 . Значения параметров Ti(равно 14) принять равными номеру студента в списке группы. Построить график переходного процесса разомкнутой системы. . Значения параметров Ti(равно 14) принять равными номеру студента в списке группы. Построить график переходного процесса разомкнутой системы.Ход работы: Апериодическое звено:  . .Вывод формулы: 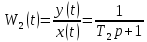 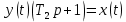 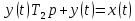 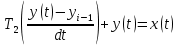 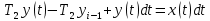 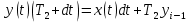 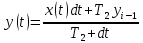 Подставляем значения:  Строим график полученной функции:  Дифференцирующее звено  dt y(t) Интегрирующее звено: 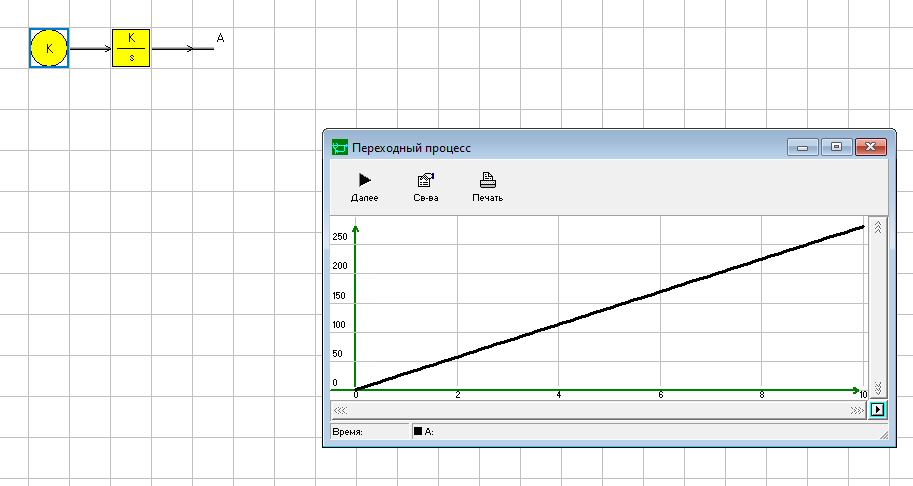 dt y(t) Изодромное звено: 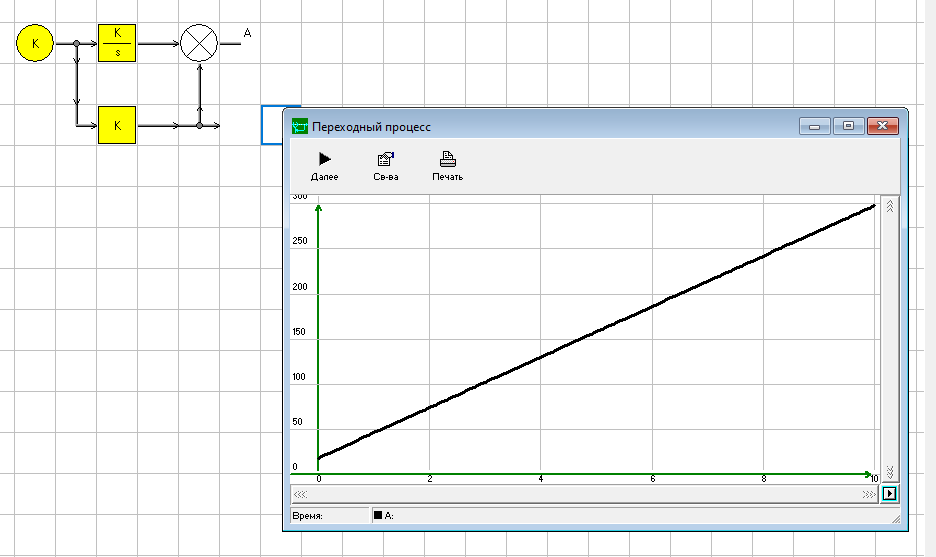 y(t) dt Форсирующее звено: 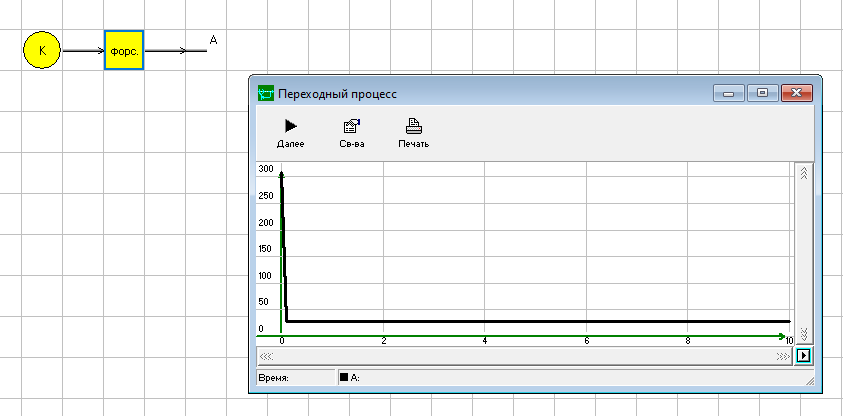 dt y(t) Вывод: данная лабораторная работа дала навыки моделирования объектов с сосредоточенными параметрами и построения графиков переходных процессов. |
