радиофизика билеты 1-4. Если удается выделить малый параметр, то уравнение удается преобразовать к виду
 Скачать 1.81 Mb. Скачать 1.81 Mb.
|
|
БИЛЕТ 1. 1. МММА применяется для анализа нелинейных уравнений, достаточно близких к линейным. Достаточно близкими к линейным, обычно называются колебания, для которых соответствующие дифференциальные уравнения хотя и являются нелинейными, но содержат некоторый параметр ε, входящий в эти уравнения так, что при нулевом значении ε они вырождаются в линейные дифференциальные уравнения с постоянными коэффициентами. При этом предполагается, что параметр ε является «малым». В общем виде, такие системы описываются дифференциальными уравнениями следующего вида: Если удается выделить малый параметр, то уравнение удается преобразовать к виду: В теории колебаний используется ряд методов основанных на малом параметре при нелинейной части дифференциальных уравнений 2го и более высоких порядков. Это метод возмещений Пуанкаре, метод медленно меняющихся амплитуд Ван-дер-Поля, метод амплитудной плоскости (метод Андронова-Витта), метод Боголюбова-Крылова, асимптотический метод Боголюбова-Митропольского и другие. Рассмотрим один из них – МММА. Данный метод так же, как и МГЛ, применим в тех случаях, когда возникающее колебание близко по форме к гармоническому, что обычно имеет место при использовании в автогенераторах, контура с достаточно высокой избирательностью. Уравнение, описывающее процессы в таких системах, может быть записано в виде: или в безразмерных переменных оно имеет вид: переходя от анализа одного дифференциального уравнения относительно одной переменной, к анализу системы двух уравнений относительно двух переменных: 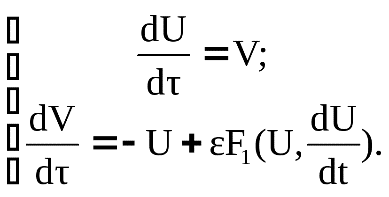 (2) (2)Если параметр ε равен 0, то решение уравнения (2) имеет вид: 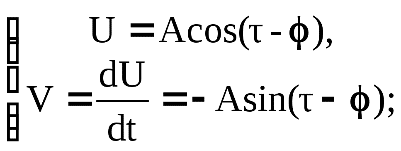 (3) (3)где А и φ – произвольные постоянные. В методе медленно меняющихся амплитуд решение системы уравнений (1) ищем в виде выражений, отличающихся от (3) тем, что амплитуда А и фаза φ считаются некоторыми функциями времени А(τ) и φ(τ). Тогда 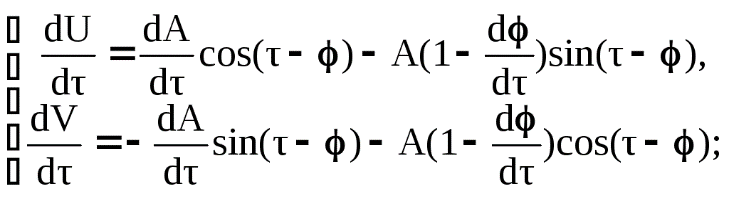 (4) (4)Подставляя (3) и (4) в (2), получаем: 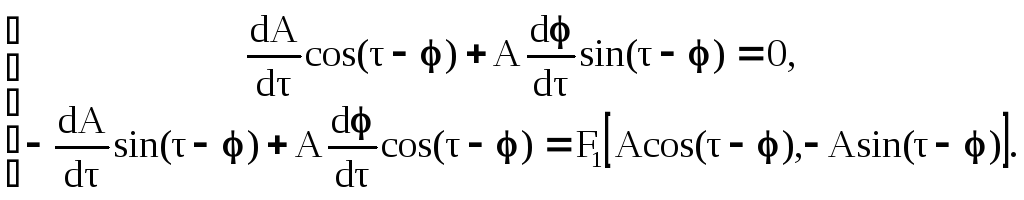 Решение этих уравнений относительно 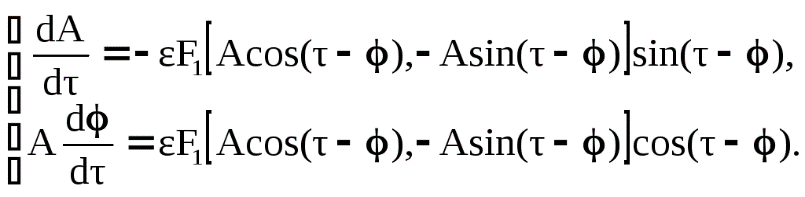 (5) (5)Правые части этих уравнений являются функциями времени (α = τ – φ ), с периодом 2π, что позволяет разложить их в ряд Фурье: 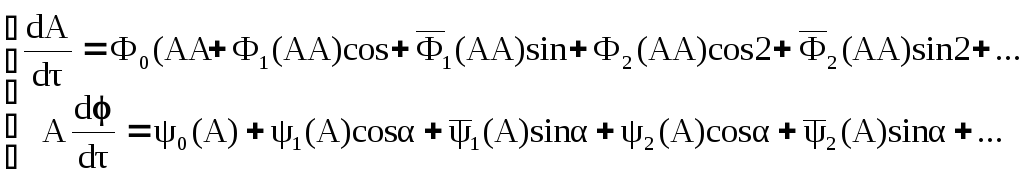 (6) (6)Коэффициенты рядов Фурье оказываются функциями амплитуд А. Поскольку до сих пор никаких ограничений на зависимость А(τ) и φ(τ) не накладывалось, уравнения (5) являются столь же точными, как и (2) или (1). Теперь примем во внимание, что при наличии малого параметра амплитуда А и фаза φ могут изменяться только медленно, т.е. на малую величину за период 2π. Поэтому при этом можно принять, что в пределах одного периода изменения А и φ происходят с постоянными средними скоростями, соответствующими первым слагаемым рядов Фурье, стоящими в правых частях уравнений (6). Результаты такого усреднения правых частей уравнений (6) получаем в виде: 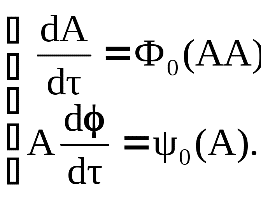 (7) (7)где: 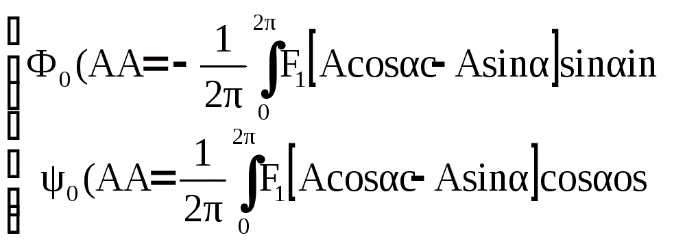 (8) (8)Уравнения (7) называются укороченными, т.к. они получаются в результате отбрасывания ряда слагаемых уравнения (6) или уравнениями медленно меняющихся амплитуд и фаз, поскольку они справедливы в тех случаях, когда А и φ медленно (мало) меняются за период колебаний. Из (7) следует, что в процессе установления колебаний, т.е. при изменении амплитуды А, происходит изменение и величины ω/ = также меняется. 2. Вспомним классическое определение корреляционной функции, известное из курса статистики. Пусть в некотором эксперименте получены два множества результатов измерений: , где – например, нагрузка, приложенная к конструкции; – общее количество измерений. Измерения, проведенные при различных значениях нагрузки, приведут к зависимостям типа показанных на рисунке 1.12. В идеальном случае измерения дают точную линейную зависимость между и (рисунок 1.12, а). Неправильная постановка эксперимента может привести к другой крайности, когда между нагрузкой и напряжением отсутствует какая-либо связь (рисунок 1.12, б). Возможны зависимости и промежуточного вида. На рисунке 1.12, в угадывается линейная связь между и , но точного аналитического выражения для нее записать нельзя из-за случайного характера этой связи или ошибок измерений. На рисунке 1.12, г между и существует точная аналитическая зависимость, но она нелинейна. 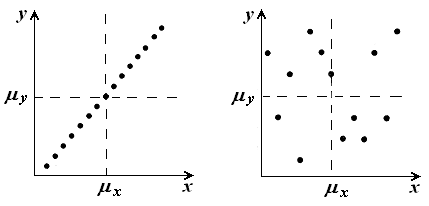 а) линейная корреляция; б) отсутствие корреляции 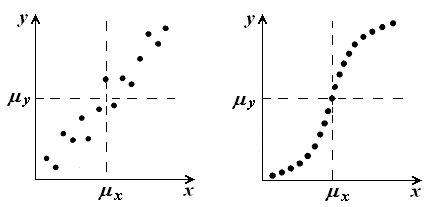 в) умеренная линейная корреляция; г) нелинейная корреляция Рисунок 1.12 – Различные степени корреляции Меру линейности связи и можно задать как усредненное произведение разностей 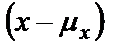 и и 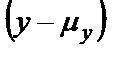 . Если размер выборки стремится к бесконечности, то предел этого усредненного произведения определяет корреляцию между и : . Если размер выборки стремится к бесконечности, то предел этого усредненного произведения определяет корреляцию между и :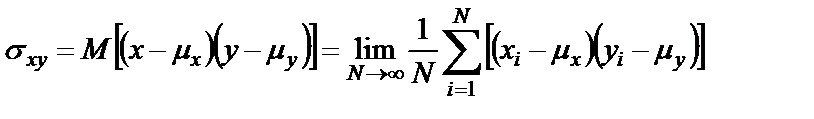 . (1.24) . (1.24)Наибольшее возможное значение корреляции двух случайных величин определяется равенством 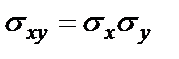 , ,поэтому в качестве меры коррелированности обычно используют отношение 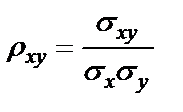 , , Величину 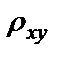 называют коэффициентом корреляции, который характеризует меру линейной зависимости между двумя переменными и . называют коэффициентом корреляции, который характеризует меру линейной зависимости между двумя переменными и .Пусть теперь интересующие нас данные являются результатами измерения двух случайных процессов 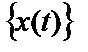 , , 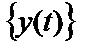 , которые предполагаются стационарными и эргодическими, так, что их можно описать индивидуальными реализациями. Понятие корреляции случайных процессов вводят, используя дополнительную переменную – временной сдвиг между процессами, или запаздывание , которые предполагаются стационарными и эргодическими, так, что их можно описать индивидуальными реализациями. Понятие корреляции случайных процессов вводят, используя дополнительную переменную – временной сдвиг между процессами, или запаздывание 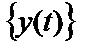 относительно относительно 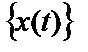 . .Взаимная корреляционная функция двух случайных процессов для произвольного сдвига вводится по соотношению Для стационарных СП справедливо выражение 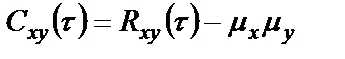 , (1.27) , (1.27)где 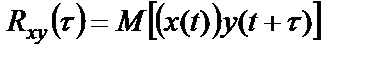 – взаимная ковариационная функция двух процессов. – взаимная ковариационная функция двух процессов.Случайные процессы считаются некоррелированными, если их взаимная корреляционная функция равна нулю. Согласно (1.27) взаимные корреляционная и ковариационная функции двух случайных процессов совпадают, если средние значения обоих процессов равны нулю. В частном случае, когда случайные процессы совпадают 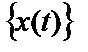 = == 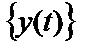 , связь между корреляционной и ковариационной функциями принимает вид , связь между корреляционной и ковариационной функциями принимает вид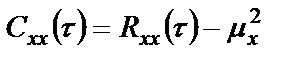 , (1.28) , (1.28)где 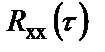 – ковариационная функция процесса – ковариационная функция процесса 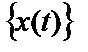 , определяемая как , определяемая как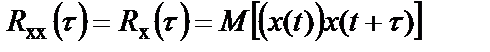 . (1.29) . (1.29)Свойства ковариационной и корреляционной функций стационарного СП, согласно выражениям (1.19), (1.28), (1.29), определяются следующими соотношениями: 1. 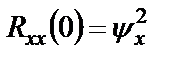 , , 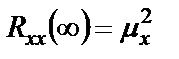 , , 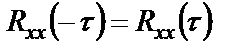 ; ;2. 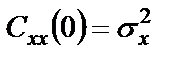 , , 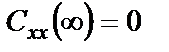 , , 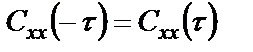 . .Рисунок 1.13 иллюстрирует свойства ковариационной функции. 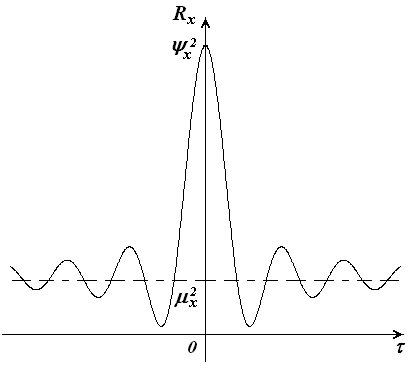 Рисунок 1.13 – Типичная ковариационная функция С увеличением временного сдвига функция корреляции случайного процесса стремится к нулю: 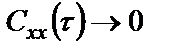 при при Чем быстрее убывает эта функция, тем меньше оказывается статистическая связь между мгновенными значениями случайного процесса в два различных момента времени. Числовой характеристикой, служащей для оценки скорости изменения реализаций случайного процесса, является интервал корреляции: 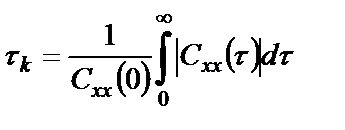 . (1.30) . (1.30)Если известна информация о поведении какой-либо реализации случайного процесса в прошлом, то возможен вероятностный прогноз его значений на время порядка По аналогии с коэффициентом корреляции для двух случайных величин вводят понятие нормированной корреляционной функции, определяющей степень линейной зависимости двух случайных процессов 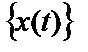 и и 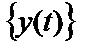 при временном сдвиге процесса при временном сдвиге процесса 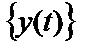 относительно относительно 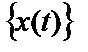 на величину : на величину :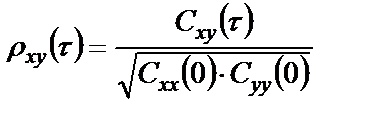 , (1.31) , (1.31)причем 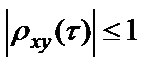 для всех . для всех .Взаимная ковариационная функция двух процессов применяется во многих важных практических случаях. 3. Рассмотрим оптическую схему опыта Юнга (рис. 25). Если источник света не точечный и имеет размер 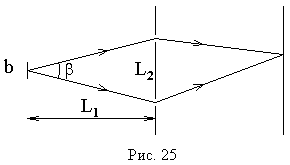 Будем считать, что источник света представляет собой полоску постоянной ширины и яркости. Картина полностью "смажется", если интерференционные картины от крайних точек источника будут сдвинуты относительно друг друга ровно на одну полосу интерференции, что соответствует изменению разности хода на одну длину волны Как видно из рис. 25 при переходе от одной точки источника света к другой точке разность хода может измениться только слева от экрана с двумя щелями. Выясним, какому перемещению Представьте себе, что свет на рис. 25 идет справа налево. Тогда слева получим полосы интерференции от двух щелей. Переход от одной полосы к другой соответствует изменению разности хода на при котором интерференционные полосы полностью "смажутся". БИЛЕТ 2. 1.   2. Нормальный (гауссовский) закон распределения случайных величин чаще других встречается в природе. Нормальный процесс особенно характерен для помех в каналах связи. Он очень удобен для анализа. Поэтому случайные процессы, распределение которых не слишком отличается от нормального часто заменяют гауссовским процессом. Одномерная плотность вероятности нормального процесса определяется выражением: 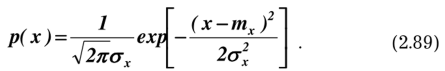 В данном случае будет рассматриваться стационарный и эргодический гауссовский процесс. Графики плотности вероятности при нормальном законе для некоторых значений 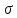 х изображены на рис. 2.24. Функция р(х) симметрична относительно среднего значения. Чем больше х изображены на рис. 2.24. Функция р(х) симметрична относительно среднего значения. Чем больше 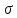 х, меньше максимум, а кривая становится более пологой. х, меньше максимум, а кривая становится более пологой.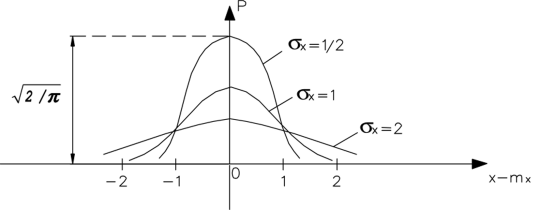 Рис. 2.24. Одномерная плотность вероятности нормального распределения Широкое распространение нормального закона распределения в природе объясняется тем, что при суммировании достаточно большого числа независимых или слабо зависимых случайных величин распределение суммы близко к нормальному при любом распределении отдельных слагаемых. Это положение, сформулированное в 1901 г. А. М. Ляпуновым, получило название центральной предельной теоремы. 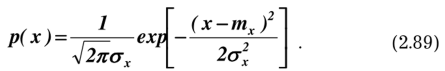 Наглядными физическими примерами случайного процесса с нормальным законом распределения являются шумы, обусловленные тепловым движением свободных электронов в проводниках электрической цепи или дробовым эффектом в электронных приборах. Не только шумы и помехи, но и полезные сигналы, являющиеся суммой большого числа независимых случайных элементарных сигналов, например, гармонических колебаний со случайной фазой или амплитудой, часто можно трактовать как гауссовские случайные процессы. На основе функции р(х) можно найти относительное время пребьюания сигнала x(t) в определенном интервале уровней, отношение максимальных значений к среднеквадратическому (пик фактора) и ряд других важных для практики параметров случайного сигнала. Отношение времени пребывания x(t) в заданном интервале к общему времени наблюдения можно трактовать как вероятность попадания x(t) в указанный интервал. При этом следует заметить, что данные о распределении вероятностей не дают никаких представлений о поведении функции x(t) во времени. 3. Любой ОКГ независимо от конструктивного выполнения содержит следующие основные элементы: 1) рабочее тело, состоящее из ансамбля атомов или молекул, для которых может быть создана инверсия заселенностей; 2) систему, позволяющую осуществлять инверсию; 3) оптический резонатор; 4) устройство для вывода энергии из резонатора; 5) систему управления концентрацией энергии и пространственным положением полученного пучка света; 6) различные специальные системы, связанные с конкретным применением ОКГ. В ОКГ применяют следующие виды накачки: а) оптическую - за счет облучения вещества мощным световым потоком; б) электрическую, осуществляемую при прохождении через вещество электрического тока; в) химическую, когда инверсия возникает за счет химической реакции, в которой принимает участие рабочее вещество, и т.д. В зависимости от режима работы ОКГ различают устройства, работающие в непрерывном и импульсно-периодическом режимах. Существующие лазеры по роду материалов, используемых для получения индуцированного излучения, подразделяют на четыре основных типа: твердотельные с оптическим возбуждением, полупроводниковые (инжекционные), жидкостные и газовые. 1. Лазеры твердотельные с оптической накачкой. В лазерах этого типа излучателем - активным элементом - является твердое тело. В таких ОКГ основная масса диэлектрика (матрица) непосредственного участия в процессе генерации индуцированного излучения не принимает. Стимулированное излучение и генерация связаны с происходящими в матрице переходами атомов активатора, содержащегося в ней в количестве 0,01 -10%. Материалом матрицы служат кристаллы щелочно-земельных фторидов, вольфраматов или молибдатов, синтетического рубина, стекла различных составов. Активирующими примесями являются различные редкоземельные элементы, а также хром и уран. Длительность импульса твердотельных ОКГ определяется индуктивностью, включаемой в цепь конденсаторной батареи, и обычно колеблется в пределах 0,1 -10 мс. Частота повторения импульсов зависит в основном от условий охлаждения и характеристик импульсной лампы. КПД твердотельных лазеров относительно невысок, поскольку значительная часть подводимой к лампе накачки энергии превращается в теплоту. Лазерное излучение на поверхности обрабатываемой детали фокусируется с помощью сферической или цилиндрической оптики. В первом случае луч фокусируется в точку, во втором - в линию. 2. Твердотельные полупроводниковые лазеры. Лазеры этого типа отличаются от рубиновых тем, что в качестве излучающего свет вещества в них используется кусочек полупроводника. Полупроводниковые лазеры, в которых возбуждение осуществляется при инжекции носителей заряда через p-n-переход, называют инжекционными. Полупроводниковые инжекционные лазеры характеризуются очень высоким преобразованием электрической энергии в когерентное излучение (до 100%) и могут работать в непрерывном режиме. 3. Жидкостные лазеры. Их основное преимущество - возможность циркуляции жидкости с целью ее охлаждения, что позволяет получать большие энергии и мощности излучения в импульсном и непрерывном режимах. Созданы лазеры на основе растворов редкоземельных ионов в ряде неорганических жидкостей, а также лазеры непрерывного и импульсного действия, у которых в качестве активной среды используются растворы органических красителей. В резонатор жидкостных лазеров вместо стеклянного стержня помещают кювету с раствором. Инверсия осуществляется за счет накачки от импульсных ламп. Коэффициент преобразования энергии оптической накачки в энергию генерации достигает 50%. Лазеры, работающие на неорганических активных жидкостях, обладают большими импульсными энергиями при значительной средней мощности, при этом они генерируют излучение с узким спектром частот. 4.Газовые лазеры.Стеклянная трубка наполняется специальной газовой смесью. В ее торцы впаивают два электрода и к ним подводят напряжение от ИП. В трубке возбуждается газовый разряд. Для газовых лазеров подбирают специальные активные смеси, атомы или молекулы которых могут некоторое время находиться в метастабильном состоянии. По сравнению с твердыми телами и жидкостями газы обладают меньшей плотностью и более высокой однородностью, что не вызывает искажения светового луча, его рассеяния и потерь энергии. В результате направленность лазерного излучения в газах резко увеличивается, достигая предела, обусловленного дифракцией. В качестве активных газов в ОКГ применяют аргон, неон, криптон, ксенон, смеси гелия и неона, углекислый газ с добавкой азота и гелия. Газовые ОКГ подразделяют на три большие группы: лазеры на атомных, ионных и молекулярных переходах. БИЛЕТ 3. 1. Рассмотрим задачу об отражении и прохождении плоской электромагнитной волны с длиной волны от плоской границы раздела между двумя средами (рис. 3.3) , одно из которых при заполнено диэлектриком без потерь со значением относительной диэлектрической и магнитной проницаемости соответственно равными и , а другое при - вакуум ( ).
|