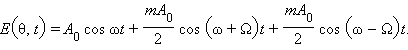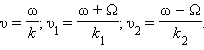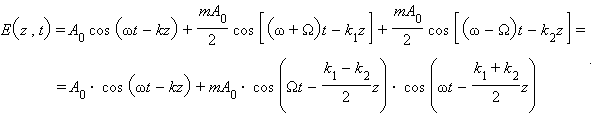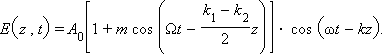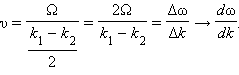радиофизика билеты 1-4. Если удается выделить малый параметр, то уравнение удается преобразовать к виду
 Скачать 1.81 Mb. Скачать 1.81 Mb.
|
|
Фазовой скоростью v монохроматичной волны принято называть скорость распространения волнового фронта. В среде с показателем преломления n фазовая скорость υ равна
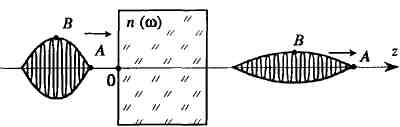
Здесь – круговая частота, k – волновое число, c – скорость света в вакууме. Как показывает опыт, все без исключения среды обладают дисперсионными свойствами – волны разных частот распространяются в средах с различными фазовыми скоростями. Это явление называют дисперсией. Закон дисперсии можно задать либо в виде зависимости показателя преломления от частоты , либо в виде функции , либо, наконец, в виде зависимости волнового числа от частоты . В качестве аргумента в законе дисперсии может быть вместо использована длина волны в среде. При распространении монохроматической волны в среде с дисперсией никаких особых явлений не наблюдается; волна распространяется со своей фазовой скоростью, которая определяется значением показателя преломления на частоте волны. Но если в диспергирующей среде одновременно распространяется группа волн разных частот, то по мере распространения волн возникают фазовые сдвиги между отдельными спектральными компонентами. При этом происходит деформация формы суммарного процесса. Если на входе в диспергирующую среду возмущение имело вид импульса (волнового пакета) определенной формы, то после прохождения некоторого слоя форма импульса может существенно измениться. В общем случае наблюдается расплывание волнового пакета. Рис 6.1. иллюстрирует это утверждение. По теореме Фурье волновой пакет 1 можно представить в виде суперпозиции монохроматических волн разных частот. На выходе все спектральные компоненты будут вновь складываться, образуя новый волновой пакет 2. Деформация волнового пакета происходит вследствие изменения фазовых соотношений.
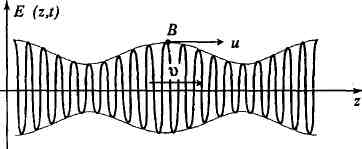
Вопрос о скорости распространения волнового пакета в среде с дисперсией достаточно сложен и неоднозначен. Можно, например, следить за перемещением переднего фронта (точка A на рис. 6.1). Обычно в теории рассматривается так называемая групповая скорость, то есть скорость перемещения центра волновой группы или точки с максимальным значением амплитуды (точка B). Рассмотрим простой случай – распространение амплитудно-модулированной волны. При z = 0, то есть на входе в диспергирующую среду, колебание можно записать в виде
Этот процесс может быть представлен в виде суперпозиции трех синусоидальных колебаний с частотами , , :
Каждая из этих спектральных компонент будет распространяться в среде со своей фазовой скоростью:
Таким образом при z > 0 можно записать:
Рассмотрим случай достаточно малых значений z, удовлетворяющих условию
В этом случае высокочастотные колебания частоты , описываемые 1-ым и 2-ым слагаемыми в (6.5), практически не отличаются по фазе и могут быть объединены. Тогда
Функцию E(z, t) можно рассматривать как амплитудно-модулированную волну с медленно изменяющейся во времени и пространстве амплитудой  . «Моментальная фотография» этой функции изображена на рис. 6.2. . «Моментальная фотография» этой функции изображена на рис. 6.2.
Как видно из (6.7) модулируемая волна распространяется с фазовой скоростью . Скорость распространения огибающей, то есть модулирующей волны, есть
Это и есть групповая скорость. Волновой пакет (цуг волн)— определённая совокупность волн, обладающих разными частотами, которые описывают обладающую волновыми свойствами формацию, в общем случае ограниченную во времени и пространстве. Так, в квантовой механике описание частицы в виде волновых пакетов способствовало принятию статистической интерпретации квадрата модуля волновой функции. Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является различие фазовых скоростей распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и, следовательно, цвета). Обычно, чем меньше длина световой волны, тем больше показатель преломления среды для неё и тем меньше фазовая скорость волны в среде: у света красного цвета фазовая скорость распространения в среде максимальна, а степень преломления — минимальна, у света фиолетового цвета фазовая скорость распространения в среде минимальна, а степень преломления — максимальна. Однако в некоторых веществах (например, в парах иода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают. Говоря строже, аномальная дисперсия широко распространена, например, она наблюдается практически у всех газов на частотах вблизи линий поглощения, однако у паров иода она достаточно удобна для наблюдения в оптическом диапазоне, где они очень сильно поглощают свет. Дисперсия света позволила впервые вполне убедительно показать составную природу белого света. Белый свет разлагается в спектр в результате прохождения через дифракционную решётку или отражения от неё (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному. По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только к электромагнитной волне, но к любому волновому процессу. Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая). Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем, в том числе фотографических и видеообъективов. |