радиофизика билеты 1-4. Если удается выделить малый параметр, то уравнение удается преобразовать к виду
 Скачать 1.81 Mb. Скачать 1.81 Mb.
|
|
Предположим, что электромагнитная волна падает на границу раздела перпендикулярно границе раздела, т.е. распространяется в положительном направлении оси (рис. 3.3). Для определённости будем считать, падающую волну с вектором напряженности электрического поля, направленным вдоль оси . Тогда вектор напряженности магнитного поля будет направлен вдоль оси . Отметим, что в силу симметрии рассматриваемой задачи результат её решения не должен вообще зависеть от выбранной поляризации электромагнитной волны. Действительно для любой электромагнитной волны, падающей нормально к поверхности раздела вакуум/диэлектрик всегда можно ориентировать оси декартовой системы координат, чтобы ось была направлена вдоль направления колебаний напряженности электрического поля падающей волны. Итак, в соответствии со сделанными предположениями можно написать следующие выражения для комплексных амплитуд напряженности электрического и магнитного полей :
где - амплитуда падающей волны1; - волновое число падающей волны; ом - волновое сопротивление вакуума. В результате взаимодействия падающей волны с границей раздела в левом полупространстве ( ) возникнет отраженная волна с амплитудой , распространяющаяся в отрицательном направлении оси . Кроме того, в правом полупространстве ( ) будет распространяться прошедшая волна с амплитудой . Очевидно, направление колебаний векторов напряженности электрического поля всех волн параллельно оси , а направление колебаний векторов напряженности магнитного поля параллельно оси , как в падающей волне. Рассмотрим выражение для комплексных амплитуд векторов напряженностей электрического и магнитного полей слева и справа от границы раздела вакуум/диэлектрик: а) для левого полупространства :
б) для правого полупространства :
где - волновое число электромагнитной волны в среде с показателем преломления ; - волновое сопротивление среды распространения с показателем преломления ( в частном случае среды с магнитной проницаемостью равной единице ( ) . Для решения задачи взаимодействия падающей электромагнитной волны с границей раздела двух сред надо определить неизвестные коэффициенты и . В дальнейшем удобно вместо этих коэффициентов рассматривать их значения и , отнормированные на амплитуду падающей волны, т. е.:
Определённые соотношением (3.31) коэффициенты и называются соответственно коэффициентами отражения и прохождения электромагнитной волны по амплитуде. Для определения неизвестных коэффициентов r и d используем условия непрерывности тангенциальных компонент векторов напряженности электрического и магнитного полей на границе раздела двух сред. В рассматриваемой задаче компоненты векторов напряженностей всех волн: падающей, отраженной и прошедшей являются тангенциальными, поскольку они параллельны плоской границе раздела вакуум - диэлектрик, соответствующей плоскости . Таким образом, неизвестные коэффициенты и могут быть найдены из уравнений, получающихся после приравнивания при соответственно и , а также и , каждое из которых определено в (3.29) и (3.30):
Отсюда находим, что искомые коэффициенты и , в случае произвольных и равны:
В частном случае для имеем и из выражений (3.33) следует, что:
Из выражения (3.34) следует, что при коэффициент отражения по амплитуде . Это означает, что при отражении электромагнитной волны от границы раздела вакуум/диэлектрик фаза отраженной волны отличается на 1800 от фазы падающей волны. Этот эффект имеет место также и в более общем случае, когда электромагнитная волна распространяется через границу раздела из среды с меньшей оптической плотностью в среду, где оптическая плотность больше, т.е. . В самом деле, если ввести в рассмотрение относительный показатель преломления двух сред с помощью выражения:
и повторить вывод формул (3.33) и (3.34), то получатся выражения, отличающиеся от полученных ранее тем , что в них вместо показателя преломления будет относительный показатель преломления , а (0 и ( являются волновыми сопротивлениями сред соответственно с оптической плотностью . Тогда отрицательные значения коэффициента отражения r будут иметь место при , что и является подтверждением справедливости сделанного выше обобщения. Рассчитаем теперь средние плотности потоков мощности , которые переносятся соответственно падающей, отражённой и прошедшей через границу раздела двух сред электромагнитными волнами. Для этой цели определим вектора Пойнтинга каждой из перечисленных волн с помощью формулы (1.54), использующей комплексные амплитуды векторов электрического и магнитного поля электромагнитной волны:
Найдем сумму плотностей потоков энергии, переносимых прошедшей и отражённой волны с учетом выражений (3.34) для коэффициентов r и d :
Из этого выражения следует, что при прохождении электромагнитной волны через границу раздела вакуум/диэлектрик выполняется закон сохранения плотностей потоков энергии, поскольку поток энергии падающей волны перераспределяется между потоками энергии отраженной и прошедшей через границу раздела волнами. В силу замечания, сделанного выше, закон сохранения плотностей потоков энергии (3.37) остаётся справедливым и при распространении волны из одной среды с показателем преломления в другую среду с показателем преломления . Наряду с коэффициентами отражения волны по амплитуде вводятся коэффициенты отражения и прохождения электромагнитной волны по мощности, определяемые в соответствии с выражениями (3.36) :
В cледствии закона сохранения потоков энергии (3.37) коэффициенты отражения и прохождения электромагнитной волны по мощности связаны между собой соотношением
позволяющим находить один из неизвестных коэффициентов отражения/прохождения по мощности, если известен другой. При падении плоских электромагнитных волн на границу раздела двух сред при определенных условиях коэффициент отражения может обращаться в нуль. Угол падения, при котором падающая волна полностью, без отражения, проникает из одной среды в другую, называется углом Брюстера и обозначается как φБ. φБ удовлетворяет одному из двух уравнений: при перпендикулярной поляризации либо при параллельной поляризации. Здесь под ψБ подразумевается угол преломления, соответствующий углу падения φБ. Легко видеть, что уравнения (4.35) и (4.36) взаимно противоречат друг другу, т. е. явление полного преломления можно наблюдать либо при перпендикулярной, либо при параллельной поляризации. Рассмотрим наиболее часто встречающийся случай, когда обе граничащие среды являются немагнитными (µ1=µ2=l), в то время как оптическая плотность второй среды больше, чем первой (ε2>ε1). Из данных предположений, во-первых, следует что Zс1>Zc2. Во-вторых, в силу закона Снелля φ>ψ, т. е. cos φ Обращаясь к формулам (4.35) и (4.36), видим, что первое из этих уравнений в рамках сделанных предположений принципиально не может иметь решений. Таким образом, угол Брюстера при падении плоской электромагнитной волны на немагнитный диэлектрик может существовать лишь при параллельной поляризации. Сравнение графиков, зависимостей коэффициентов отражения для волн обеих поляризаций, представленных на рис. 4.8, иллюстрирует понятие угла Брюстера.Явление полного преломления может иметь полезные технические приложения. Так, пластинка из диэлектрика, установленная под углом Брюстера по отношению к направлению распространения падающей волны, не создает отражений. В то же время эта пластинка, может играть роль важного конструктивного элемента, обеспечивая, например, вакуумное уплотнение какого-либо прибора. Полное внутреннее отражение — внутреннее отражение, при условии, что угол падения превосходит некоторый критический угол. При этом падающая волна отражается полностью, и значение коэффициента отраженияпревосходит его самые большие значения для полированных поверхностей. Коэффициент отражения при полном внутреннем отражении не зависит отдлины волны.В оптике этоявлениенаблюдается для широкого спектраэлектромагнитного излучения, включаярентгеновский диапазон.В геометрической оптике явление объясняется в рамкахзакона Снелла. Учитывая, что угол преломления не может превышать 90°, получаем, что при угле падения,синускоторого больше отношения меньшего показателя преломления к большему показателю, электромагнитная волна должна полностью отражаться в первую среду. В соответствии с волновой теорией явления, электромагнитная волна всё же проникает во вторую среду — там распространяется так называемая «неоднородная волна», которая экспоненциальнозатухает и энергию с собой не уносит. Характерная глубина проникновения неоднородной волны во вторую среду порядка длины волны. Нарушенное полное внутреннее отражение — явление нарушения полного внутреннего отражения из-за поглощения отражающей средой части излучения. Широко применяется в лабораторной практике и оптической промышленности. 2. В случае многомерной случайной величины (случайного вектора) характеристикой разброса ее составляющих и связей между ними является ковариационная матрица. Ковариационная матрица определяется как математическое ожидание произведения центрированного случайного вектора на тот же, но транспонированный вектор: где 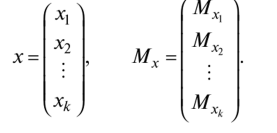 Ковариационная матрица имеет вид 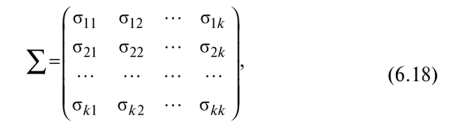 где по диагонали стоят дисперсии координат случайного вектора on=DXi, o22=DX2, окк = DXk, а остальные элементы представляют собой ковариации между координатами °12=M'xix2j а1* = M-jc,** > •••• Ковариационная матрица является симметрической матрицей, т.е. Для примера рассмотрим ковариационную матрицу двумерного вектора 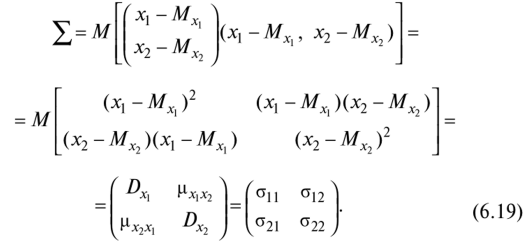 Аналогично получается ковариационная матрица для любого /^-мерного вектора. Дисперсии координат можно представить в виде где Gi,C2,...,0? — средние квадратичные отклонения координат случайного вектора. Коэффициентом корреляции называется, как известно, отношение ковариации к произведению средних квадратичных отклонений: 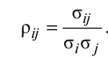 После нормирования по последнему соотношению членов ковариационной матрицы получают корреляционную матрицу 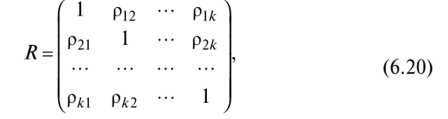 которая является симметрической и неотрицательно определенной. Многомерным аналогом дисперсии случайной величины является обобщенная дисперсия, под которой понимается величина определителя ковариационной матрицы Другой общей характеристикой степени разброса многомерной случайной величины является след ковариационной матрицы где <5[ 1, о22,..., Скк — диагональные элементы ковариационной матрицы. Часто в многомерном статистическом анализе используется нормальное распределение. Обобщением нормальной плотности вероятности на случай ^-мерного случайного вектора является функция 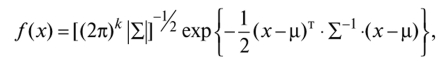 где ц = (pj, ц2, М^)т— вектор-столбец математических ожиданий; |Х| — определитель ковариационной матрицы X; ?-1 — обратная ковариационная матрица. Матрица X-1, обратная к матрице X размерности пх п, может быть получена различными способами. Одним из них является метод Жордана—Гаусса. В этом случае составляется матричное уравнение где х — вектор-столбец переменных, число которых равно я; b — я-мерный вектор-столбец правых частей. Умножим слева уравнение (6.21) на обратную матрицу ХГ1: Так как произведение обратной матрицы на данную дает единичную матрицу Е, то Если вместо b взять единичный вектор 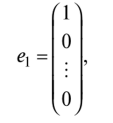 то произведение X-1 -ех дает первый столбец обратной матрицы. Если же взять второй единичный вектор 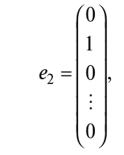 то произведение Е 1 е2 дает первый столбец обратной матрицы и т.д. Таким образом, последовательно решая уравнения методом Жордана—Гаусса, получаем все столбцы обратной матрицы. Другой метод получения матрицы, обратной к матрице Е, связан с вычислением алгебраических дополнений AtJ.= (/= 1, 2,..., п; j = 1, 2, ..., п) к элементам данной матрицы Е, подстановкой их вместо элементов матрицы Е и транспортированием такой матрицы: 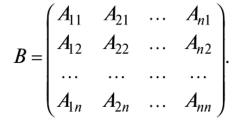 Обратная матрица получается после деления элементов В на определитель матрицы Е: Важной особенностью получения обратной матрицы в данном случае является то, что ковариационная матрица Е является слабо обусловленной. Это приводит к тому, что при обращении таких матриц могут возникать достаточно серьезные ошибки. Все это требует обеспечения необходимой точности вычислительного процесса или использования специальных методов при вычислении таких матриц. 3. К химическим лазерам относятся такие лазеры, в которых инверсная населенность достигается за счет энергии, выделяемой в результате прохождения экзотермической химической реакции. Эти реакции могут быть нескольких типов: A+B→AB– реакция синтеза, ABC→A+BC– реакция разложения, A+BC→AB+C– реакция замещения. В любом из рассмотренных вариантов энергия, которая выделяется в результате реакции, должна пойти на возбуждение колебательных или электронных состояний молекулы - продукта реакции. Если экзотермическая реакция происходит между веществами, находящимися в газовой фазе, то наиболее эффективным каналом высвобождаемой тепловой энергии является преобразование ее в энергию колебательно-вращательных состояний продукта реакции. Это объясняется прежде всего тем, что скорости колебательно-вращательной релаксации в молекулах существенно меньше по сравнению со скоростями электронной релаксации. Кроме того, в результате реакций в процессе образования новых молекул перестраиваются химические связи, и высвобождаемая энергия идет на перестраивание этих химических связей через колебательные состояния. Таким образом, в химических лазерах генерация осуществляется на переходах между колебательно-вращательными состояниями основного электронного состояния, а активная среда находится в газовой фазе. Для того, чтобы между какой-либо парой уровней возникла инверсная населенность, необходимо, чтобы скорости колебательной релаксации между этими уровнями существенно отличались: скорость релаксации верхнего лазерного уровня должна быть меньше, чем нижнего. В качестве молекул активной среды необходимо использовать наиболее простые (желательно, двухатомные) молекулы, обладающие минимальным количеством колебательных степеней свободы. В противном случае высвобождаемая в химической реакции энергия будет идти на возбуждение множества состояний, и инверсную населенность между какой-нибудь парой уровней получить сложно. Также немаловажным обстоятельством, существенно повышающим эффективность химических реакций, является возможность осуществления так называемых цепных реакций, когда один из продуктов реакции может повторно вступать в химическую реакцию, приводящую к образованию возбужденной молекулы активной среды, например: A+B2→AB*+B A2+B→AB*+A и т. д. Перейдем к рассмотрению конкретных представителей химических лазеров. В HF-лазере инверсная населенность возникает между колебательными уровнями молекулы HF при реакции замещения между атомарным фтором и молекулой водорода, находящимися в газовой фазе: F+H2→HF*+H. (22.1) В результате этой реакции выделяется теплота приблизительно 32 ккал/моль, причем приблизительно 70% от нее идет на возбуждение колебательных состояний фторида водорода. Заселенными оказываются 2-й и 3-й колебательные уровни основного электронного состояния. Вследствие различий в скоростях термодинамической релаксации разных колебательных состояний в течение определенного периода времени населенность 2-го колебательного уровня приблизительно в 3 раза превышает населенность 1-го уровня, то есть на переходе 2→1 возникает большая инверсная населенность. Еще большее количество теплоты (98 ккал/моль) выделяется в реакции атомарного водорода и молекулярного фтора: F2+H→HF*+F. (22.2) При этом в молекуле HFвозбуждаются колебательные уровни вплоть до 10-го. В реальном лазере реакции (22.1) и (22.2) протекают одновременно, и атомы фтора и водорода, образующиеся в одной из реакций, далее принимают участие в другой реакции. В итоге генерация происходит на нескольких колебательных переходах в диапазоне уровней от 1-го до 6-го в спектральном диапазоне от 2.7 мкм до 3.3 мкм. Характер генерации при этом практически такой же, что и в газовом CO-лазере: наблюдается колебательно-вращательная структура, каскадная генерация, генерация на основной частоте и на обертоне, могут реализовываться условия для частичной инверсии между соседними колебательными уровнями (инверсия достигается между некоторыми вращательными состояниями соседних колебательных уровней, и генерация тогда возникает на линиях P-ветви). Вообще говоря, процессы релаксации возбужденных состояний в HF-лазере (равно как и в других молекулярных химических лазерах) аналогичны рассмотренным ранее процессам для молекулярных лазеров, работающих на колебательных переходах – происходят процессыVV-обмена иVT-релаксации, в возбужденных колебательных состояниях очень быстро устанавливается равновесное распределение по вращательным состояниям. Способы получения исходных компонентов для начала химических реакций могут быть разными. Например, атомарный фтор может быть получен при столкновениях молекулы SF6(или NF3, UF6) с электроном в электрическом разряде. Можно использовать также в исходной смеси молекулярные фтор и водород, диссоциация которых на атомы происходит в результате облучения УФ излучением: H2(F2)+h→2H(F). (22.3) Однако использование смеси, состоящей только из молекул фтора и водорода, нежелательно вследствие ее высокой взрывоопасности. Поэтому в исходные газовые смеси обычно добавляется молекулярный кислород. В качестве источников УФ излучения можно использовать различные УФ лампы (например, кварцевые), а также искровые разряды. Эффективность УФ диссоциации выше по сравнению с использованием электрического разряда, однако в последнем случае удается достигать заметно более коротких времен диссоциации (диссоциация исходной смеси в электрическом разряде возможна за времена порядка наносекунд, тогда как при УФ диссоциации это происходит за микросекунды). Поэтому электрический разряд используется, как правило, в импульсных лазерах, а УФ воздействие чаще применяется для обеспечения работы лазера в непрерывном режиме. HF-лазер отличается большими величинами энергосъема с единицы объема активной среды – сотни джоулей с литра при атмосферном давлении газовой смеси. Наряду с HF-лазером, сходные характеристики имеют DF-, HCl, HBr-, DF-лазеры, перекрывающие ближний ИК диапазон в области длин волн 3.5 - 5 мкм. Наибольшая выходная мощность получена в DF-лазере – до нескольких МВт в непрерывном режиме. Еще одним примером химического лазера является фотодиссоциационный йодный лазер, в котором инверсная населенность в атомарном йоде достигается в реакции фотолиза молекулы CF3I: CF3I+h→I*+CF3. (22.4) В результате этой реакции йод образуется в состоянии 2P1/2, откуда релаксирует в состояние2P1/2с испусканием фотона на длине волны 1.315 мкм. Источником излучения для этой реакции могут служить немонохроматические кварцевые лампы, поскольку поглощение проходит в широкой спектральной полосе, обусловленной множеством энергетических состояний молекулыCF3I, имеющей большое количество колебательных степеней свободы. Также могут использоваться открытые разряды. Вследствие наличия релаксационных процессов реакция фотодиссоциации должна протекать быстро. Поэтому накачка включается в импульсном режиме. Основным достоинством данного лазера является возможность обеспечения фотодиссоциации больших объемов CF3I, что приводит к высоким величинам энергосъема. Кроме молекулы CF3I, могут использоваться молекулыC3F7I иCH3I. Еще одним примером химического лазера является DF-CO2лазер, излучающий на тех же самых переходах, что и рассмотренный ранееCO2лазер. Однако в данном случае механизм создания инверсной населенности принципиально иной и состоит в прохождении следующей последовательности реакций: Сначала смешиваются молекулы оксида азота и фтора, в результате чего происходит образование атомарного фтора: NO+F2→NOF+F. (22.5) Далее фтор взаимодействует с молекулярным дейтерием, и происходит образование молекулы DFв возбужденном колебательном состоянии: F+D2→DF*+D. (22.6) Образовавшийся атом дейтерия может провзаимодействовать с непрореагировавшим в реакции (22.5) молекулярным фтором также с образованием возбужденной молекулы DF: D+F2→DF*+F. (22.7) Наконец, на последней стадии к DFподмешивается двуокись углерода, и в результате резонансной передачи энергии заселяется верхний лазерный уровеньCO2: DF*+CO2→DF+CO2*. (22.8) На слайде приведена конструкция такого лазера. На выходе проточной емкости, в которой происходят химические реакции, устанавливаются зеркала резонатора лазера. Эта схема близка к схеме газодинамического лазера с поперечным протоком активной среды. Мощность этого лазера может достигать нескольких сотен ватт при расходе веществ порядка одного грамма в секунду. Основной интерес к химическим лазерам обусловлен следующими обстоятельствами. 1. Сам по себе механизм накачки, заключающийся в непосредственном преобразовании энергии химической реакции в энергию электромагнитного поля является интересным. 2. Большие количества энергии, выделяющейся в результате экзотермической химической реакции, приводят к большим мощностям излучения химических лазеров. Существенным недостатком химических лазеров является сложность устройства, а также взрывоопасность химических реагентов и их высокая токсичность. 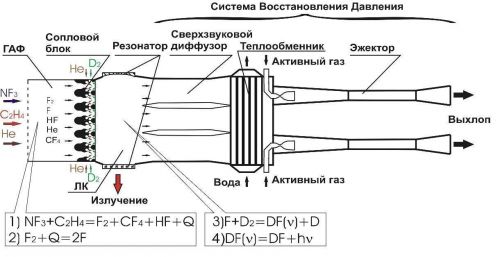 БИЛЕТ 4. 1.     2. К числу наиболее простых для изучения случайных процессов относятся стационарные случайные процессы у которых все вероятностные характеристики не зависят от времени. В частности, у стационарного случайного процесса математическое ожидание и дисперсия из функций аргумента t превращаются в константы: Это означает, что все сечения стационарного случайного процесса имеют одинаковое математическое ожидание и дисперсию (рис.6.4). 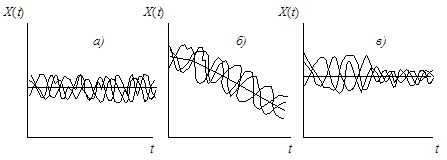 Рис.6.4. Реализации стационарного (а) и нестационарных (б,в) случайных процессов; б – нестационарность по математическому ожиданию; в – нестационарность по дисперсии. Различают стационарные случайные процессы в узком смысле и в широком смысле. Случайный процесс называется стационарным в узком смысле, если его n-мерная плотность распределения не изменится при сдвиге всех его временных аргументов на одинаковую произвольную величину q. Поясним это на примере двумерной плотности распределения. Если стационарный случайный процесс X(t) имеет двумерную плотность f(t1, t2, x1, x2), то она не изменится если заменить t1 на t1+ q, а t2на t2 +q. Это означает, что плотность распределения стационарного случайного процесса не зависит от того в какие моменты t1 и t2 рассматриваются сечения, а зависит от расстояния между этими сечениями t1 – t2 = t. Случайный процесс называется стационарным в широком смысле, если его математическое ожидание постоянно (mx = conct), а корреляционная функция – есть функция сдвига между аргументами: Kx(t1, t2) = kx(t). Если стационарный случайный процесс является стационарным в узком смысле, то он является стационарным и в широком смысле (обратное утверждение не всегда верно). Корреляционная функция стационарного случайного процесса обладает следующими свойствами: 1. Она является четной функцией своего аргумента 2. Значение корреляционной функции стационарного случайного процесса при нулевом сдвиге t равно дисперсии случайного процесса 3. Помимо корреляционной функции используется нормированная корреляционная функция стационарного случайного процесса, которую также называю автокорреляционной функцией: Она обладает практически теми же свойствами, что и корреляционная функция, у которой изменен масштаб по оси ординат: 1. 2. 3. 3. Итак, дисперсия света – это зависимость показателя преломления вещества от частоты световой волны . Эта зависимость не линейная и не монотонная. Области значения ν, в которых
соответствуют нормальной дисперсии света(с ростом частоты ν показатель преломления n увеличивается). Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света, и в этой области частот наблюдается нормальная дисперсия света в стекле. На основе явления нормальной дисперсии основано «разложение» света стеклянной призмой монохроматоров. Дисперсия называется аномальной, если
т.е. с ростом частоты ν показатель преломления n уменьшается. Аномальная дисперсия наблюдается в областях частот, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла в инфракрасной и ультрафиолетовой частях спектра наблюдается аномальная дисперсия. Зависимости n от ν и λ показаны на рис. 10.4 и 10.5.
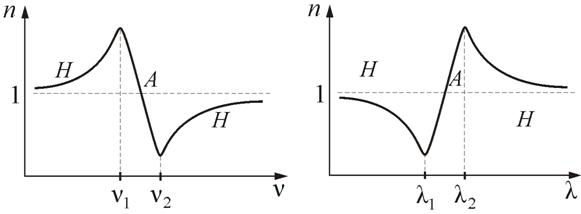 В зависимости от характера дисперсии групповая скорость u в веществе может быть как больше, так и меньше фазовой скорости υ (в недиспергирующей среде u=v). Групповая скорость u связана с циклической частотой ω и волновым числом k соотношением: , где w=2пυ, . Тогда 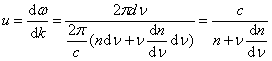 . Отсюда можно записать:
Таким образом, при нормальной дисперсииu < υ и . При аномальной дисперсии u > υ, и, в частности, если, то u > c. Этот результат не противоречит специальной теории относительности. Понятие групповой скорости правильно описывает распространение только такого сигнала (волнового пакета), форма которого не изменяется при перемещении сигнала в среде. (Строго говоря, это условие выполняется только для вакуума, т.е. в недиспергирующей среде). В области частот, соответствующих аномальной дисперсии, групповая скорость не совпадает со скоростью сигнала, так как вследствие значительной дисперсии форма сигнала так быстро изменяется, что не имеет смысла говорить о групповой скорости. |
