Механика сплошных сред. Цель работы рассчитать величины и оценить закономерности распределения компонент напряжений и смещений в окрестности незакрепленной горной выработки кругового очертания, расположенной в изотропном линейноупругом массиве. Исходные данные
 Скачать 184.11 Kb. Скачать 184.11 Kb.
|
ВведениеДо проведения выработки горный массив находится в состоянии устойчивого равновесия и его напряженное состояние определяется в общем случае силами тяжести горных пород. Раскрытие подземной выработки связано с удалением из нее породы, которая воспринимала давление пород, залегающих непосредственно над выработкой, и предотвращала смещения частиц породы на ее контуре. В связи с этим вокруг выработки возникает концентрация напряжений: стены выработки подвергаются повышенному давлению, а в кровле возникают растягивающие напряжения, достигающие иногда значительных размеров. Форма поперечного сечения выработок устанавливается в соответствии с физико-механическими свойствами пород и состояния пород, по которым они проводятся, величины и направления горного давления, срока службы и принятой конструкции крепи. Если выработку не крепят, ей придаётся форма поперечного пересечения, которая приближается к форме свода естественного равновесия. Круглая форма наиболее подходит при наличии всестороннего давления . В этом случае выработки крепят сборными железобетонными элементами, бетоном или металлическим креплением. Углеспускные скважины могут вообще не крепиться. Если один из компонентов горного давления значительно больше других, используется эллипсоидное сечение . Формулировка заданияЦель работы: рассчитать величины и оценить закономерности распределения компонент напряжений и смещений в окрестности незакрепленной горной выработки кругового очертания, расположенной в изотропном линейно-упругом массиве. Исходные данные: Рассчитать компоненты напряжений σR, σθ, σz и τRθ в изотропном упругом массиве пород на контуре и в окрестности незакрепленной выработки кругового очертания при коэффициентах бокового распора λ=1 и λ=λ2. Для этих же условий рассчитать величины смешений контура выработки ur и uθ. Для построения эпюр при λ=λ2 рассмотреть направления с угловой координатой θ=0, 45 и 900. Безразмерный радиус r=R/R0 (R – текущий радиус; R0 – радиус выработки) принимать в диапазоне от 1 до 12 (не менее 10 точек). Таблица 1. Исходные данные
Решение заданияВ рамках данного расчетно-графического задания предполагается использование линейно-упругой модели массива пород. Для этой модели коэффициент бокового распора следует определять согласно гипотезе Динника: где Для определения компонентов напряженного состояния в окрестности горной выработки воспользуемся решением задачи Кирша из теории упругости: Смещения точек массива в окрестности горной выработки следует определять по следующим формулам: 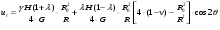 , (5) , (5)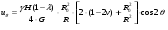 , (6) , (6)где Пользуясь формулами (1), (2), (3), (4), (5), и (6) выполняем расчет всех величин и построения эпюр. Выполняем расчеты и построение эпюр распределения ненулевых компонент напряжений для случая λ=1. При Таблица 2. Результаты вычислений напряжений при
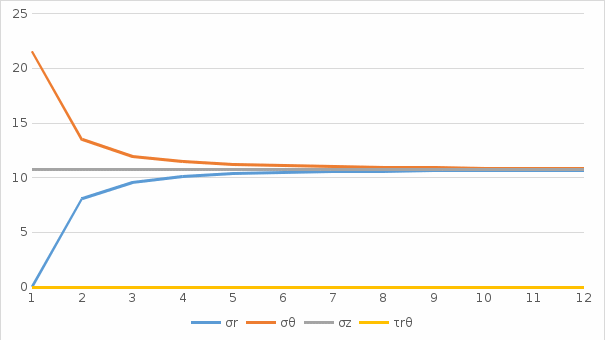 Рисунок 1 – Эпюра напряжений при Выполняем расчеты построение эпюры распределения нормальных тангенциальных напряжений на контуре незакрепленной горной выработки кругового очертания для случая λ=1. Таблица 3. Результаты вычислений нормальных тангенциальных напряжений на контуре (при r=1)
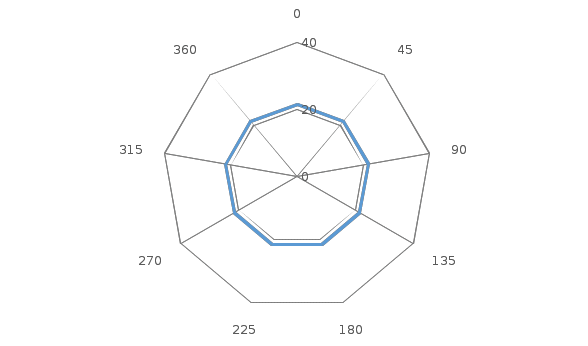 Рисунок 2 – Эпюра нормальных тангенциальных напряжений на контуре Выполняем расчеты и построение эпюр распределения смещений породного контура выработки кругового очертания для случая λ=1. Таблица 4. Результаты вычислений смещений контура (при r=1)
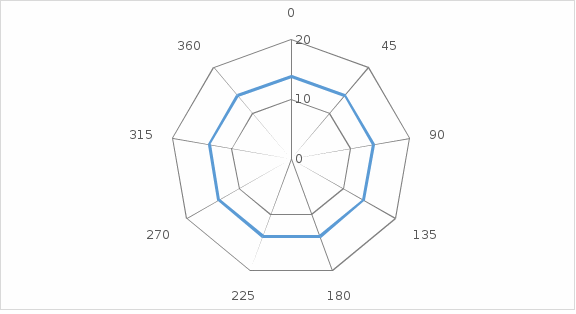 Рисунок 3 – Эпюра смещений ur контура при Выполняем расчеты и построение эпюр распределения ненулевых компонент напряжений для направлений с угловой координатой θ=0, 45 и 900 для случая λ= λ2. Таблица 5. Результаты вычислений напряжений при
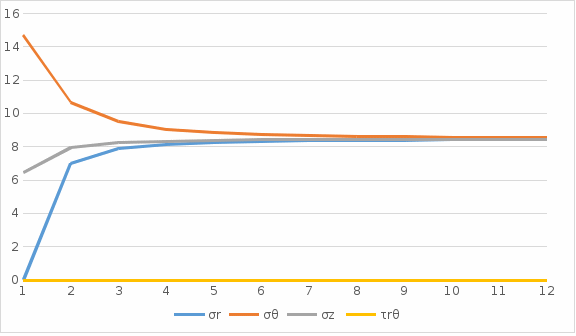 Рисунок 4 – Эпюра напряжений при Таблица 6. Результаты вычислений напряжений при
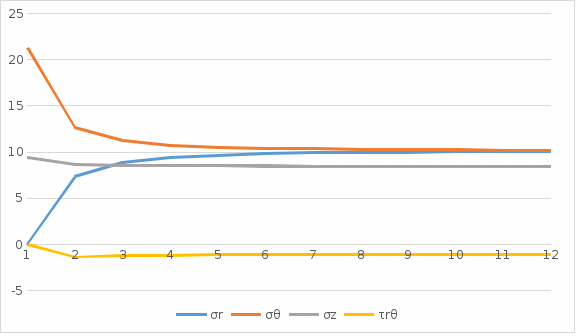 Рисунок 5 – Эпюра напряжений при Таблица 7. Результаты вычислений напряжений при
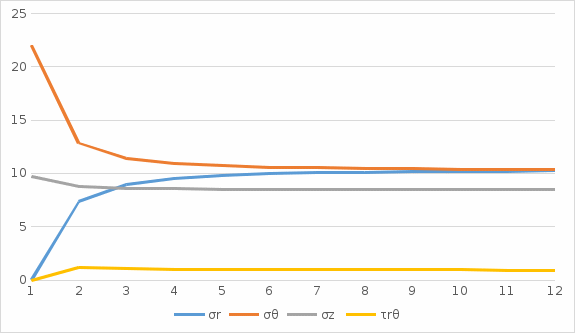 Рисунок 6 – Эпюра напряжений при Выполняем расчеты и построение эпюры распределения нормальных тангенциальных напряжений на контуре незакрепленной горной выработки кругового очертания для случая λ= λ2. Таблица 8. Результаты вычислений нормальных тангенциальных напряжений на контуре (при r=1)
Для наглядности совмещаем эпюры распределения нормальных тангенциальных напряжений на контуре незакрепленной горной выработки кругового очертания для двух случаев при 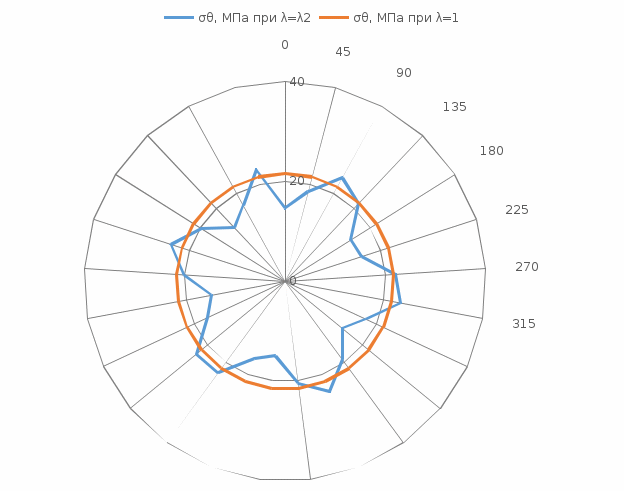 Рисунок 7 – Эпюра нормальных тангенциальных напряжений на контуре при Выполняем расчеты и построение эпюр распределения смещений породного контура выработки кругового очертания для случая λ= λ2. Таблица 9. Результаты вычислений смещений контура (при r=1) λ= λ2 и значениях
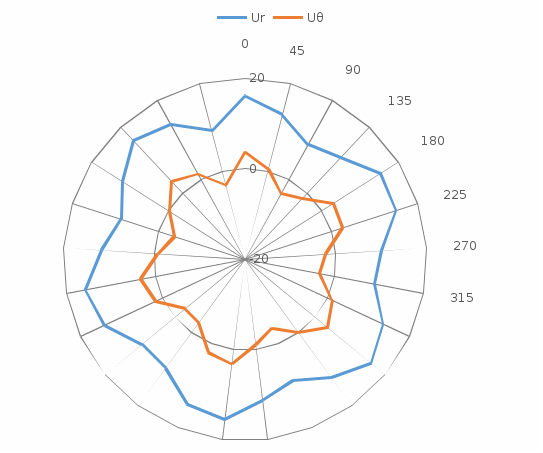 Рисунок 8 – Эпюра смещений ur и uθ контура при λ= λ2 и значениях Вывод: В ходе выполнения данной расчетно-графической работы был выполнен расчет параметров напряженно-деформированного состояния массива горных пород: рассчитаны компоненты напряжений в изотропном упругом массиве пород на контуре и в окрестности незакрепленной выработки кругового очертания, а также рассчитаны величины смещений контура незакрепленной горной выработки круглого очертания, расположенной в изотропном линейно-упругом массиве. Для графического представления данных о распределении соответствующих величин напряжений и смещений на контуре и в окрестности выработки в данной работе были построены эпюры. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
