Лекция. Ч3.К1.Лек.23 ув.граф.. Ч. 3 Колебания и волны радел колебания введение Колебания и их классификация
 Скачать 1.78 Mb. Скачать 1.78 Mb.
|
|
Ч.3 КОЛЕБАНИЯ И ВОЛНЫ Радел 1. КОЛЕБАНИЯ Введение: Колебания и их классификация Опр-е: К. называется процесс отклонения физической величины от положения равновесия в ту или другую сторону в той или иной последовательности. Обычно таковым считается всякий процесс с определённой степенью повторяемости. Периодические колебания – один из самых характерных видов К. Основная задача описания Кол. – определение колебательной функции x(t) с набором необходимых параметров. x(t) = x(t + nT), где Т – период, n – целое число. Классификация К. условна. По повторяемости процесса: а) периодические – одни и те же состояния системы повторяются через одинаковые промежутки; б) квазипериодические – степень повторяемости более низкая; система не всегда возвращается в исходное состояние; в) непериодические К. 2. По характеру воздействия: а) свободные (собственные) К. Нет внешних сил ( 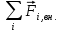 = 0) = 0)Делятся на: затухающие и незатухающие; б) вынужденные К. Причина их: 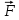 (t) – вынуждающая сила; (t) – вынуждающая сила;в) автоколебания Происходят в замкнутой системе с постоянным воздействием. 3. По изменению физ. параметров колеб. системы. а) линейные (параметры не зависят от ампл. А), б) нелинейные (например, Т = Т(А) ); в) параметрические (один из параметров периодически изменяется, например, ℓ = ℓ(t) ). 4. По виду колеб. функции а) гармонические, б) негармонические, в) прочие. Особую роль играют т.н. малые (линейные) колебания как наиболее простые. Сложные и нелинейные Кол. можно конструировать как комбинацию простых (гармонических) – Фурье разложение. ЛИТЕРАТУРА Жилинский А.П., Мискинова Н.А., Самодурова И.Д. Физика.ч.3. “Колебания” (конспект лекций), МТУСИ, 2004г. 2. Савельев И.В. “Курс общей физики” , т.1,2; стерео. 3. Т.И. Трофимова « Курс физики», 1990. 4. Детлаф А.А., Яворский Б.М., “Курс физики”; стерео. Гл.1 СВОБОДНЫЕ КОЛЕБАНИЯ § 1.1 Дифференциальные уравнения свободных колебаний Условием их реализации для системы является наличие: *) положения равновесия, **) возвращающей (квазиупругой) силы, ***) инерции. Наличие диссипативной силы приводит к затуханию К. 1.1.1. Случай механических систем Гармонический осциллятор (грузик на горизонтальной пружине) 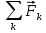 =m =m 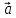 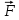 y + y + 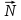 + m + m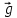 + + 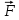 тр. = m тр. = m 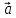 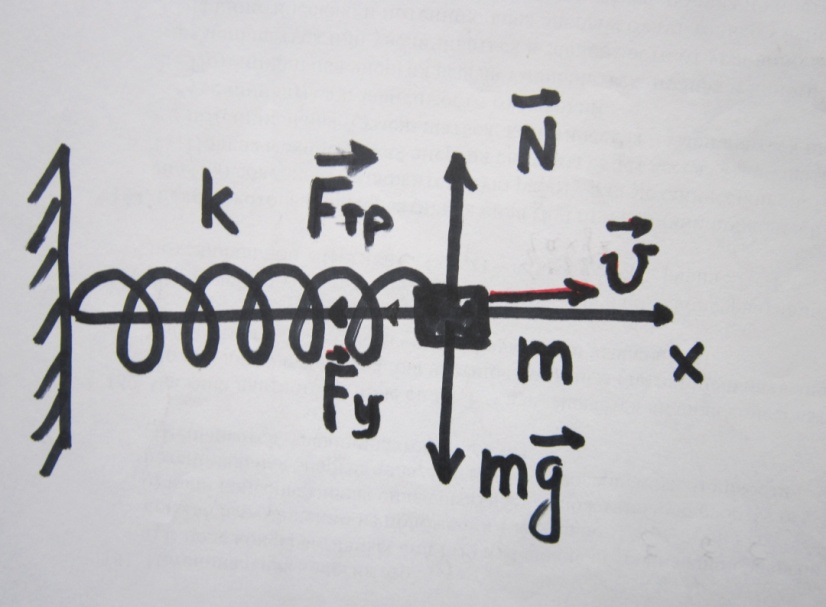 Запомним: 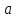 = = 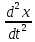 = = 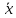 , Fy = - kx , Fy = - kx В координатной форме при отсутствии трения: По ОХ: m 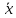 = Fy = FyИ соответственно: 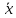 + + 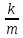 x = 0 x = 0 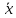 + ωo2 x = 0 (*) + ωo2 x = 0 (*)Здесь ωo2 = 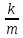 . . При наличии трения По ОХ: m 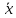 = Fy + Fтр. = Fy + Fтр.По ОУ: 0 = N + mg Пусть Fтр. = - r υ = - r 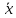 Тогда приходим к уравнению 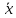 + 2δ + 2δ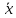 + ωo2 x = 0 , (**) + ωo2 x = 0 , (**)где δ = 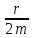 - называют коэфф. затухания. - называют коэфф. затухания.Физический маятник Массивное тело, характеризуется моментом инерции Iz и совершает вращательное движение относительно оси ОZ. Вращательный момент Мz = - Fтяж.∙ h = - mgl∙sin α 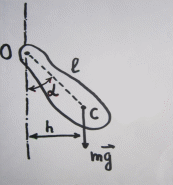 Уранение динамики Iz ∙ β = 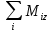 , где β - угловое ускорение, , где β - угловое ускорение, β = 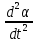 = = 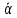 Если нет моментов сил трения Iz 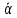 = - mgl∙sin α = - mgl∙ α (угол мал!) = - mgl∙sin α = - mgl∙ α (угол мал!)Или: 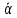 + + 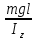 α = 0 α = 0
Здесь ωo2 = 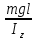 . .При наличии момента сил трения Мz,тр. = - γ 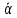 = - γ Ω, = - γ Ω,где 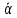 = Ω – угловая скорость движения = Ω – угловая скорость движения Имеем:
где δ = 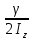 - называют коэфф. затухания. - называют коэфф. затухания.Свободные К. в электрическом контуре 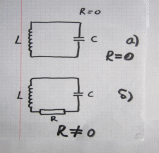 Согласно 2ому закону Кирхгофа 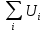 = = 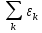 Т.к. в контуре действует ЭДС индукции, равная падению напряжения на ёмкости и сопротивлении R∙ I + 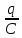 =- =- 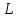 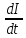 Поскольку 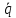 = I , = I , 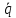 = = 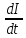 . Собрав в уравн-и слагаемые и поделив L, получим . Собрав в уравн-и слагаемые и поделив L, получим
Здесь δ = 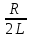 , ωo2 = , ωo2 = 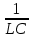 В случае идеального контура без сопротивления будем иметь 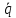 + ωo2 q = 0 , т.е. (*) + ωo2 q = 0 , т.е. (*)§ 1.2 Дифференциальное уравнение гармонических колебаний и его решение 1.2.1. Дифф. уравнение Итак, для рассмотренных нами колебательных систем, в случае отсутствия диссипативных сил получали типичные ур-я (*) как для мех. так и электр. систем
Это дифференциальное уравнение гармонических колебаний, где в качестве переменной выступали смещения (линейное x и угловое - α), заряд q и … точку не ставим. Уравнение 2го порядка, однородное, линейное. (Порядок – по старшей производной, однородное – родственники, линейное – первая степень переменной и её “деток”, “внуков”. Важна консервативность системы (нет сил трения, сопротивления) 1.2.2. Решение дифф. уравнения Способ 1 (подстановкой) Легко убедиться, что функции x1 (t) = A cos(ωоt + φo), x2 (t) = A sin(ωоt + φo), x3 (t) = A exp j(ωоt + φo) 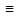 А А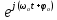 являются решением ур-я (1). являются решением ур-я (1). Здесь j = 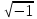 , А и φo – произвольные постоянные , А и φo – произвольные постоянныеЭто тем более понятно, что cos(α + β) = =cosα∙ cos β – sin α∙ sin β cos(ωоt + φo) = cos ωоt ∙A1 – A2 sin ωot, где A1 = cos φo , A2 = sin φo Итак: x1 (t) и x2 (t) гармонические функции, процесс движения – простейшие колебания. А – амплитуда, ωо - собственная частота, φo - начальная фаза, вся скобка (ωоt + φo) - фаза колебаний. Видим, что решение в комплексной форме удобно и эффективно. На практических уделите этому внимание. Отметим, что комплексное число Z= X +jY или Z = ρejα = ρcos α + jρ sin α, Z∙Z* = ρ2 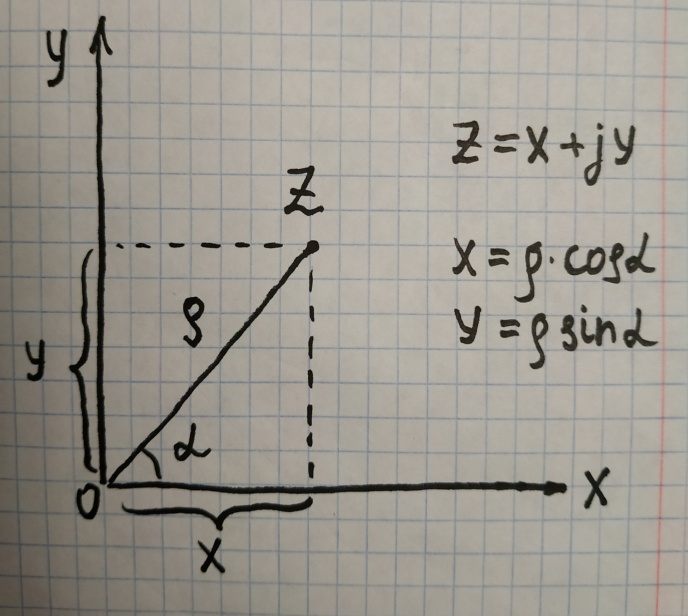 Заметим, что согласно Эйлеру: cos α = 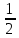 (е jα + е-jα) (е jα + е-jα)sin α = 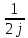 (е jα - е-jα) (е jα - е-jα)Способ 2 Решение ур.(1): 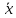 + ωo2 x = 0 + ωo2 x = 0 ищем как в теории дифф. ур-й в форме: x(t) = 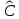 еλt, где еλt, где 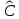 и λ – постоянные. Подставляя и λ – постоянные. Подставляя 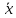 = λ = λ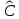 еλt и еλt и 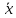 = λ2 = λ2 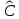 еλt , приходят к характеристическому ур-ю: еλt , приходят к характеристическому ур-ю:
Его корни мнимые: λ = 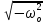 λ1 = + jωо , λ2 = - jωо λ1 = + jωо , λ2 = - jωоТогда x (t) = 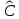 1 е λ1t + 1 е λ1t + 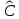 2 е λ2t и если взять 2 е λ2t и если взять 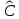 1 = 1 = 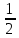 А еxp(jφo) А еxp(jφo) 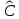 1 = 1 = 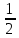 А еxp(-jφo), то решение примет вид А еxp(-jφo), то решение примет видx (t) = A cos(ωоt + φo), В качестве решения берут действительную часть комплексного числа. Таким образом решением дифф. ур. (1) будем считать ур-е гармонических колебаний:
Постоянные А и φo определяют пользуясь начальными значениями величин (смещения, скорости, ускорения, энергии). § 1.3 Дифф. ур-е затухающих колебаний. Его решение а) Квазипериодический (квазигармонический) режим: δ- мало! В наших примерах движения разных систем при наличии сил трения получали ур-я типа (**)
Это дифф. ур-е 2го порядка, линейное и однородное. Его решение ищем в виде: x(t) = 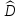 est и после подстановки производных в (1.3) приходят к характеристическому уравнению est и после подстановки производных в (1.3) приходят к характеристическому уравнениюs2 + 2 δ s + ωo2 = 0 Для случая δ ωо его корни: s1,2 = - δ 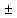 j j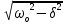 Введём обозначение ωз 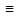 ω = ω = 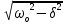 Решение (1.3) x(t) = 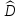 1 е- δt e jωt + 1 е- δt e jωt + 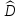 2 е- δt e -jωt = 2 е- δt e -jωt = =Ao е- δt cos(ωt + φo) При этом для коэффициентов справедливо: 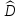 1 = 1 =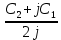 и и 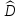 1 = 1 =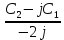 , , где С1 = Аcos φo и С2 = Аsin φo Итак, наше решение
носит название уравнения затухающих колебаний 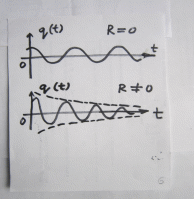 б) Случай δ ωо рассмотрим по возможности позже. Он характеризует сильное затухание, по сути релаксацию в апериодическом режиме. В принципе, бывает и сильнее затухание – критический режим. §1.4 Характерные параметры свободных З.Кол. 1*) Циклическая частота затух. К.
(здесь ω ωо ) период находят из Т = 2π/ω Т = 2π/ 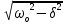 2*) Амплитуда затухающих колебаний уменьшается по экспоненциальному закону во времени
При t = 0 А = Ao 3*) Коэффициент затухания δ показывает убыль амплитуды в единицу времени: за t = 1c станет A = 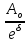 δ = 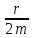 –для груза на пружине, –для груза на пружине, δ = 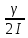 - физ. маятника, δ = - физ. маятника, δ = 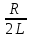 – эл. контура – эл. контура Большое разнообразие систем и параметров!!!! 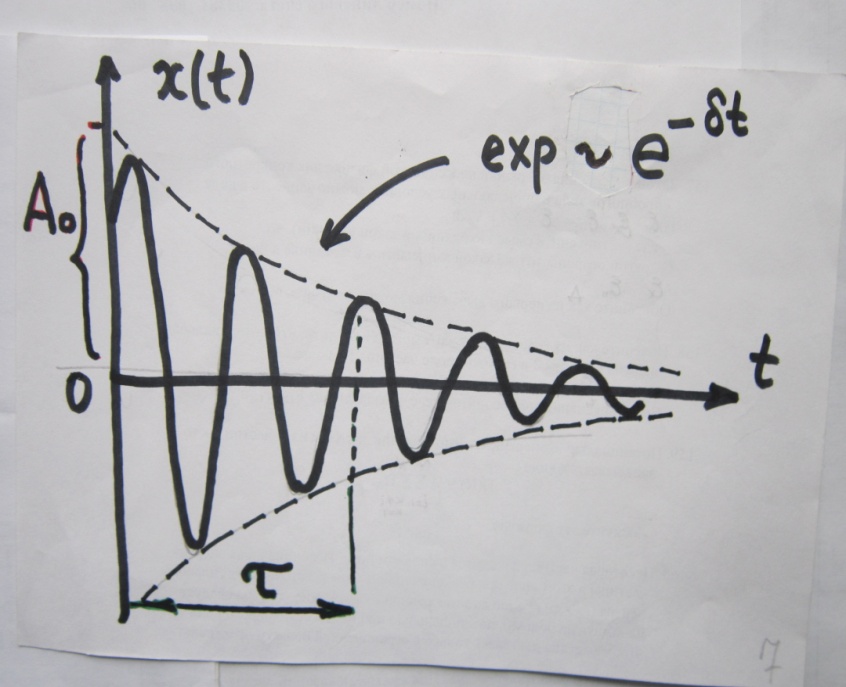 Легко видеть из (1.6):
4*) Время релаксации τ = 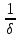 За этот промежуток амплитуда уменьшается в е раз Aτ = 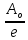 5*) Логарифмический декремент затухания 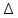 = = 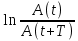 = δ∙Т = δ∙Т
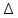 = = 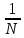 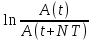 6*) Число колебаний за которое А уменьшается в е раз: Ne = 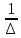 7*) Добротность системы θ = 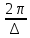 § 1.5 Апериодическое движение. Критический режим. Влияние начальных условий Это процесс движения, когда нет периодического движения. Разные ситуации. 1.5.1. Критический режим С ростом коэфф. затухания (δ → ωо) частота колебаний уменьшается (квазипериод растёт). При δ 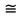 ωо имеем ω ωо имеем ω 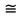 0 процесс превращается в релаксационный 0 процесс превращается в релаксационныйx(t) = Ao е- δt и носит название критического режима. 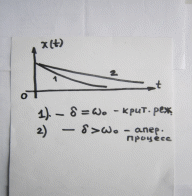 Этот вывод не совсем идеальный, т.к. не удовлетворяются начальные условия. Более глубокий анализ приводит к решению x(t) = xo + t ( 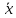 o + δxo) е- δt , o + δxo) е- δt ,включающему верхнее выражение для изменения смещения – см. рис. 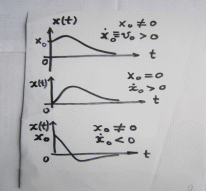 1.5.2. Апериодическое движение системы При δ ωо имеем две экспоненты с действительными показателями и процесс - явно не переодический x(t) = е- δt (D1 e ωt + D2 e -ωt ), где ω = 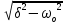 - вещественна. - вещественна.Особенность: затухание слабее, чем в критическом режиме. Наконец, случай δ 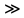 ωо ωо Силы инерции особой роли не играют, упругая сила уравновешивается силой трения x(t) = Ао 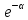 t , где α = t , где α = 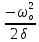 δ . δ .Ход кривой апериодического процесса, как и критического режима зависит от начальных условий – значений начального смещения и начальной скорости. § 1.6 Скорость и ускорение колебаний (1.6.1.). Энергия Кол. 1.6.1. Скорость гармонических колебаний Из ур-я (1.2), взяв производную по времени запишем υ кол. = 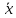 (t) (t) 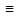 [ A сos(ωot + φo)]´ = [ A сos(ωot + φo)]´ == - A ωo sin(ωot + φo) = = A ωo cos(ωot + φo + 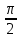 ) ) Вывод: Скорость опережает по фазе смещение на 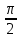 . .При t =0 называют: x(t =0) = xo = A сosφo – начальным смещением, 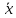 (t=0) = (t=0) =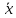 о = υо = A sin φo – начальной скоростью. о = υо = A sin φo – начальной скоростью. Ускорение гармонических колебаний Анологично, взяв вторую производную от x(t) по времени, 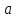 кол. = кол. = 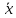 = -A ωo2 cos(ωot + φo) = = -A ωo2 cos(ωot + φo) = = A ωo2 cos(ωot + φo + π) Вывод: Ускорение опережает по фазе смещение на π и находится с ним противофазе. 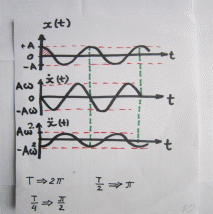 При t =0 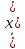 t=0) = t=0) =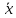 о = о =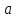 о = A сos φo – начальное ускорение о = A сos φo – начальное ускорениеЛегко видеть, что
Из основного тригонометрического тождества следует: Чтобы иметь однозначное решение нужно знать значения произвольных постоянных А и φo , которые определяются в момент времени называемый начальным.
1.6.2. Энергия свободных колебаний Энергия гармонических колебаний Рассмотрим идеальный электрический контур. Энергия э.п. конденсатора аналогична потенциальной энергии системы Пэ = Wэ = 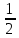 CU2 = CU2 = 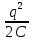 Энергия м.п. катушки анологична кинетической энергии системы. εк = Wм = 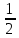 LI2 , I(t) = LI2 , I(t) = 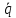 2 2 q(t) = qm cos(ωot + φo), 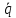 (t) = - qm ωo sin(ωot + φo), (t) = - qm ωo sin(ωot + φo), Тогда полная энергия К. W = Wэ + Wм = 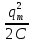 [cos2(…) + sin2 (…)] = const [cos2(…) + sin2 (…)] = const Cледует помнить: 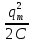 = = 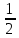 L L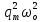 Т.к. cos2 (…) = 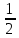 [1-cos 2(ωot + φo)], то очевидно, изменение электрической и магнитной энергии происходит с удвоенной частотой в противофазе. [1-cos 2(ωot + φo)], то очевидно, изменение электрической и магнитной энергии происходит с удвоенной частотой в противофазе.Аналогичные результаты в случае механических систем. Для грузика на пружине W = Wкин. + Wп = 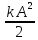 = = 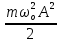 = const = const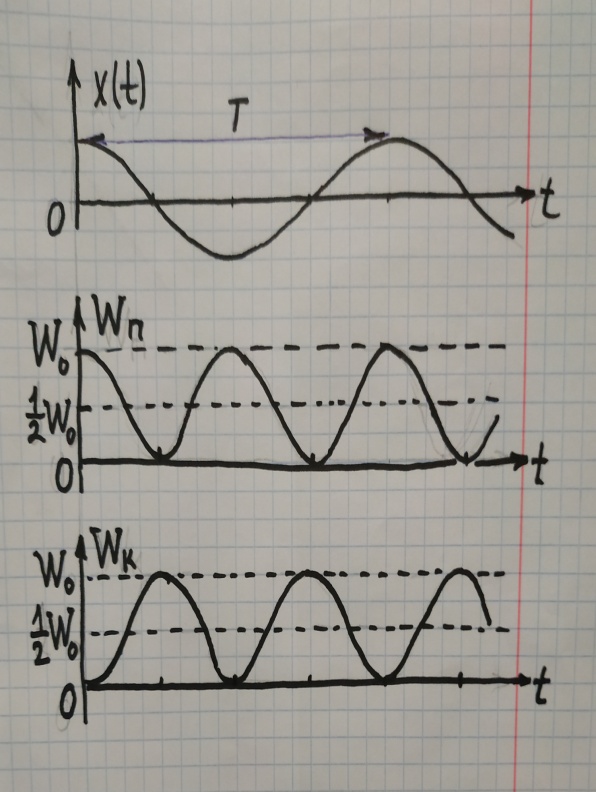 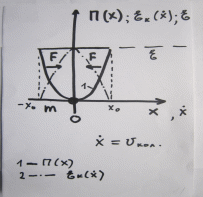 Энергия затухающих колебаний Амплитуда таких колебаний убывает во времени (зависит от t) На примере контура рассмотрим. W(t) = Wэ (t)+ Wм (t) q(t) = qm е- δt cos(ωt + φo), где ω = 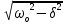 I(t) = 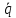 = - δ qm е- δt cos(ωt + φo) - = - δ qm е- δt cos(ωt + φo) - - ω qm е- δt sin (ωt + φo), При δ ωо (малое затухание) и пренебрегаем 1ым слагаемым. I(t) 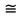 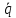 = - ω qm е- δt sin (ωt + φo), = - ω qm е- δt sin (ωt + φo), W(t) = 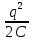 + + 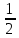 LI2 LI2 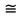 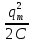 е- 2δt = е- 2δt = 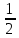 L L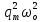 е-2δt = е-2δt = =Wо е- 2δt
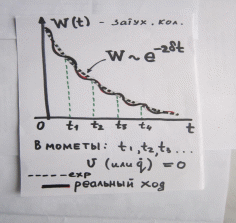 Заметим, что для энергии колебаний кофф. затухания в два раза больше! 1.6.3. Связь убыли энергии осциллятора и добротности системы Имеем для скорости изменения энергии 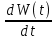 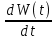 = -2Wо е- 2δt = -2Wо е- 2δt dW(t) = -2δ W(t)∙dt За время, равное периоду: dt = T и dW(t) 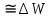 Тогда:│ 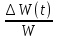 │= 2δ∙T = 2 │= 2δ∙T = 2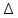 Т.к. добротность θ = 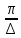 θ = θ = 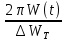 θ = 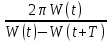
Это понятийное определение добротности системы: Она равна отношению энергии в данный момент к её изменению за период, умноженной на 2π § 1.7 Векторная диаграмма колебаний 1.7.1. В.Д. гармонического К. Уравнение x (t) = A cos(ωоt + φo) (1.2) 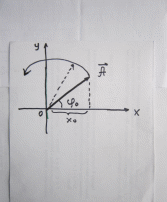 можно рассматривать как проекцию на ось Х зависящего от времени вектора 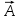 (t). Его модуль равен амплитуде Г.К. Вектор (t). Его модуль равен амплитуде Г.К. Вектор 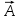 вращается против часовой стрелки относительно т. О с ростом времени. Начальная фаза φo определяет его положение в момент t=0 (см. рис.) вращается против часовой стрелки относительно т. О с ростом времени. Начальная фаза φo определяет его положение в момент t=0 (см. рис.)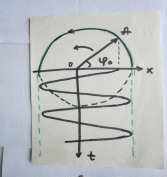 1.7.2. В.Д. затухающего квазигармонического К. Здесь отличие в том, что модуль вектора убывает во времени 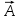 = = 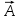 (t) = (t) = 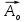 е- δt вместо окружности описывается концом вектора циклоида. Будем иметь обычное затухающее колебание в зависимости от t. е- δt вместо окружности описывается концом вектора циклоида. Будем иметь обычное затухающее колебание в зависимости от t.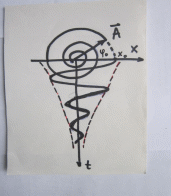 α φ 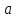 q q 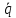 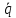 φo β ωо ω 2 π φo β ωо ω 2 π§ ℓ δ λ φ ε θ α π υ ν ω τ μ ψ ρ ∙ § ΄ 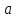 Мz Мz 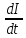 δ = 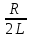 ωo2 = ωo2 = 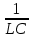 cos(ωt + φo) sin(ωt + φo) cos(ωt + φo) sin(ωt + φo)е- δt ω = 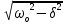 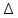 |

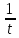
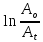 (1.7)
(1.7)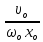 (1.9)
(1.9) 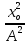 +
+ 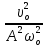 = 1 (1.10)
= 1 (1.10)