|
|
Оптика Компьютерная лабораторная работа. Дифр.решетка. Чайковский филиал
Министерство науки и Высшего образования российской федерации
Чайковский филиал
федерального государственного автономного
образовательного учреждения высшего профессионального образования
"Пермский национальный исследовательский политехнический университет"
(ЧФ ПНИПУ)
Кафедра автоматизации, информационных и инженерных технологий
Оптика
Компьютерная лабораторная работа №1
“Дифракционная решетка”
2020
ДИФРАКЦИЯ
1. Явление дифракции света.
В геометрической оптике широко пользуются понятием светового луча, т.е. узкого пучка света, распространяющегося прямолинейно. Границы тени на экране за непрозрачным препятствием определяются лучами света, которые проходят мимо препятствия, касаясь краев его поверхности.
В то же время прямолинейность распространения света не столь очевидна с позиций волновой теории Гюйгенса. Иначе говоря, волны должны огибать препятствия. Это происходит при освещении небольших непрозрачных препятствий или при прохождении света сквозь достаточно узкие щели и отверстия. В этом случае на экране, установленном позади препятствий или отверстий, вместо четко разграниченных областей света и тени наблюдается система максимумов и минимумов освещенности.
Все явления, связанные с огибанием световыми волнами препятствий и проникновением света в область геометрической тени, носят название дифракции света. Слово дифракция происходит от латинского слова diffractus - преломленный.
В более широком смысле дифракцией называют совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями его распространения от законов геометрической оптики.
Дифракционные явления присущи всем волновым процессам, но особенно отчетливо проявляются лишь в тех случаях, когда длины волн излучений сопоставимы с размерами препятствий. Так, звуковые волны хорошо слышны за углом дома, т.е. звуковая волна его огибает. Для наблюдения же дифракции световых волн необходимо создание специальных условий. Это обусловлено малостью длин световых волн (λ<1 мкм).
Как объяснить огибание световыми волнами препятствий и появление системы максимумов и минимумов освещенности вместо размытого изображения препятствия на экране? По принципу Гюйгенса каждая точка волновой поверхности является источником вторичных волн, распространяющихся вперед по всем направлениям, в том числе и в область геометрической тени препятствия. По идее Френеля появление максимумов и минимумов интенсивности является результатом интерференции лучей от большого числа вторичных (когерентных) источников (принципа Гюйгенса – Френеля).
2. Дифракция на дифракционной решетке
Р ассмотрим дифракцию на одномерной дифракционной решетке, так как этот вид дифракции находит широкое применение во многих методах спектрального анализа. ассмотрим дифракцию на одномерной дифракционной решетке, так как этот вид дифракции находит широкое применение во многих методах спектрального анализа.
Дифракционная решетка представляет собой систему большого числа одинаковых по ширине и параллельных друг другу щелей, лежащих в одной плоскости и разделенных непрозрачными промежутками, равными по ширине. Изготавливается путем нанесения параллельных штрихов на поверхность стекла с помощью делительных машин. Эти места являются, таким образом, практически непрозрачными промежутками между неповрежденными частями пластинки, которые играют роль щелей. Число штрихов на 1 мм определяется областью спектра исследуемого излучения и составляет от 300 мкм в инфракрасной области до 1200 мкм – в ультрафиолетовой области.
Итак, имеется система из N параллельных щелей с шириной каждой щели a и расстоянием между соседними щелями b (рис. 1). Сумма
a + b = d называется периодом, или постоянной дифракционной решетки. На решетку нормально падает плоская монохроматическая волна. Требуется исследовать интенсивность света, распространяющегося в направлении, составляющем угол φ с нормалью к плоскости решетки.
Кроме распределения интенсивности света вследствие дифракции на каждой щели, нужно учесть интерференцию между N пучками (перераспределение световой энергии за счет интерференции волн от N щелей - когерентных источников). Очевидно, минимумы будут на прежних местах, ибо условие минимума дифракции для всех щелей одинаково. Эти минимумы называются главными минимумами. Они соответствуют таким углам φ , для которых Аφ = 0, т.е. свет от разных частей каждой щели полностью гасится. В этом направлении ни одна щель не дает света. Условие главных минимумов 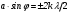 совпадает с условием (2.6). совпадает с условием (2.6).
К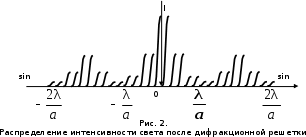
главным минимумам, создаваемым каждой щелью в отдельности, добавляются минимумы, возникающие в результате интерференции света, прошедшего через различные щели. Появляются добавочные минимумы в областях дифракционных максимумов. Внешне это проявляется в том, что широкие полосы, создаваемые одной узкой щелью, покрываются рядом более тонких полос, вызванных интерференцией лучей, исходящих от разных щелей: первой и второй, первой и третьей и т.д. Чем больше щелей, тем больше добавочных минимумов может возникнуть. Так как общий световой поток остается неизменным, происходит усиление световых потоков около направлений, удовлетворявших условиям максимумов при интерференции от разных щелей за счет уменьшения световой энергии в других направлениях. На рис. 2. для примера показано распределение интенсивности света и расположение максимумов и минимумов в случае двух щелей.
Воспользуемся методом Френеля. В одном и том же направлении все щели излучают свет совершенно одинаково. Результат интерференции зависит от оптической разности хода в сходственных точках двух соседних щелей до точки С-φ, на экране. Для всех сходственных точек эта разность хода одинакова и равна d sin φ. Если
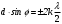 , (1) , (1)
то колебания от соседних щелей взаимно усиливают друг друга, и в точке С-φ наблюдается максимум дифракции. Амплитуда суммарного колебания в этих точках экрана максимальна:
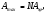 (2) (2)
где Aφ - амплитуда колебания, посылаемого одной щелью под углом φ. Интенсивность главного максимума
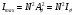 , (3) , (3)
поэтому формула (3) определяет положение главных максимумов интенсивности. Число k дает порядок главного максимума. Максимум нулевого порядка один и расположен в точке С0; максимумов первого, второго и т.д. порядков по два и расположены они симметрично относительно С0 , на что указывает знак "±".
Кроме главных максимумов, имеется большое число более слабых побочных максимумов, разделенных добавочными минимумами. Побочные максимумы значительно слабее главных максимумов. Расчет показывает, что интенсивность побочных максимумов не превышает 1/23 интенсивности ближайшего главного максимума. В главных максимумах амплитуда суммарного колебания в N раз, а интенсивность в N2 раз больше, чем в соответствующем месте дает одна щель. Увеличение максимумов происходит также за счет того, что в случае решетки отдельные яркие главные максимумы разделены темными областями добавочных минимумов и очень слабых побочных максимумов. В итоге происходит резкое сужение, дифракционных максимумов (пропорционально 1/N), которые становятся тонкими и яркими. Такие яркие линии, четко локализованные в пространстве, легко обнаруживаются и могут быть использованы для спектроскопических исследований.
По мере удаления от центра экрана интенсивность дифракционных максимумов убывает (увеличивается расстояние от источников). Поэтому не удается наблюдать все возможные дифракционные максимумы.
Заметим, что количество дифракционных максимумов, даваемых решеткой по одну сторону от центра экрана, определяется условием φ = π/2 - максимальный угол дифракции; sin φ < 1, откуда с учетом (3)
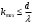 . (4) . (4)
При этом не следует забывать, что k - целое число.
Положение главных максимумов зависит от длины волны λ. Поэтому при освещении дифракционной решетки белым светом все максимумы, кроме центрального (k = 0), разложатся в спектр, обращенный фиолетовым концом к центру дифракционной картины. Таким образом, дифракционная решетка может служить для исследования спектрального состава света, т.е. для определения частот (или длин волн) и интенсивности всех его монохроматических компонент. Применяемые для этих целей приборы называются дифракционными спектрографами, если исследуемый спектр регистрируется с помощью фотопластинки, и дифракционными спектроскопами, если спектр наблюдается визуально.
3. Угловая дисперсия дифракционной решетки
Качество дифракционной решетки определяется двумя характеристиками: угловой дисперсией (D) и разрешающей силой (разрешающей способностью R).
Основное назначение дифракционной решетки - установление длины волны исследуемого излучения. Так как положение спектральных линий задается углом, определяющим направление лучей (см. уравнение (2.7)), целесообразно ввести угловую дисперсию D:
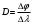 , (5) , (5)
где ∆φ - угловое расстояние между спектральными линиями, отличающимися по длине волны на ∆λ (рис.2.8); D - угловое расстояние между двумя линиями, отличающимися по длине волны на 1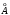 (1 (1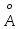 =10-10 м). =10-10 м).
Д ифференцируя (2.7) слева по φ, а справа по λ, находим, что ифференцируя (2.7) слева по φ, а справа по λ, находим, что 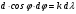 , откуда , откуда
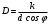 . (6) . (6)
Чем меньше период решетки d и чем выше порядок спектра k , тем больше угловая дисперсия. В пределах небольших углов (cos φ
1 ) можно положить
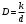 . (7) . (7)
Из выражения (7) следует, что угловая дисперсия прямо пропорциональна порядку дифракции k и обратно пропорциональна расстоянию между соседними штрихами (периодом решетки) d . Следовательно, для увеличения дисперсии необходимо увеличивать число штрихов на единицу длины. Этим объясняется необходимость изготавливать дифракционные решетки с возможно большим числом штрихов на 1 мм ее ширины.
4. Разрешающая сила дифракционной решетки
Б 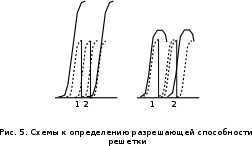 ольшая дисперсия оптических приборов (в том числе дифракционной решетки) является необходимым, но не достаточным условием для раздельного наблюдения двух близлежащих линий. В зависимости от крутизны кривой интенсивности соседние максимумы длин волн λ1 и λ2 могут наблюдаться как два самостоятельных или как один максимум. Как видно из рис. 5, при одинаковой угловой дисперсии линий λ1 и λ2 возможность их разрешения (раздельного восприятия) различна. Так, на рис. 5 слева минимум между линиями λ1 и λ2 , отсутствует, и эти линии не различаются как самостоятельные, а на рис. 5 справа имеются наблюдаемые минимумы между линиями λ1 и λ2. ольшая дисперсия оптических приборов (в том числе дифракционной решетки) является необходимым, но не достаточным условием для раздельного наблюдения двух близлежащих линий. В зависимости от крутизны кривой интенсивности соседние максимумы длин волн λ1 и λ2 могут наблюдаться как два самостоятельных или как один максимум. Как видно из рис. 5, при одинаковой угловой дисперсии линий λ1 и λ2 возможность их разрешения (раздельного восприятия) различна. Так, на рис. 5 слева минимум между линиями λ1 и λ2 , отсутствует, и эти линии не различаются как самостоятельные, а на рис. 5 справа имеются наблюдаемые минимумы между линиями λ1 и λ2.
Чтобы охарактеризовать способность прибора при данной дисперсии различать две близлежащие линии, вводится понятие разрешающей силы R. Для количественной характеристики этого понятия нужно ввести критерий разрешения. Согласно Рэлею, две близлежащие спектральные линии с равными интенсивностями и симметричными одинаковыми контурами разрешимы, если максимум одной длины волны λ1, совпадает с минимумом другой и наоборот. При удовлетворении этого условия интенсивность «провала» между максимумами составляет 80 % интенсивности каждой линии, что является достаточным для раздельного наблюдения линийλ1 и λ2. Нарушение критерия Рэлея приводит к наблюдению одной линии вместо двух.
Если разность длин волн | λ2 – λ1 | между двумя соседними максимумами, для которых выполняется критерий Рэлея, обозначить через ∆λ , а среднюю длину волны, соответствующую центру провала между максимумами, – через λ, то в качестве количественной характеристики разрешающей силы можно взять величину
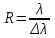 . (8) . (8)
Таким образом, разрешающей силой Rдифракционной решетки называется величина, обратная минимальной разности длин волн ∆λ (взятой около некоторой длины волны λ), которые разделены (разрешены) данной решеткой. Согласно условию Рэлея, а также (2.7) разрешение линий имеет место при
R = kN, (9)
где k- порядок дифракционного максимума; N - общее число щелей решетки.
Из выражения (9) видно, что чем больше число щелей решетки N , тем больше её разрешающая сила (разрешающая способность). При заданном числе щелей R увеличивается при переходе к спектрам высших порядков. Современные дифракционные решетки обладают довольно высокой разрешающей способностью (до 2×105 ).
Практическая часть
Проанализируем основные моменты компьютерной модели дифракционной решетки рис.1. По идее Френеля появление максимумов и минимумов интенсивности является результатом интерференции лучей от большого числа вторичных (когерентных) источников (принципа Гюйгенса – Френеля). Для компьютерной двумерной модели, каждую щель дифракционной решетки можно рассматривать как точечный источник вторичных волн (рис. 4). Таким образом, нам необходимо найти суммарную интенсивность света  линейно расположенных источников в точке линейно расположенных источников в точке  на экране. Кроме того, поскольку положение точки на экране. Кроме того, поскольку положение точки  на экране, пропорционально углу на экране, пропорционально углу 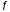 к прямой, перпендикулярной линии источников, то будем строить зависимость интенсивности непосредственно от угла к прямой, перпендикулярной линии источников, то будем строить зависимость интенсивности непосредственно от угла 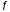 . Это позволяет исключить несущественные подробности моделирования работы дифракционной решетки. . Это позволяет исключить несущественные подробности моделирования работы дифракционной решетки.
Пусть имеется  гармонических осцилляторов, колеблющихся с частотой гармонических осцилляторов, колеблющихся с частотой 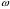 , расположенных на равных расстояниях один от другого и обладающих равными амплитудами , расположенных на равных расстояниях один от другого и обладающих равными амплитудами 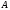 . Пусть разность фаз между осцилляторами составляет фазовый угол . Пусть разность фаз между осцилляторами составляет фазовый угол 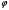 . Разность фаз создается либо из-за выбора фазовых сдвигов колебаний осцилляторов, либо потому, что мы находимся под углом к линии осцилляторов. Независимо от причин возникновения фазового сдвига нам надо вычислить сумму такого вида . Разность фаз создается либо из-за выбора фазовых сдвигов колебаний осцилляторов, либо потому, что мы находимся под углом к линии осцилляторов. Независимо от причин возникновения фазового сдвига нам надо вычислить сумму такого вида
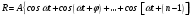 . (1) . (1)
Из справочника, находим сумму ряда (1)
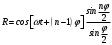 . (2) . (2)
Отношение
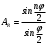 , (3) , (3)
очевидно, дает результирующую фазу амплитуду колебаний, как функцию фазового сдвига и количества источников. Поскольку непосредственно регистрируется приборами и, в частности, глазом не величина поля, а его интенсивность 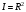 , то для амплитуды интенсивности пишем , то для амплитуды интенсивности пишем
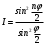 . (4) . (4)
Вид функции интенсивности исследуем, построив компьютерный график. Используя базовую программу построения графиков функций, пишем программу.
Объявляем переменные
tt,{шаг счета}
k,{число осцилляторов}
f,{разность фаз между осцилляторами}
Int{суммарная интенсивность}
: real;
Записываем блок построения графика
tt:=0.0001; {шаг счета}
k:=5; {число осцилляторов}
f:=0.0001; {сдвиг фаз между соседними осцилляторами, градусы}
For i:=1 to 200000 do
begin
Int:=Sqr(sin(0.5*k*f))/Sqr(sin(0.5*f)); {вычислениеинтенсивности}
SetPixel(X0+round(f*40*MasX),Y0-round(Int*40*MasY), clNavy); {вправо}
SetPixel(X0-round(f*40*MasX),Y0-round(Int*40*MasY), clNavy); {влево}
f:=f+tt;
end;
Пример работы программы приведен на рис. 1.
Задание.
1. Напишите и программу.
2. Осуществите отладку программы.
3. Протестируйте правильность работы программы, используя тот факт, что при одном осцилляторе выражение (4) составит 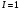 , а при двух осцилляторах , а при двух осцилляторах 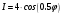 . .
Дайте ответ на следующие вопросы, используя компьютерный эксперимент.
1. Как ведет себя функция интенсивности при увеличении количества осцилляторов? Ответ проиллюстрируйте графиками.
2. От чего зависит количество дополнительных минимумов?
3. Что будет если число осцилляторов будет стремится к бесконечности?
4. При каких значениях разности фаз образуются главные максимумы? (кратно 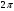 ) )
5. При каких значениях разности фаз образуются добавочные минимумы? (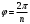 1 минимум) 1 минимум)
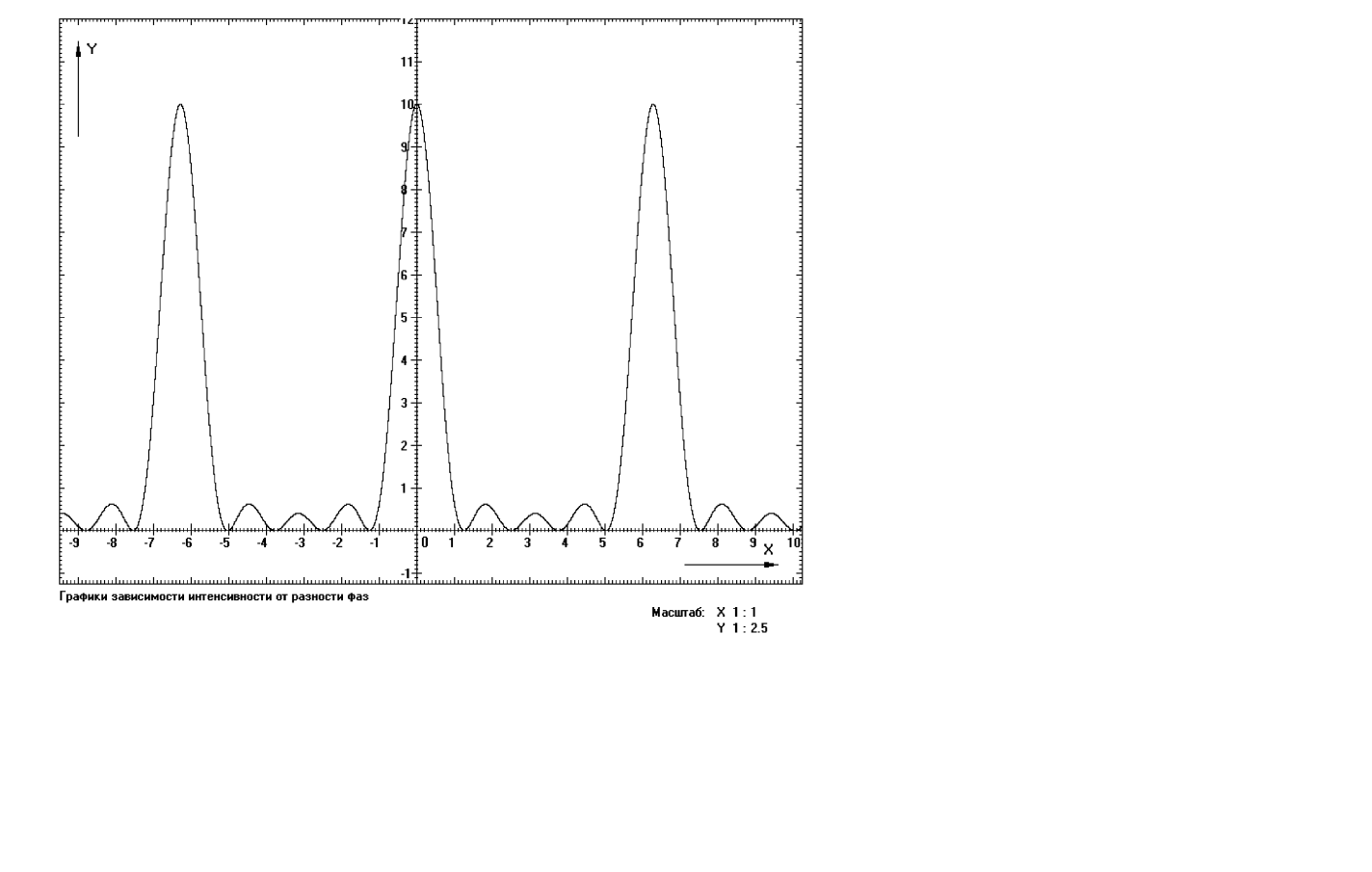
Рис.1. Зависимость интенсивности света от разности фаз между осцилляторами
Т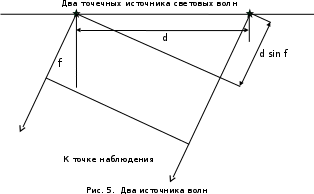
еперь смоделируем работу дифракционной решетки. Для этого нам необходимо определить разность фаз двух точечных осцилляторов расположенных на расстоянии 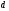 друг от друга. В нашем приближении мы пренебрегаем шириной источников осцилляторов. Как видно из рисунка 2, разность фаз волн обоих источников равна числу волн заключенных на отрезке друг от друга. В нашем приближении мы пренебрегаем шириной источников осцилляторов. Как видно из рисунка 2, разность фаз волн обоих источников равна числу волн заключенных на отрезке 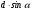 , умноженному на , умноженному на 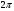 . Поэтому разность фаз двух источников равна . Поэтому разность фаз двух источников равна
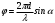 .. (5) .. (5)
Подставляя разность фаз в выражение (4) получим зависимость интенсивности от угла наблюдения
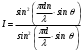 . .
Доработаем имеющуюся у нас программу интенсивности. Объявляем тип переменных.
tt, {шаг счета}
k, {число осцилляторов или число щелей ршетки}
f, {сдвиг фаз между осцилляторами}
a, {угол наблюдения}
d, {расстояние между щелями или период решетки}
L, {длина волны света}
Int {суммарная интенсивность}
: real;
Расширяем блок построения графика интенсивности.
{Блок расчета зависимости интенсивности света от угла наблюдения
после прохождения дифракционной решетки}
tt:=0.00001; {шаг счета}
k:=20; {число осцилляторов или щелей решетки}
d:=0.001/300; {период решетки в метрах (300 трихов на миллиметр)}
L:=575/1000000000; {длина волны в метрах, зеленый свет}
a:=0.0001; {угол, радианы}
For i:=1 to 200000 do
begin
f:=(2*Pi*d/l)*sin(a); {вычисление разности фаз источников}
Int:=Sqr(sin(0.5*k*f))/Sqr(sin(0.5*f)); {вычисление интенсивности}
SetPixel(X0+round(f*40*MasX),Y0-round(Int*40*MasY), clGreen); {вправо}
SetPixel(X0-round(f*40*MasX),Y0-round(Int*40*MasY), clGreen); {влево}
a:=a+tt; {изменение угла наблюдения}
end;
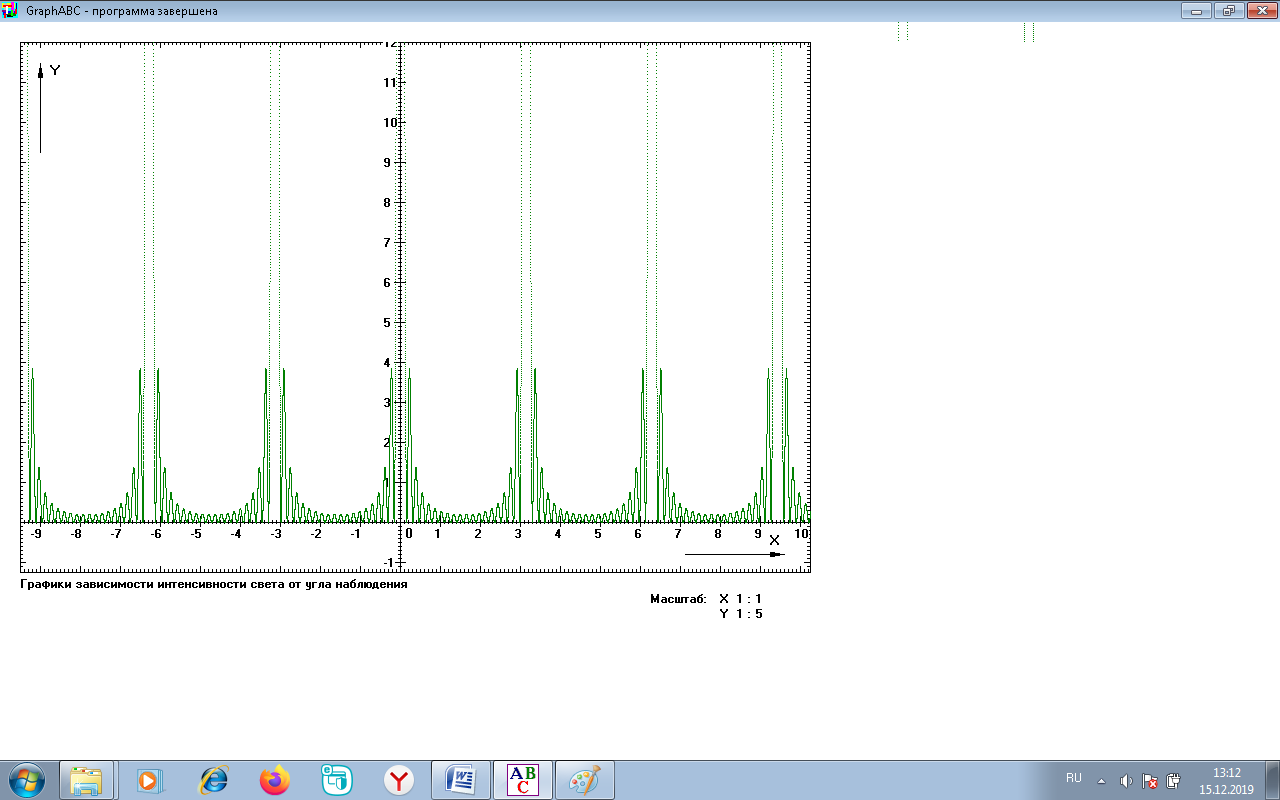
На рисунке 3 приведен график зависимости интенсивности света от угла наблюдения после прохождения дифракционной решетки.
Дайте ответ на следующие вопросы, используя компьютерный эксперимент.
1. Как расположены максимумы света различных длин волн относительно друг друга? Ответ проиллюстрируйте графиками, наложив друг на друга графики.
2. Пусть 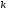 число щелей решетки. Сколько добавочных минимумов возникает между основными максимумами. число щелей решетки. Сколько добавочных минимумов возникает между основными максимумами.
3. С увеличением числа щелей интенсивность основных максимумов растет. Как она растет? Пусть число щелей увеличились в 3 раза. Во сколько раз возрастет интенсивность основных максимумов.
Напишите отчет о проделанной работе.
Н
Рис. 3 Интенсивности света от угла наблюдения
апишите отчет о проделанной работе.
ПРИЛОЖЕНИЕ
Длина световых волн
Длина волны
нм 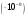
|
Частота
ТГц 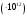
|
Цвет спектра
|
Длина
спектра
нм
|

|
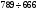
|
Фиолетовый
|

|

|
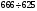
|
Синий
|

|

|
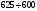
|
Голубой
|

|

550
|
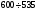
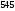
|
Зелёный
Max чувств для глаза
|

|

|
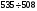
|
Жёлтый
|

|

|
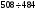
|
Оранжевый
|

|

|
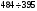
|
Красный
|

| |
|
|
 Скачать 285.03 Kb.
Скачать 285.03 Kb. ассмотрим дифракцию на одномерной дифракционной решетке, так как этот вид дифракции находит широкое применение во многих методах спектрального анализа.
ассмотрим дифракцию на одномерной дифракционной решетке, так как этот вид дифракции находит широкое применение во многих методах спектрального анализа. 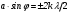 совпадает с условием (2.6).
совпадает с условием (2.6). 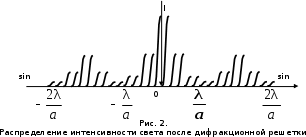
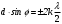 , (1)
, (1)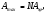 (2)
(2)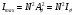 , (3)
, (3)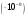
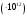
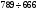
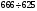
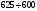
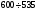
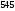
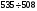
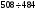
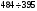

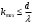 . (4)
. (4)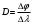 , (5)
, (5)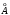 (1
(1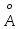 =10-10 м).
=10-10 м).  ифференцируя (2.7) слева по φ, а справа по λ, находим, что
ифференцируя (2.7) слева по φ, а справа по λ, находим, что 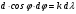 , откуда
, откуда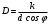 . (6)
. (6)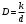 . (7)
. (7)  ольшая дисперсия оптических приборов (в том числе дифракционной решетки) является необходимым, но не достаточным условием для раздельного наблюдения двух близлежащих линий. В зависимости от крутизны кривой интенсивности соседние максимумы длин волн λ1 и λ2 могут наблюдаться как два самостоятельных или как один максимум. Как видно из рис. 5, при одинаковой угловой дисперсии линий λ1 и λ2 возможность их разрешения (раздельного восприятия) различна. Так, на рис. 5 слева минимум между линиями λ1 и λ2 , отсутствует, и эти линии не различаются как самостоятельные, а на рис. 5 справа имеются наблюдаемые минимумы между линиями λ1 и λ2.
ольшая дисперсия оптических приборов (в том числе дифракционной решетки) является необходимым, но не достаточным условием для раздельного наблюдения двух близлежащих линий. В зависимости от крутизны кривой интенсивности соседние максимумы длин волн λ1 и λ2 могут наблюдаться как два самостоятельных или как один максимум. Как видно из рис. 5, при одинаковой угловой дисперсии линий λ1 и λ2 возможность их разрешения (раздельного восприятия) различна. Так, на рис. 5 слева минимум между линиями λ1 и λ2 , отсутствует, и эти линии не различаются как самостоятельные, а на рис. 5 справа имеются наблюдаемые минимумы между линиями λ1 и λ2. 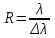 . (8)
. (8) линейно расположенных источников в точке
линейно расположенных источников в точке  на экране. Кроме того, поскольку положение точки
на экране. Кроме того, поскольку положение точки 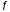 к прямой, перпендикулярной линии источников, то будем строить зависимость интенсивности непосредственно от угла
к прямой, перпендикулярной линии источников, то будем строить зависимость интенсивности непосредственно от угла 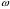 , расположенных на равных расстояниях один от другого и обладающих равными амплитудами
, расположенных на равных расстояниях один от другого и обладающих равными амплитудами 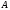 . Пусть разность фаз между осцилляторами составляет фазовый угол
. Пусть разность фаз между осцилляторами составляет фазовый угол 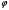 . Разность фаз создается либо из-за выбора фазовых сдвигов колебаний осцилляторов, либо потому, что мы находимся под углом к линии осцилляторов. Независимо от причин возникновения фазового сдвига нам
. Разность фаз создается либо из-за выбора фазовых сдвигов колебаний осцилляторов, либо потому, что мы находимся под углом к линии осцилляторов. Независимо от причин возникновения фазового сдвига нам 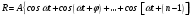 . (1)
. (1)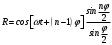 . (2)
. (2)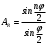 , (3)
, (3)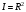 , то для амплитуды интенсивности пишем
, то для амплитуды интенсивности пишем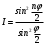 . (4)
. (4)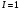 , а при двух осцилляторах
, а при двух осцилляторах 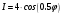 .
.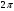 )
)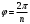 1 минимум)
1 минимум)

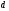 друг от друга. В нашем приближении мы пренебрегаем шириной источников осцилляторов. Как видно из рисунка 2, разность фаз волн обоих источников равна числу волн заключенных на отрезке
друг от друга. В нашем приближении мы пренебрегаем шириной источников осцилляторов. Как видно из рисунка 2, разность фаз волн обоих источников равна числу волн заключенных на отрезке 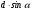 , умноженному на
, умноженному на 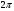 . Поэтому разность фаз двух источников равна
. Поэтому разность фаз двух источников равна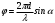 .. (5)
.. (5)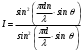 .
.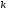 число щелей решетки. Сколько добавочных минимумов возникает между основными максимумами.
число щелей решетки. Сколько добавочных минимумов возникает между основными максимумами. 