Числа Фибоначчи. Числа Фибоначчи
 Скачать 291.56 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Факультет среднего профессионального образования Машиностроительный колледж Индивидуальный проект По дисциплине Математика По теме: «Числа Фибоначчи» Студент группы мМТО 21 – 1 Тайбинов Данил Сергеевич Проверил(а) Загоскина Е.Б Содержание Введение…………………………………………….2 Обоснование выбора……………………………….3 Цель работы…………………………………………3 Задачи работы .…………………………………….. 3 Основная часть…………………………………..4-13 Выводы …………………………………………….14 Список используемых источников ………………15 Введение «Числа управляют миром! Число – это сила, царящая над богами и смертными!» - так говорили ещё древние пифагорейцы. Актуальна ли в наши дни эта основа учения Пифагора? Что такое числа Фибоначчи, где эти числа можно увидеть, где их можно встретить в нашей повседневной жизни, почему эта последовательность чисел столь распространена в нашем мире? Такие вопросы возникли на уроке алгебры при изучении темы «Последовательности». В учебнике (Алгебра. 9 класс: Ю.Н. Макарычев, Н.Г. Миндюк и д.р.) приведён следующий пример: Пусть (un) последовательность, в которой u1=1, u2=1, un+1=un+un-1 при 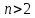 . Выпишем первые несколько её членов: 1,1,2,3,5,8,13,21,34,55, … Эта последовательность описана в работах итальянского математика Леонардо из Пизы, известного под именем Леонардо Фибоначчи (1180-1240). Члены этой последовательности называют числами Фибоначчи.Существует множество исследований, которые показывают где можно встретить последовательность Фибоначчи в самых разнообразных областях окружающей нас действительности. Мне захотелось прикоснуться к этим знаниям и провести своё исследование. Результатом моей теоретической и практической деятельности явилась данная исследовательская работа, которая частично отвечает на интересующий меня вопрос: «Где «живут» числа Фибоначчи?». Обоснованность выбора Актуальность выбранной темы заключается в том, что числа Фибоначчи и их различные инварианты отражаются во всех творениях мироздания, которые продуманы и подчинены единым законам природы и имеют большой практический и теоретический интерес во многих науках. Исследование заключается в том, что приобретаются новые знания, за рамками учебного предмета, знания, которые необходимы каждому образованному человеку, потому что числа Фибоначчи встречаются ежедневно в окружающей нас действительности. Цель исследования: изучить проявление чисел Фибоначчи и связанного с ним закона золотого сечения в строении живых и неживых объектов; найти примеры использования чисел Фибоначчи. Задачи работы: описать способ построения ряда Фибоначчи и спирали Фибоначчи. Увидеть математические закономерности, в строении человека, растительного мира и неживой природы с точки зрения феномена Золотого сечения. Основная часть Биография Леонардо Пизано Фибоначчи рис(1)Леонардо Пизанский (Фибоначчи)– это один из крупнейших Европейских средневековых математиков первой величины, труды которого включили в себя ценнейшие знания в области математики той поры. Он превзошел знаниями лучших ученых своей эпохи, опередив их практически на две сотни лет, заложив тем самым фундамент развития науки в западной Европе на основе математических знаний арабов и индусов. Более известен под прозвищем Фибоначчи, что в переводе с итальянского означает «хороший сын родился». Точная дата его рождения неизвестна. Предположительно Фибоначчи родился в 1170 г. в городе Пиза, в Италии. Будучи рождённым в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты. Его отец был купцом и государственным вельможей. Тогда Пиза была одним из крупнейших коммерческих центров, активно сотрудничавших с исламским Востоком, и отец Фибоначчи энергично торговал на северном побережье Африки, по торговым делам часто бывал в Алжире. Благодаря этому ему удалось «устроить» своего сына в одну из арабских школ, где он смог получить превосходное для того времени математическое образование. Леонардо изучал труды математиков востока, по арабским переводам он ознакомился также с достижениями античных и индийских математиков. Все эти знания он впитывал в себя как губка, а потом принес их в Европу. Он «открыл» для европейцев арабские цифры вместо римских цифр и десятичную систему счисления. Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» («Libег аЬасi», 1202; до наших дней сохранилась только дополненная рукопись 1228 г.). Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной, и одной из величайших открытий всех времён и народов – десятичную систему счисления. На протяжении нескольких столетий по труду Фибоначчи ученые знакомились с двумя важнейшими разделами математики – арифметикой и алгеброй и черпали из него задачи и оригинальные методы решения, благодаря чему уже в XV – XVI вв. те разошлись по многочисленным итальянским, французским, немецким, английским, а позже и русским рукописям, печатным книгам и учебникам. Когда Леонардо вернулся в Италию, там правил император Фридрих II. Он не признавал рыцарские турниры, вместо них он проводил гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами. На таких турнирах и заблистал талант Леонардо Фибоначчи. Предположительно Фибоначчи умер во время одного из Крестовых походов в 1228 году, сопровождая императора Фридриха II. История ряда Фибоначчи Считается, что Леонардо Фибоначчи совершил открытие чисел (впоследствии названных его именем) случайно. В 1202 году он пытался решить практическую задачу: какой максимальный приплод может дать одна пара кроликов за год и создать формулу, описывающую последовательность их размножения. Задача: на второй месяц мы будем иметь одну пару, на третий месяц 1+1=2, на четвертый месяц 2+1=3 пары, на пятый месяц 3+2=5 пар, на шестой месяц 5+3=8 пар. Разгадкой стал числовой ряд, каждое последующее число которого, является суммой двух предыдущих. Отслеживая каждый месяц, количество пар кроликов получили такой ряд чисел: 1,1,2,3,5,8,13,21,34,55,89,144,233,377… Числа, образующие данную последовательность называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи. когда появился ряд Фибоначчи, никто, в том числе и он сам, не подозревал, насколько близко ему удалось приблизиться к разгадке одной из величайших тайн мироздания! Учёные, анализируя дальнейшее применение этого числового ряда к природным феноменам и процессам, обнаружили, что эти числа содержатся буквально во всех объектах живой природы, в растениях, в животных и в человеке. Фибоначчи вёл отшельнический образ жизни, много времени проводил на природе, и, гуляя в лесу, он обратил внимание, что эти числа стали буквально преследовать его. Повсюду в природе он снова и снова встречал эти числа. Например, лепестки и листья растений строго укладывались в данный числовой ряд. У многих цветов количество лепесточков – именно числа из ряда Фибоначчи. Например: ирис, 3леп. лютик, 5 леп златоцвет, 8 леп . дельфиниум, 13 леп . маргаритки,55леп. цикорий,21леп. астра, 34 леп . В числах Фибоначчи существует интересная особенность: частное от деления последующего числа Фибоначчи на предыдущее, по мере роста самих чисел, стремиться к 1,618. Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне именуется как золотое сечение или золотая пропорция. В алгебpе это число обозначается гpеческой буквой φ(фи). Итак, φ = 1,618. 233 / 144 = 1,618 377 / 233 = 1,618 610 / 377 = 1,618 987 / 610 = 1,618 1597 / 987 = 1,618 2584 / 1597 = 1,618 Сколько бы раз мы не делили одно на другое, соседнее с ним число, мы всегда получим 1, 618. А если сделаем наоборот, то есть разделим меньшее число на большее, то получим 0, 618, это число, обратное к 1, 618, тоже называется золотой пропорцией. Для практических целей ограничиваются приблизительным значением 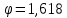 = 1,618. В процентном округлённом значении з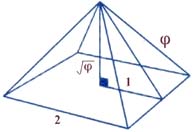олотое сечение — это деление какой-либо величины в отношении 62 % и 38 %. Число называется также золотым числом. З  олотое сечениеПринято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.  Рис(3) Рис (2) Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал пятиугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Это название до сих пор является самым популярным. Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства. 4) Золотой прямоугольник и спираль Фибоначчи Золотой прямоугольник с длинной стороной a и короткой b, помещённый рядом с квадратом со стороной a, даёт подобный золотой прямоугольник с длинной стороной a + b и короткой стороной a. Это иллюстрирует отношение 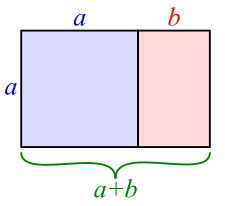  Рис (4)Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. 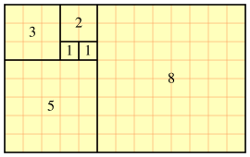 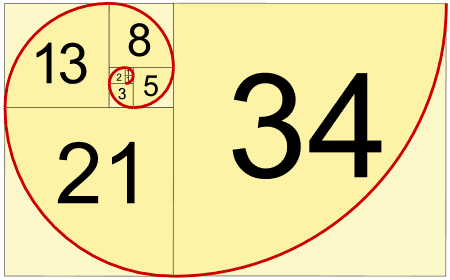 Рис (5) Рис (6) Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (спираль Фибоначчи). Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. План города Ауро-вилля (Индия)—свидетельство спиралевидной застройки. Молекула ДНК закручена двойной спиралью. Гёте называл спираль «кривой жизни». Встретить числовые закономерности в живой природе можно в различных спиральных формах, которыми так богат мир растений. Обычно можно усмотреть два вида спиралей. В одном спирали завиваются по часовой стрелке, а в другом против. Число "правых "и "левых" спиралей часто оказываются соседними числами Фибоначчи. Можно привести множество примеров. Семена в подсолнухе распределяются по спирали. Они растут по и против часовой стрелки от центра цветка. Количество этих спиралей – это два числа, идущих подряд в последовательности Фибоначчи 21 и 34 или 34 и 55. Особенно много спиралей можно наблюдать в расположении семечек крупного подсолнуха. Их число в каждом из направлений может достигать 55 и 89. Посмотрим на сосновую шишку. Чешуйки на ее поверхности расположены строго закономерно — по двум спиралям, которые пересекаются приблизительно под прямым углом. Число таких спиралей у сосновых шишек равно 8 и 13 или 13 и 21. Числа Фибоначчи и природа Великий астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Среди придорожных трав растет ничем не примечательное растение —цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий — 38, четвертый — 24 и т. д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения. 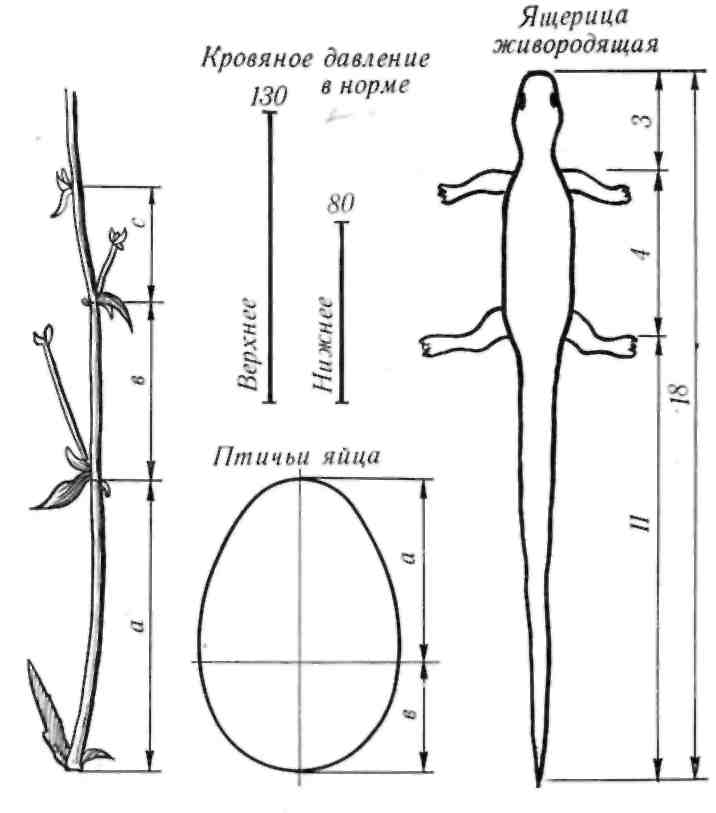 В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции: длина ее хвоста так относится к длине остального тела, как 62 к 38.И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы — симметрия относительно направления роста и движения. Здесь золотое сечение в пропорциях частей перпендикулярно к направлению роста. Сон и бодрствование человека в пределах суток, удары сердца и его отдых, кровяное давление в норме — все имеет тенденцию проявляться в золотой пропорции. Рис (7) Числа Фибоначчи и человекОколо двух веков идея применения золотой пропорции в исследовании человеческого тела была предана забвению, и лишь в середине XIX века немецкий ученый Цейзинг вновь обратился к ней. Он находил, что все тело человека в целом и каждый отдельный его член связаны математически строгой системой пропорциональных отношений, среди которых золотое сечение занимает важнейшее место. Измерив тысячи человеческих тел, он установил, что золотая пропорция есть среднестатистическая величина, характерная для всех хорошо развитых тел. Он нашел, что средняя пропорция мужского тела близка к 13/8=1,625, а женского — к 8/5=1,60. Кроме этого есть и еще несколько основных золотых пропорции нашего тела: 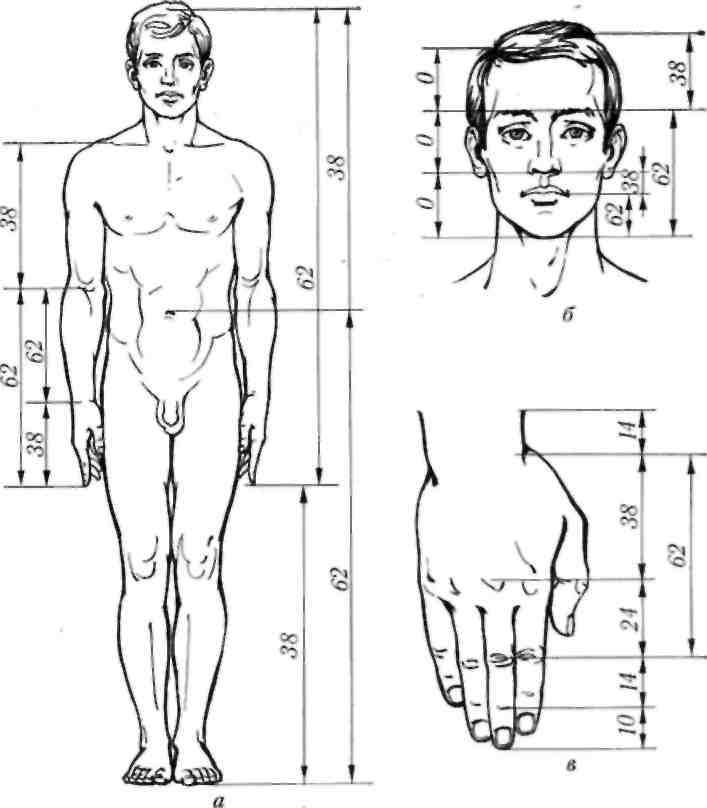 - расстояние от кончиков пальцев до запястья и от запястья до локтя равно 1:1,618 - расстояние от уровня плеча до макушки головы и размера головы равно 1:1,618 - расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1,618 - расстояние точки пупа до коленей и от коленей до ступней равно 1:1,618 - расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1,618 - расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1,618 - расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1,618 В строении черт лица человека есть множество примеров, приближающихся по значению к формуле золотого сечения. Однако не бросайтесь тотчас же за линейкой, чтобы обмерять лица всех людей. Потому что точные соответствия золотому сечению, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно, точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора. Д 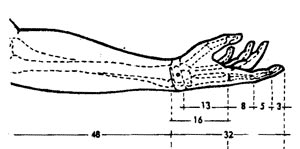 остаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг. У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух фаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи. Измерение инструментов, которыми человек пользуется почти ежедневно, показало, что в них он продолжает формообразование по закону золотой пропорции, проявленное природой в строении руки и кисти. 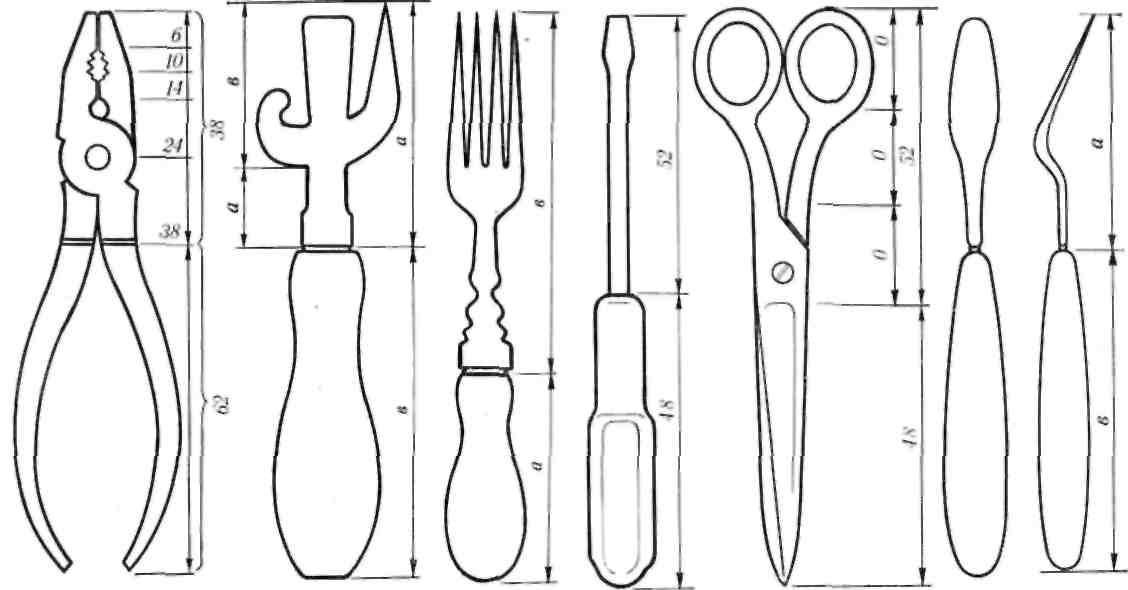 Рис (8) Числа Фибоначчи и искусствоЗолотое сечение было использовано, чтобы привнести красоту, баланс и гармонию в некоторые величайшие произведения искусства. Литература Например, проведенный Н. А. Васютинским (автор книги «Золотая пропорция»), анализ стихотворений А. С. Пушкина с этой точки зрения показал, что размеры стихов распределены весьма неравномерно; оказалось, что Пушкин явно предпочитает размеры в 5, 8, 13, 21 и 34 строк (числа Фибоначчи). Представляет несомненный интерес анализ романа «Евгений Онегин», сделанный Н. А. Васютинским. Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее отточенной и эмоционально насыщенной является восьмая глава. В ней 51 стих. Вместе с письмом Евгения Онегина к Татьяне (60 строк) это точно соответствует числу Фибоначчи 55! Ритм «онегинской» строфы несет глубокую смысловую нагрузку. Четыре формообразующих элемента строфы - это, как правило, и четыре содержательных элемента: тема, развитие, кульминация, афористическая концовка. «Онегинская» строфа была настолько оригинальным и индивидуальным изобретением Пушкина, что после Пушкина почти никто из поэтов не рисковал прикасаться к его детищу. Кульминацией главы является объяснение Евгения в любви к Татьяне -строка «Бледнеть и гаснуть ... вот блаженство!» Эта строка делит восьмую главу на две части - в первой 477 строк, а во второй - 295 строк. Их отношение равно 1, 617! Тончайшее соответствие величине золотой пропорции! Архитектура  Трудно найти человека, который бы не знал и не видел здание собора Василия Блаженного на Красной площади. Храм этот особенный; он отличается удивительным разнообразием форм и деталей, красочных покрытий; ему нет равных в нашей стране. Архитектурное убранство всего собора продиктовано определенной логикой и последовательностью развития форм. Исследуя его, пришли к выводу о преобладании в нем ряда золотого сечения. Если принять высоту собора за единицу, то основные пропорции, определяющие членение целого на части, образуют ряд золотого сечения: 1: j: j 2: j 3: j 4: j 5: j 6: j 7, где j =0,618. В этом членении и заключена основная архитектурная идея создания собора, единая для всех восьми куполов, объединяющая их в одну композицию. Золотое сечение в скульптуре и живописи Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния.  Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения. Пропорции золотого сечения создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения”. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. Рис(9) А 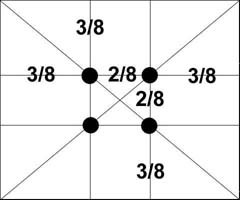 художники еще в эпоху Возрождения открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, они делят величину изображения по горизонтали и вертикали в золотом сечении, т.е. расположены они на расстоянии примерно 3/8 и 5/8 от соответствующих краев плоскости. Рис(10)Практическое исследование Теперь применим полученные знания на практике. Проведем измерения среди учащихся 9 класса.
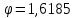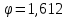В эксперименте приняли участие 6 учащихся 9 класса, 4 девочки и 2 мальчика. Измерялся рост и расстояние от талии до пола. Результаты отражены в таблицы. Одна учащаяся идеального телосложения, для неё отношение роста к расстоянию от пупка до пола равно  1. Ещё одна учащаяся очень близка к золотому сечению: . В результате проведенных измерений 33% участников имеют идеальные параметры. Эти результаты в процентах тоже близки к золотому сечению 68% и 32%.Задача «Имеется 76 карточек, на которых написаны разные числа. Эти карточки разложены на столе по кругу числом вниз. Надо найти какие-нибудь три идущие подряд карточки такие, что число, написанное на средней из этих трёх карточек, больше, чем на двух соседних. Перевернут можно последовательно не более 10 карточек. Как надо действовать, чтобы наверняка найти три карточки, для которых выполняется указанное условие?» Решение: Для построения рассуждений нам потребуется последовательность Фибоначчи: 1; 1; 2; 3; 5; 8; 13; 21; … an = an—1 + an – 2 , а1 = а2 = 1. Число карточек 76 = 21 + 21 + 34. (т. е. можно будет использовать данную закономерность) Пусть N карточек расположены по кругу в вершинах N – угольника. Если a, b – карточки, то (a; b) – «a лежит раньше b по часовой стрелке». Дуга (a; b) – промежуток между a и b. Длина дуги (a; b) – число сторон N – угольника между a и b. Назовём тройкой ранга k три открытые (числом вверх) карточки (a; b; c), удовлетворяющие условиям: на дугах (a; b) и (b; с) нет открытых карточек; длины дуг (a; b) и (b; с) либо обе равны xk, либо одна - xk, а вторая – xk+1; число на карточке b больше числа на карточке а и с. В нашей задаче надо найти тройку ранга 1. Посмотрим, как из тройки ранга k получить тройку ранга 1. Пусть тройка (a; b; c) – тройка ранга k . 1 случай: длина обеих дуг (a; b) и (b; с) равны xk. На дуге (a; b) откроем точку d так, что длины дуг (a; d) и (d; b) равны xk-2 и xk-1 соответственно. При этом возможны два варианта: а) d < b ⟹ (d; b; c) – тройка ранга k – 1; б) d > b ⟹ (a; d; b) – тройка ранга k – 2. 2 случай: Длина дуги (a; b) - xk+1 (для определённости), а дуги (b; с) - xk. На большей дуге откроем точку d так, что длины дуг (a; d) и (d; b) равны xk xk-1. Возможны два варианта: а) d < b ⟹ (d; b; c) – тройка ранга k – 1; б) d > b ⟹ (a; d; b) – тройка ранга k – 1. Применяя последовательно (в обоих случаях) этот способ мы получим тройку ранга 1, открыв при этом не более k – 1 карточки. Остаётся для решения найти какую-нибудь тройку ранга k. В нашем случае: N = 76 = 21 + 21 + 34 = 2 xk + xk+1. И всего (с начальными a; b и с нам предстоит открыть k + 2 числа, т. е. в нашем случае – 10 чисел). Ответ: Для нахождения данной тройки чисел достаточно открыть 10 карточек. Выводы Работая над проектом, я убедился в том, что красота таинственна, разнообразна и окружает нас повсюду, но вся она поддается одним и тем же законам, знание и применение которых делает нашу жизнь прекраснее. Сосновые шишки, раковины улиток, волны океана, рога животных, облака циклона и галактики – все они образуют логарифмические спирали. Даже человеческий палец, который составлен из трех фаланг, находящихся по отношению друг к другу в Золотой пропорции, принимает спиральную форму, когда сжимается. Вечность времени и световые годы космоса разделяют сосновую шишку и спиральную галактику, но строение остаётся тем же самым: коэффициент 1,618! Оказалось, что пропорция 1, 618, которую дают числа Фибоначчи, постоянно встречается в форме самых различных предметов вокруг нас, как природного, так и искусственно происхождения. Причем в ряде случаев такая пропорция соблюдается человеком сознательно, а зачастую – совершенно бессознательно. Для наглядности часто приводят такой интересный факт: если человек садится на пустую скамейку, чаще всего он сядет не посередине, а ближе к одному ее краю, разделив собой скамейку в полном соответствии с пропорцией золотого сечения. Возможно, это первостепенный закон, управляющий природными явлениями. Таким образом, гипотеза о существовании особых числовых закономерностей, которые отвечают за гармонию, подтверждается. Действительно, всё в мире продуманно и просчитано самым главным нашим дизайнером – Природой! У природы есть свои законы, выраженные с помощью математики, и математика – это очень важный инструмент для познания её тайн. Список используемых источников Числа Фибоначчи — Википедия (wikipedia.org) Фибоначчи — Википедия (wikipedia.org) Ресурсы удаленного доступа [электронный ресурс; рисунки] - Режим доступа: http://festival.1september.ru Режим доступа: https://ru.wikipedia.org/wiki/Золотое_сечение Иркутск 2022 |
