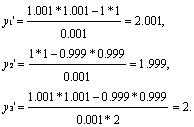Практическое занятие № 3. Численное дифференцирование

• Название: Численное дифференцирование
• Дата: 16.03.2023
• Размер: 36.87 Kb.
• Имя файла: Практическое занятие № 3.docx
• Тип: Занятие; #994155

Практическое занятие №3

Тема: Численное дифференцирование

Цель работы: изучение численного дифференцирования и метода Эйлера.
Теоретическое обоснование:
Производная функции есть предел отношения приращения функции к приращению независимой переменной при стремлении к нулю приращения независимой переменной

.

При численном нахождении производной заменим отношение бесконечно малых приращений функций и аргумента   отношением конечных разностей. Очевидно, что чем меньше будет приращение аргумента, тем точнее численное значение производной.

Первая производная. Двухточечные методы.

Для двухточечных методов при вычислении производных используется значение функции в двух точках. Приращение аргумента задается тремя способами, откладывая Δx = h вправо, влево и в обе стороны от исследуемой точки. Соответственно получается три двухточечных метода численного дифференцирования:

метод 1
метод 2
метод 3

Суть указанных методов проиллюстрирована на рисунке. Численное значение тангенса угла α образованного касательной к графику y(x) и осью абсцисс, показывает точное значение производной(геометрический смысл производной). Тангенсы углов α₁, α₂, α₃ соответствуют приближенным значениям производных, определенных методами 1,2,3 соответственно (подумайте почему?).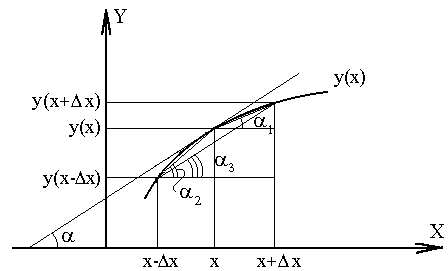



Пример. Вычислить точное и приближенное (тремя методами) значения производной функции y=x*x в точке x=1 с шагом h=1 и h=0.001.

Этапы решения задачи приведены в таблице.

Таблица

N	Этап программирования	Выполнение
1.	Постановка задачи	Вычислить точное и приближенное (тремя методами) значения производной функции y=x*x в точке x=1 с шагом h=1 и h=0.001.
2.	Математическое описание	Аналитическое решение: y'=2x , y'(1)=2, Численное решение для шага: h=1 , для шага h=0.001
3.	Разработка структограммы	Выполнить самостоятельно
4.	Написание программы	Выполнить самостоятельно
5.	Отладка и получени результатов	Выполнить самостоятельно

Вычисление первых производных по трёхточечным схемам.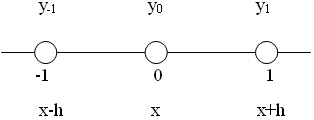



Расчетные формулы для указанной трехточечной схемы имеют вид:



Вычисление производных второго порядка.

Вторая производная вычисляется как первая производная от первой производной. Для следующей пятиточечной схемы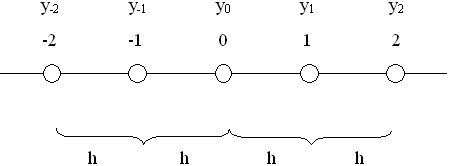



расчетная формула имеет вид:


Ход работы:

1. 
   Напишите 3 примера решения задач при помощи численного дифференцирования
   
2. 
   Методы численного дифференцирования функций. Напишите 4 метода
   

3. Оптимизация шага численного дифференцирования при ограниченной точности задания значений функции. Опишите 2 примера решения задач
Контрольные вопросы:

1. 
   Что такое производная функция?
   
2. 
   Что такое численное дифференцирования?
   
3. 
   Что такое оптимизация шага
   

Содержание отчёта
1.Номер, тема и цель работы.

2.Письменный ответ на контрольные вопросы.

3. Практическая работа выполняется на одной стороне листа писчей бумаги формата А4 по форме 5 – первый лист и 5а – последующие. Пишется от руки чётко, аккуратно, полными словами, без сокращений, за исключением тех, что установлены ГОСТом 2.316-68, 3.1702-79 или печатается на компьютере шрифтами Times New Roman.
Литература

1. 
   Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Наука, 1987. – 432 с.
   
2. 
   Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989. – 432 с.
   
3. 
   Вержбицкий В.М. Основы численного анализа. − М.: Высшая школа, 2001. − 840 с
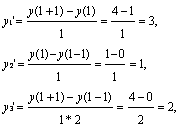