Отчет. Отчет 7. Численное интегрирование
 Скачать 304.09 Kb. Скачать 304.09 Kb.
|
|
«Численное интегрирование» ContentsПостановка задачи 3 Метод прямоугольников 4 Метод трапеций 6 Метод Симпсона 7 Результат 8 Постановка задачиТребуется вычислить определенный интеграл 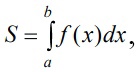 где 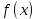 — подынтегральная функция, — подынтегральная функция, 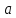 и и 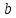 — нижний и верхний пределы интегрирования. — нижний и верхний пределы интегрирования.Численное интегрирование — это вычисление определенного интеграла путем замены подынтегральной функции более простой аппроксимирующей функцией, последующего прямого интегрирования и получения расчетных формул. К формулам численного интегрирования обращаются, когда невозможно найти первообразную или она очень сложна для вычислений. Функция: 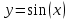 Задание: 1. Для заданной функции 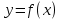 из числа элементарных найти точное значение определенного интеграла на выбранном отрезке. из числа элементарных найти точное значение определенного интеграла на выбранном отрезке.Вычислить интеграл приближенно по формулам: прямоугольников (левых, правых, средних); по формуле трапеций; по формуле Симпсона. Вывести точное значение, приближенное значение, практическую погрешность 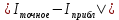 , теоретическую оценку погрешности. , теоретическую оценку погрешности.2. Рассчитать, сколько достаточно взять число интервалов 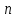 , чтобы найти значение интеграла , чтобы найти значение интеграла 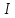 с точностью с точностью 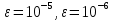 . .Вывести точное значение, приближенное значение, практическую погрешность 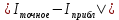 , необходимое число узлов , необходимое число узлов 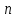 . .Метод прямоугольниковПодынтегральная функция 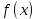 заменяется кусочно-постоянной функцией, т.е. функцией, постоянной на каждом отрезке заменяется кусочно-постоянной функцией, т.е. функцией, постоянной на каждом отрезке 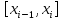 . Значения этой постоянной на каждом отрезке будет разным, равным . Значения этой постоянной на каждом отрезке будет разным, равным 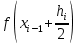 . .Искомая площадь заменяется суммой площадей соответствующих прямоугольников. На каждом элементарном отрезке 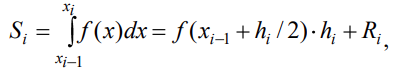 а на всем отрезке 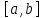 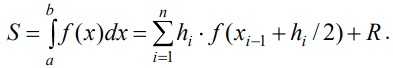 Общая формула прямоугольников имеет вид: 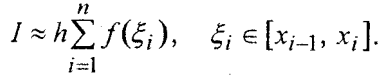 Если пренебречь погрешностью 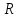 на всем отрезке, то последнее уравнение даст составную квадратурную формулу для метода прямоугольников (средних). на всем отрезке, то последнее уравнение даст составную квадратурную формулу для метода прямоугольников (средних).При фиксировании точки 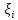 на элементарных отрезках на элементарных отрезках 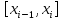 получаем формулы левых и правых прямоугольников соответственно: получаем формулы левых и правых прямоугольников соответственно: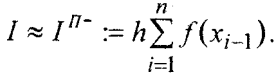 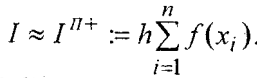 Формулы для вычисления теоретической погрешности 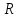 для средних, левых и правых прямоугольников соответственно: для средних, левых и правых прямоугольников соответственно: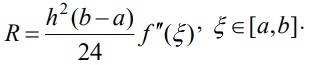 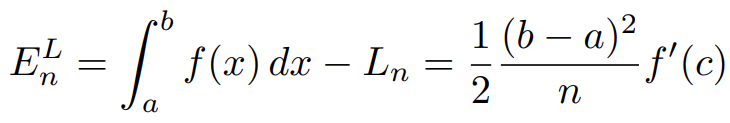 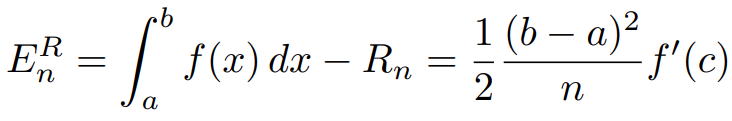 Метод трапецийМетод трапеций использует для описания функции 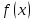 линейную интерполяцию, заменяя ее кусочно-линейной функцией на отрезке линейную интерполяцию, заменяя ее кусочно-линейной функцией на отрезке 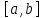 , т. е. ломаной, соединяющей точки , т. е. ломаной, соединяющей точки 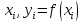 . .В этом случае искомая площадь заменяется суммой трапеций. Площадь этой трапеции легко вычисляется и дает квадратурную формулу 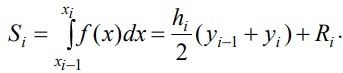 Составная формула: 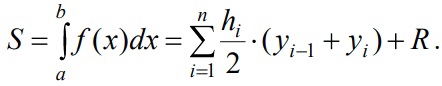 Формула вычисления теоретической погрешности на всем интервале: 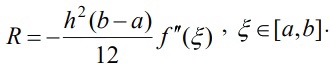 Метод СимпсонаПовышение точности численного интегрирования в методе Симпсона достигается за счет повышения точности интерполяции — функция 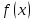 заменяется интерполяционным многочленом Лагранжа второй степени (квадратичная интерполяция). заменяется интерполяционным многочленом Лагранжа второй степени (квадратичная интерполяция).Разобьем отрезок интегрирования 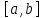 на четное число равных частей, полагая, что шаг между заданными точками на четное число равных частей, полагая, что шаг между заданными точками 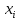 равен равен 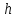 . Рассмотрим два соседних интервала . Рассмотрим два соседних интервала 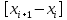 и и 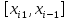 . .Проведем через три точки 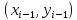 , , 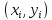 , , 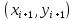 интерполяционный многочлен Лагранжа второй степени интерполяционный многочлен Лагранжа второй степени 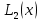 . Вычислим определенный интеграл на отрезке . Вычислим определенный интеграл на отрезке 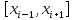 , заменив подынтегральную функцию , заменив подынтегральную функцию 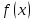 многочленом многочленом 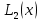 . После интегрирования получим квадратурную формулу метода Симпсона на отрезке . После интегрирования получим квадратурную формулу метода Симпсона на отрезке 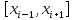 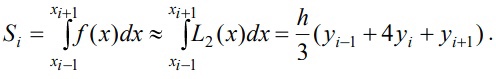 Составная формула: 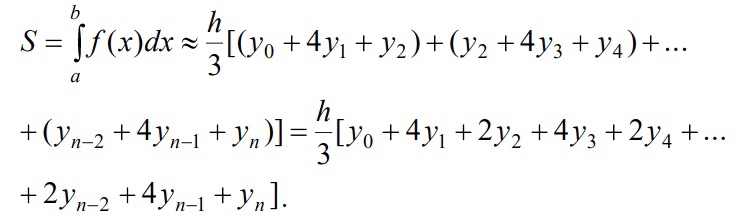 Формула теоретической погрешности на всем отрезке: 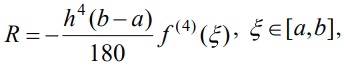 где 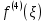 — четвертая производная исходной функции в некоторой точке — четвертая производная исходной функции в некоторой точке 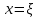 . .РезультатВычисление определенного интеграла на отрезке 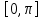 . С количеством интервалов 6. . С количеством интервалов 6.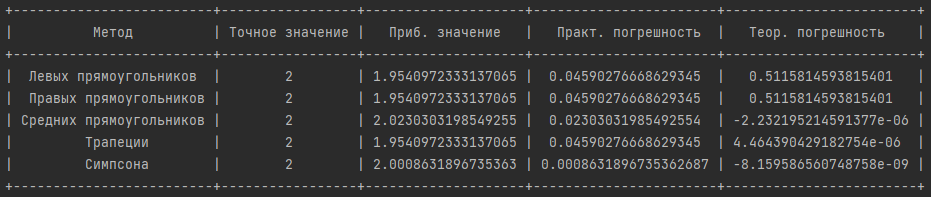 Подбор значений количества интервалов при точностях ε=10^-3 и ε=10^-5. 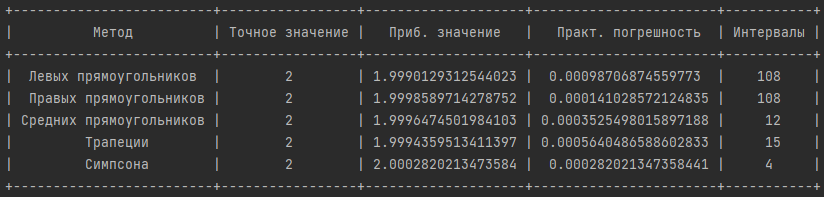 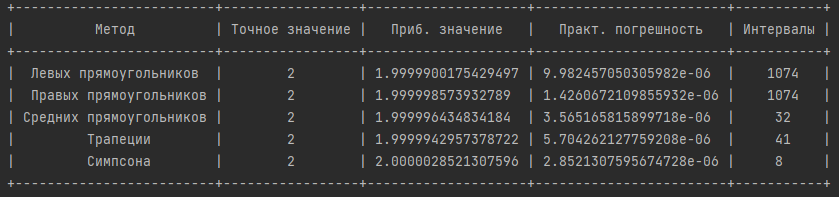 |
