[МОР] Лабораторная №3. Численное интегрирование
 Скачать 168.84 Kb. Скачать 168.84 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ Кафедра компьютерных систем в управлении и проектировании (КСУП) Отчёт к лабораторной работе №3 по дисциплине «Методы оптимальных решений» по теме «Численное интегрирование» Выполнил: Студент группы 586-1 _____Мазуренко А. А. «__»_______ 2019 г. Принял: Преподаватель кафедры КСУП ______Кибиткин В.В. «__»________2019 г. Томск 2019 Содержание1 ВведениеЗадание на лабораторную работу: Для функции, выполнить численное нахождение определенного интеграла в указанных пределах. Реализовать метод центральных прямоугольников, метод трапеций и метод Симпсона, заполнив таблицу. Найти приближенное значение интеграла и точное; оценить абсолютную и относительную погрешность расчета. Сравнить полученные результаты друг с другом и результатом аналитического расчета значения интеграла; дать анализ. Оценить абсолютную и относительную погрешность расчета методом Симпсона. Вариант №4 Функция:  Интервал интегрирования: 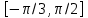 2 Теоретическая информацияМетод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. 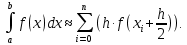 Ниже на рисунке 2.1 проинтегрирована функция 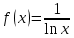 методом центральных (средних) прямоугольников. методом центральных (средних) прямоугольников.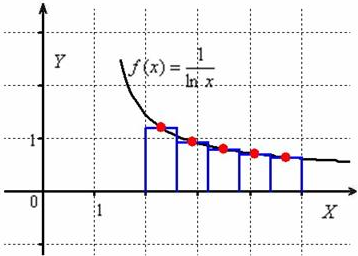 Рисунок 2.1 – Интегрирования методом центральных (средних) прямоугольников функции 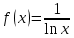 Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. 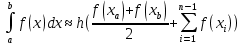 Ниже на рисунке 2.2 проинтегрирована функция 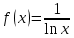 методом трапеции. методом трапеции.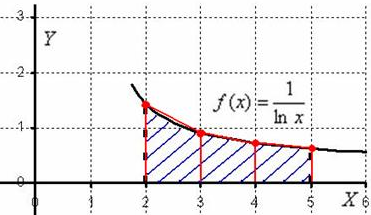 Рисунок 2.2 – Интегрирования методом трапеции функции 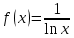 Формула Симпсона относится к приёмам численного интегрирования. Суть метода заключается в приближении подынтегральной функции на отрезке  Ниже на рисунке 2.3 расположен график для аналитического расчета методом Симпсона. 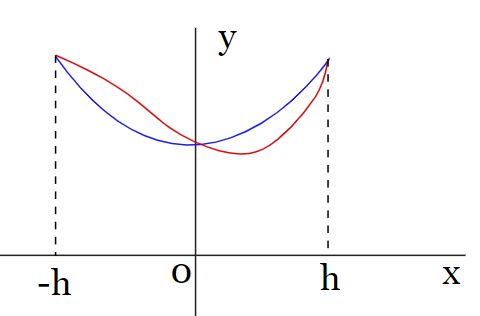 Рисунок 2.3 – График аналитического расчета методом Симпсона Получаем систему уравнений для нахождения коэффициентов параболы: 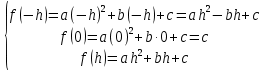 Перейдем к нахождению интеграла:  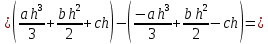 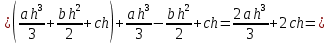 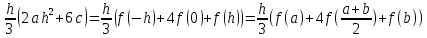 Таким образом, можно получить формулу метода парабол: 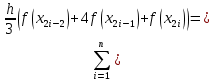  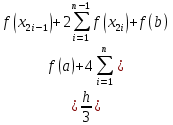 Абсолютная погрешность для формул трапеций и парабол оцениваются такими формулами: 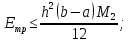 (2.1) (2.1) (2.2) (2.2)где 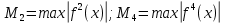 Допустим, что интеграл  вычислен по формуле Симпсона дважды при различных значениях h. Пусть 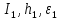 соответственно обозначают найденный результат, значение шага h и погрешность первого вычисления, а соответственно обозначают найденный результат, значение шага h и погрешность первого вычисления, а 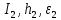 – те же величины при втором вычислении. – те же величины при втором вычислении.Тогда согласно формулам 2.2 имеем 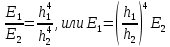 (2.3) (2.3)В частности, если  , получаем , получаем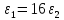 И для точного значения интеграла при двух вычислениях с шагом 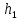 и и  имеем имеем 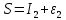 Отняв верхнее уравнение от нижнего, находим 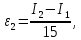 или, применяя более общие обозначения, 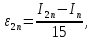 3 Результат расчетовВ результате работы программы были найдены значения интегрирования функции 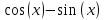 в интервале в интервале 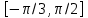 , рассчитанных с помощью метода центральных прямоугольников, метода трапеций и метода Симпсона. Выполнен расчет для различных значений шага h. Результаты работы предоставлены в таблице 3.1 , рассчитанных с помощью метода центральных прямоугольников, метода трапеций и метода Симпсона. Выполнен расчет для различных значений шага h. Результаты работы предоставлены в таблице 3.1Таблица 3.1 — Значения интегрирования
Каждый метод интегрирования при уменьшении шага h показывает все меньше и меньше погрешность интегрирования. Наилучшим методом интегрирования является метод Симпсона. Результат абсолютной погрешности при помощи формулы Симпсона для шага h = 0.1, h = 0.01 и h = 0.001: 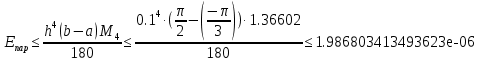 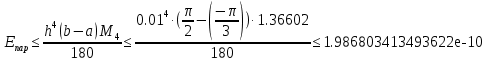  Результат относительной погрешности для шага h = 0.1, h = 0.01 и h = 0.001:  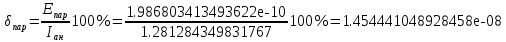 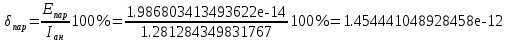 Результат оценки погрешности:  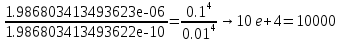   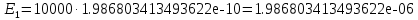 Если  , получаем , получаем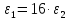  ЗаключениеВ результате выполнения данной лабораторной работы были изучены методы численного интегрирования. Метод Симпсона оказался точнее других методов численного интегрирования (метод центральных прямоугольников, метод трапеций) при разных значениях шага h. Погрешность интегрирования уменьшается при уменьшении величины шага интегрирования h. В конечном счете была изучена тема «Численное интегрирование» дисциплины «Методы оптимальных решений». Приложение АЛистинг программы clear; clc; fun=inline('cos(x)-sin(x)'); disp('Численное интегрирование '); disp('------------------------'); disp('Аналитический расчет'); [I, count] = quad('cos(x)-sin(x)', -pi/3, pi/2); disp(I); disp('------------------------'); disp('Численный расчет'); disp('При h=0.1'); my_integral=integral(fun,0.1,I); disp('При h=0.01'); my_integral=integral(fun,0.01,I); disp('При h=0.001'); my_integral=integral(fun,0.001,I); maxValue = 1.366025403784439; my_const=((pi/2)-(-pi/3)); e_absolute = ((0.1^4)*my_const*maxValue)/180 res_relative = (e_absolute/I)*100 e_absolute = ((0.01^4)*my_const*maxValue)/180 res_relative = (e_absolute/I)*100 e_absolute = ((0.001^4)*my_const*maxValue)/180 res_relative = (e_absolute/I)*100 function I = integral(fun,h,I2) x=(-pi/3):h:pi/2; disp('Метод центральных прямоугольников'); y = fun(x); I = sum(h*fun(x+(h/2))) absolute = I - I2 relative = (absolute/I2)*100 disp('Метод трапеций '); I= trapz(x,y) absolute = I - I2 relative = (absolute/I2)*100 disp('Метод Симпсона'); I=quad('cos(x)-sin(x)', -pi/3, pi/2,h) absolute = I - I2 relative = (absolute/I2)*100 end |
