Связанные задачи гидро- и аэроупругости. Численное моделирование ламинарного потока в канале. Отчёт по лабораторной 1.1. Численное моделирование ламинарного потока в канале
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
|
Санкт-Петербургский политехнический университет Петра Великого Институт машиностроения, материалов и транспорта Высшая школа машиностроения Отчёт Дисциплина: «Связанные задачи гидро и аэроупругости» Тема: «Численное моделирование ламинарного потока в канале» Студенты гр. 3331501/70601 Осман А. А. Преподаватель Гатаулин Я. А. « »________2022г. Санкт-Петербург 2022 ОглавлениеЦель работы 3 Задача 3 Исходные данные 3 Рассчитываемые параметры 3 Математическая модель 4 Создание геометрии 4 Создание сетки 5 Расчёт в Fluent 6 Анализ результатов решения 7 Векторное поле скоростей. 7 Профили скорости 9 Графики скоростей, давления и касательных напряжений 11 Сравнение аналитического решения с полученным в программе ANSYS Fluent 14 Вывод 18 Список литературы 18 Цель работыПровести численный расчет во Fluent стационарного ламинарного течения вязкой несжимаемой жидкости в трубки кольцеобразного сечения для разных значений числа Рейнольдса: 100, 200, 400. Задача1) Построить геометрию и расчетную сетку; 2) Выполнить расчет потока для заданных чисел Рейнольдса; 3) Сравнить рассчитанный коэффициент сопротивления с теоретическими значениями. Исходные данныеП  араметры геометрии трубы: араметры геометрии трубы:Поперечное сечение: кольцо; Внешний диаметр 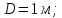 Внутренний диаметр 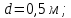  Рисунок 1 – сечение трубы Длина канала: 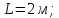 Параметры жидкости: Плотность 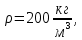 Коэффициент динамической вязкости 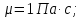 Числа Рейнольдса: 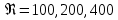 . .Граничные условия: Скорость на входе: 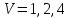 м/с; м/с;Давление на выходе: 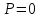 ; ;Условие прилипания на стенках: 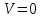 ; ;Рассчитываемые параметрыВ рассматриваемой задаче течение определяется числом Рейнольдса, определяемым по формуле: 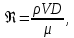 где 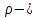 плотность жидкости, плотность жидкости, 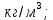 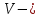 скорость потока, м/с; скорость потока, м/с; 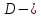 диаметр трубы, м; диаметр трубы, м;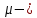 коэффициент динамической вязкости жидкости, коэффициент динамической вязкости жидкости, 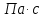 . .Параметры течения, соответствующие заданным числам Рейнольдса представлены в таблице 1. Таблица 1 – Параметры потока
Математическая модельВ качестве математической модели выбрана модель несжимаемой жидкости, течение – ламинарное, задача – стационарная. Уравнение несжимаемости: 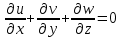 Уравнения Навье-Стокса: 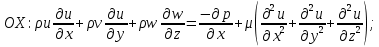 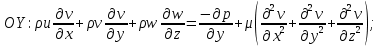 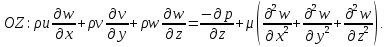 Создание геометрииДля создания геометрии трубы использовалась программа DesignModeler. Геометрия была получена с получена с помощью эскиза и операции вытягивания. 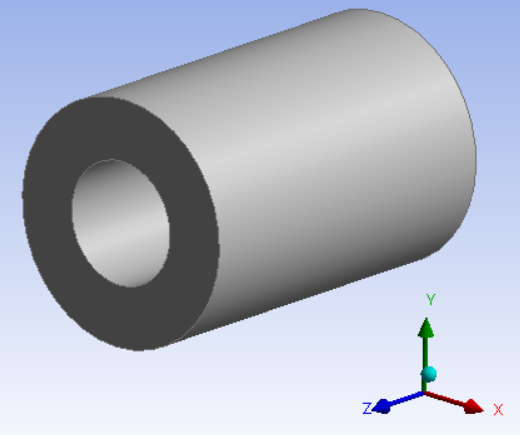 Рисунок 2 – геометрия трубы для расчёта Создание сеткиРасчётная сетка создана в программе ANSYS Meshing. Для построения сетки использован метод протяжки (Sweep), на торце задано разбиение линий, как показано на рисунке 3 (а), также использовалась опция Inflation для создания сгущения сетки к стенкам трубы (рисунок 3 (б)).   а) б) 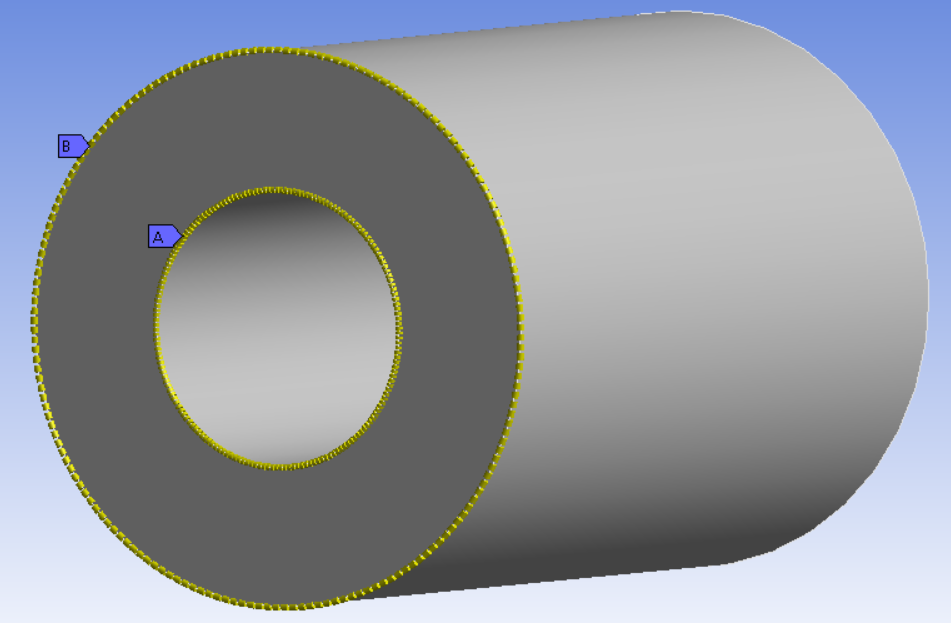  Рисунок 3 (а, б) По длине трубы в направлении оси Z задано количество разбиений и сгущение сетки к началу трубы (рисунок 4).  Рисунок 4 Количество элементов в расчётной сетке составило 440440 шт. Входу в канал, выходу и стенкам даны названия. Расчёт в FluentВ программе Fluent настроена точность, заданы параметры течения, материала, а также граничные условия.  Рисунок 5 – граничные условия. Проведён расчёт для 100 итераций, сходимость решения для Re = 400 представлена на рисунке 6. 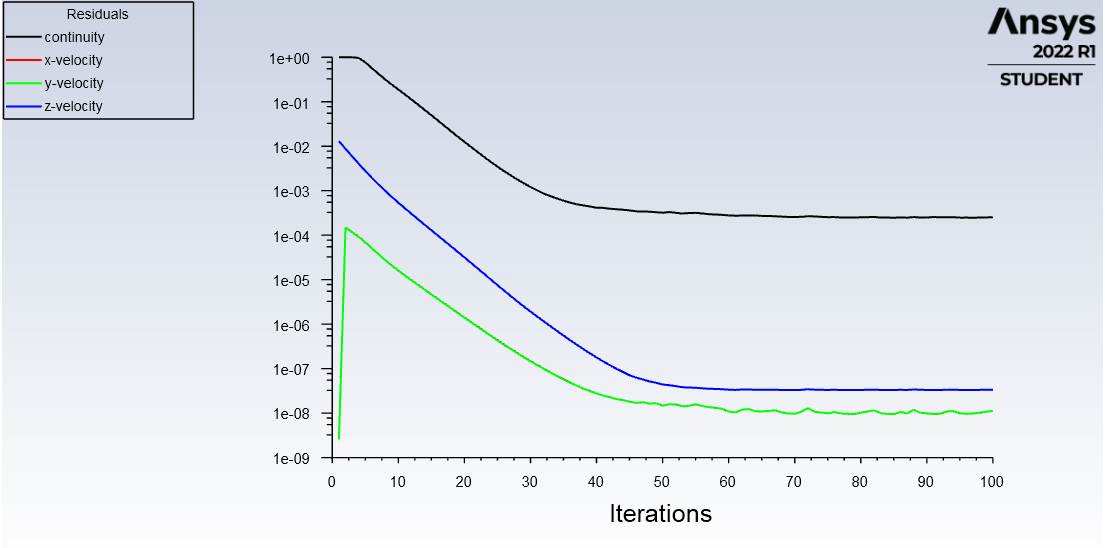 Рисунок 6 – сходимость решения. Анализ результатов решенияВекторное поле скоростей.На рисунках ниже представлены векторные поля скоростей исследуемых потоков в центральном сечении (Х=0). 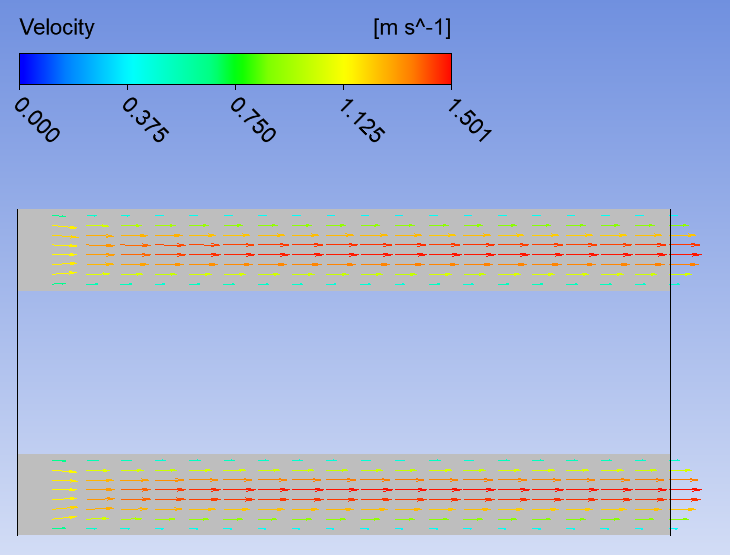 Рисунок 7 - векторное поле скоростей для Re = 100 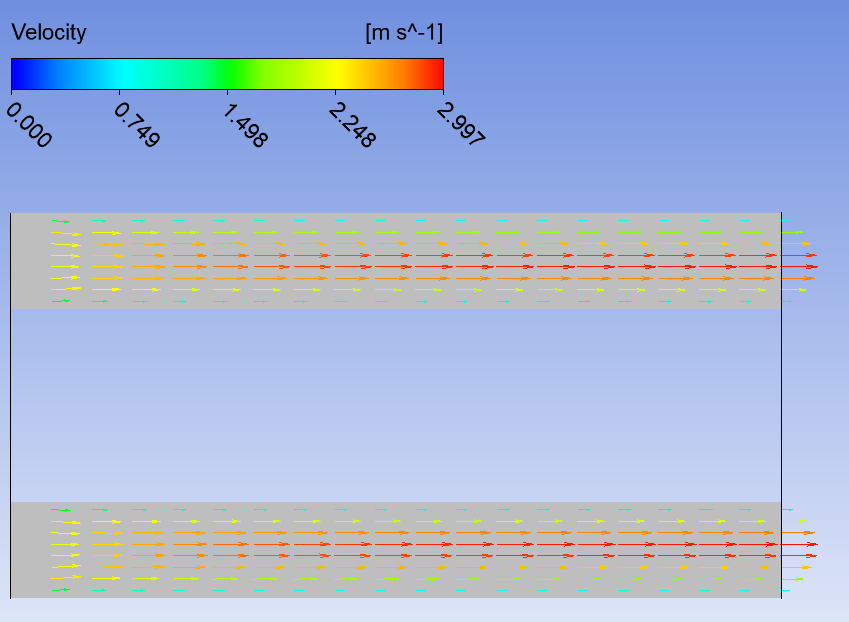 Рисунок 8 - векторное поле скоростей для Re = 200 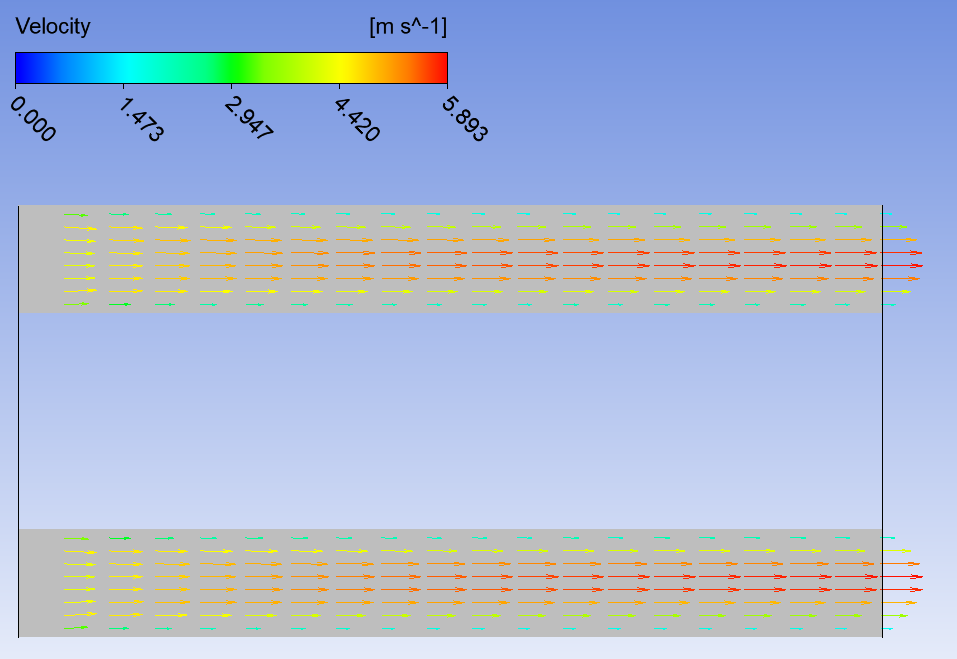 Рисунок 9 - векторное поле скоростей для Re = 400 Максимальные скорости потока для разных чисел Рейнольдса представлены в таблице 2. Таблица 2 – максимальные расчётные скорости потока
Профили скоростиНа рисунках ниже представлены профили скоростей для разных чисел Рейнольдса для половины сечения тубы. 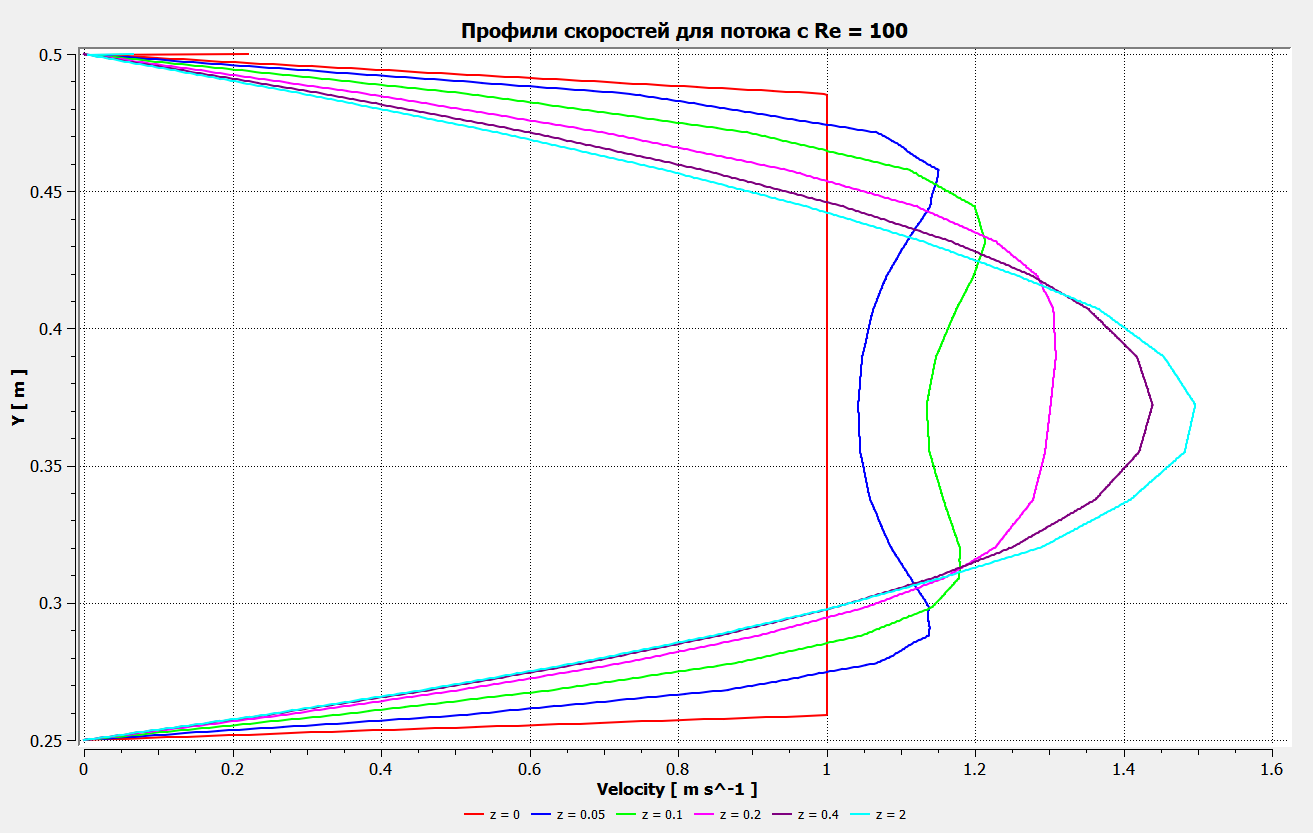 Рисунок 10 - профили скоростей для Re = 100 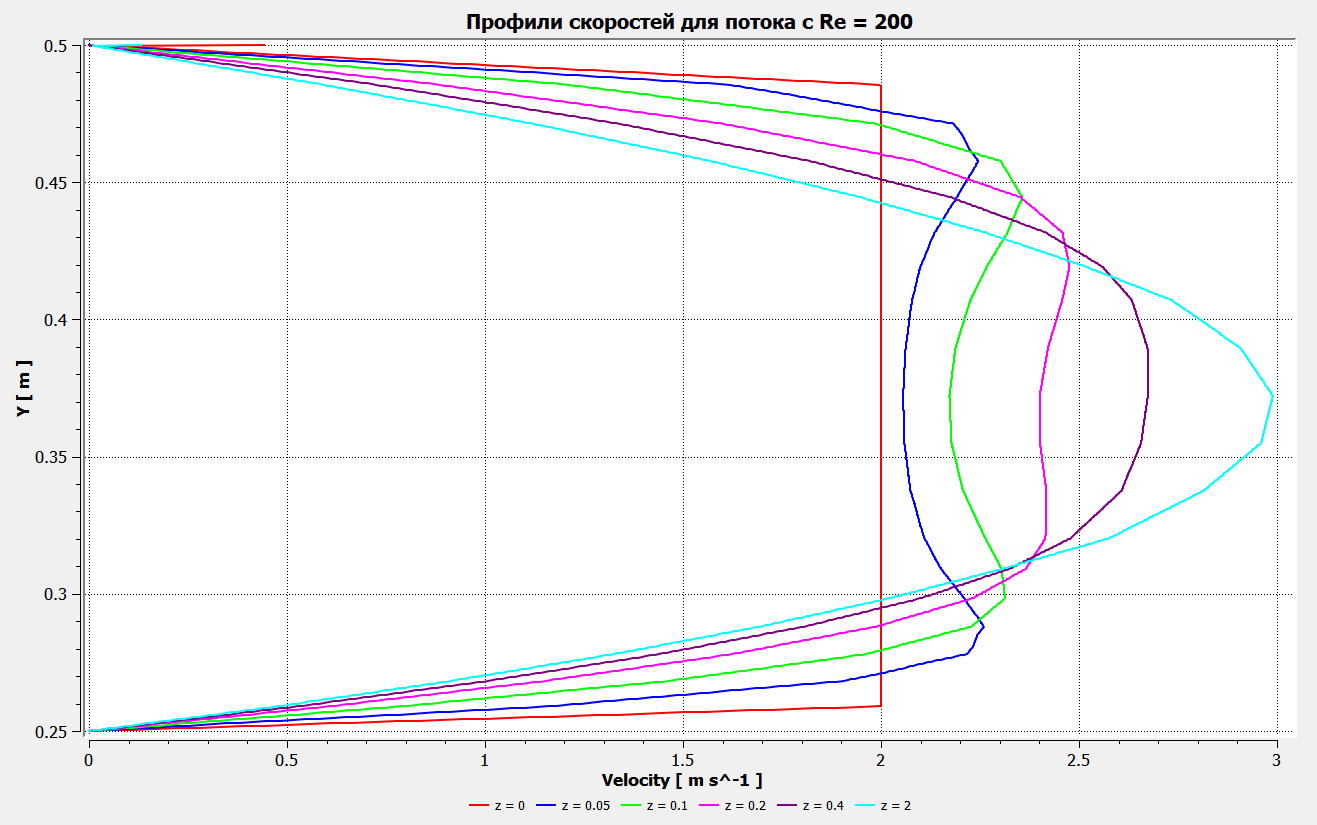 Рисунок 11 - профили скоростей для Re = 200 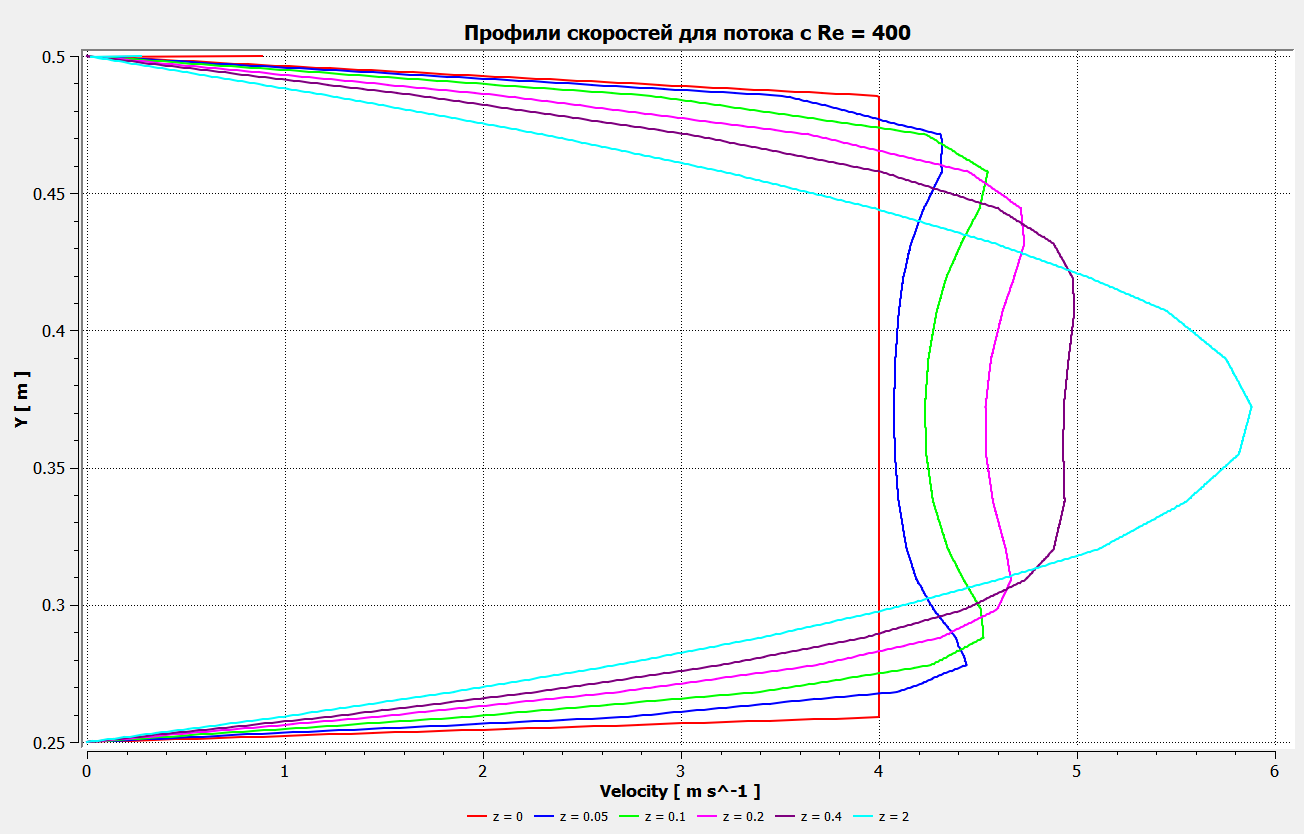 Рисунок 11 - профили скоростей для Re = 400 Из графиков видно, что на вход задаётся поток скорости равный расчётному значению, следуя далее по каналу он приобретает М-образную форму, а затем приобретает вид параболы Пуазейля. Графики скоростей, давления и касательных напряженийНа рисунках ниже представлен графики распределения максимальных скоростей, давления и касательных напряжений по всей длине трубы вдоль проекции серединной цилиндрической поверхности трубы, изображённой на рисунке 12 (далее упоминаемой как средняя линия течения).  Рисунок 12 – линия сбора исследуемых показателей расчёта 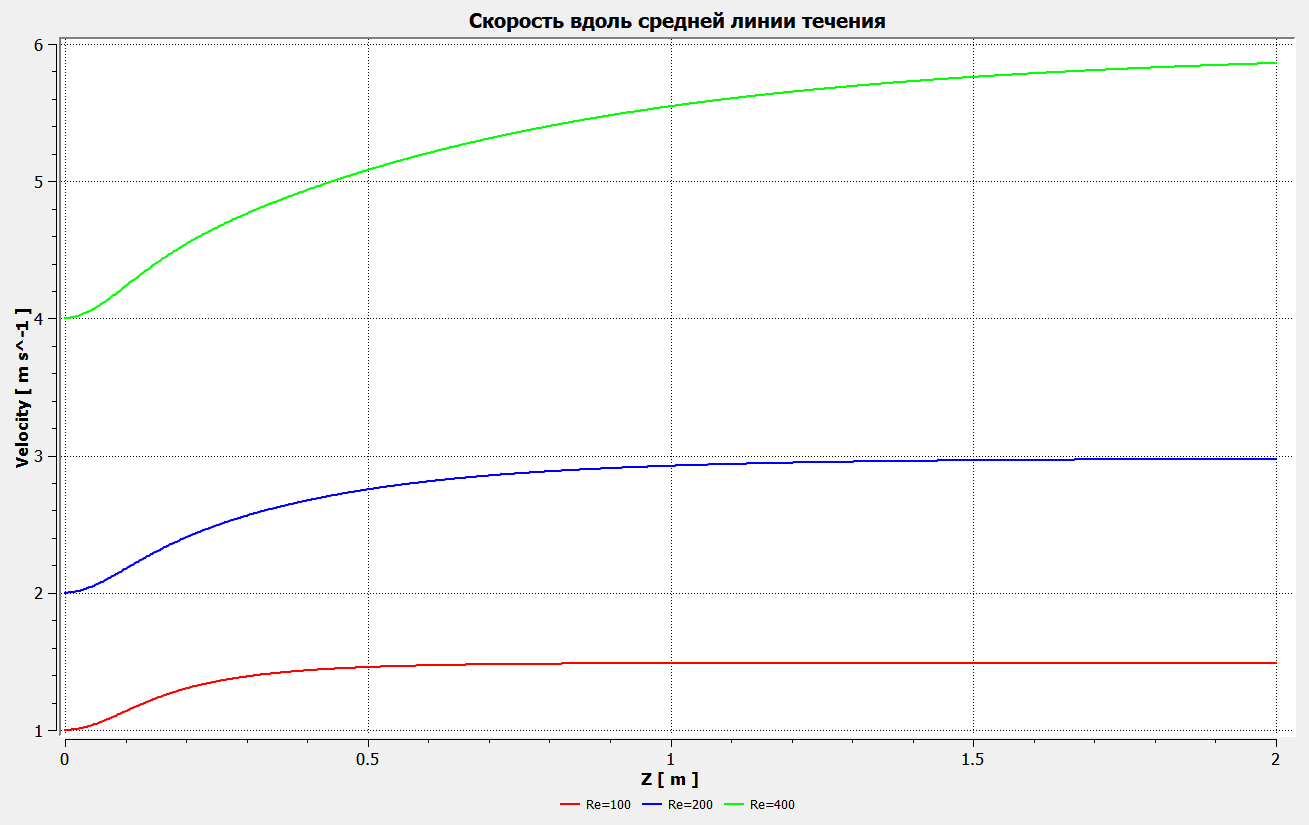 Рисунок 13 – распределение скоростей потоков вдоль средней линии течения. 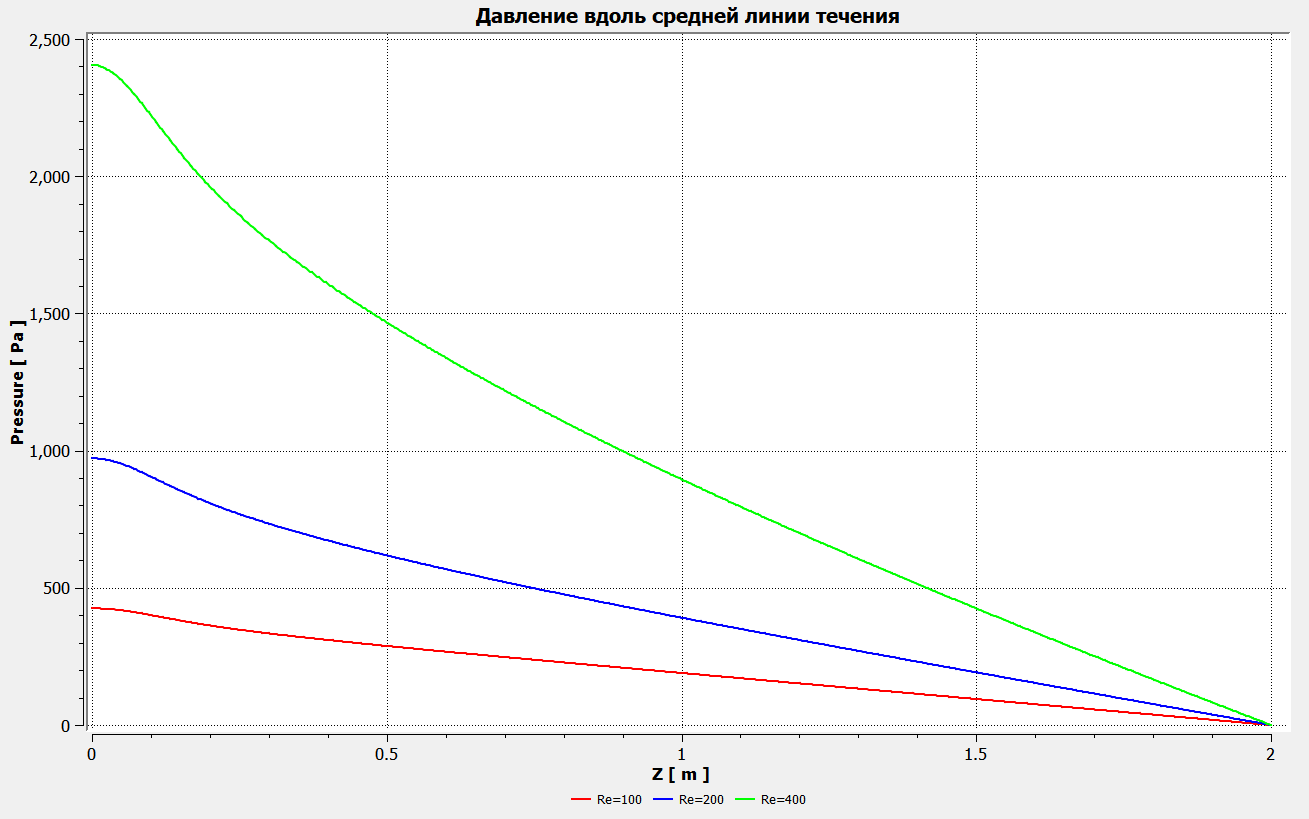 Рисунок 14 – распределение давления вдоль средней линии течения. 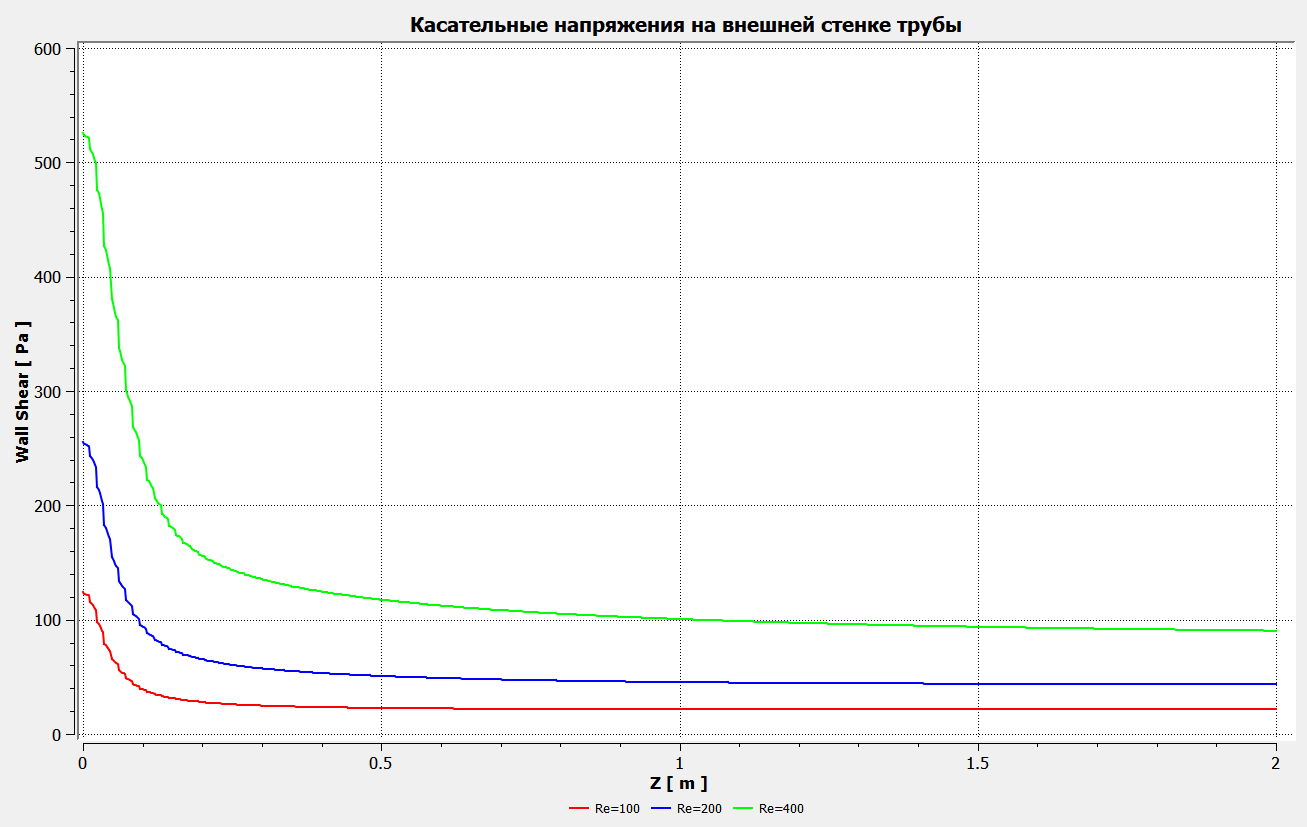 Рисунок 15 - распределение касательных напряжений на внутренней стенке трубы вдоль средней линии течения. 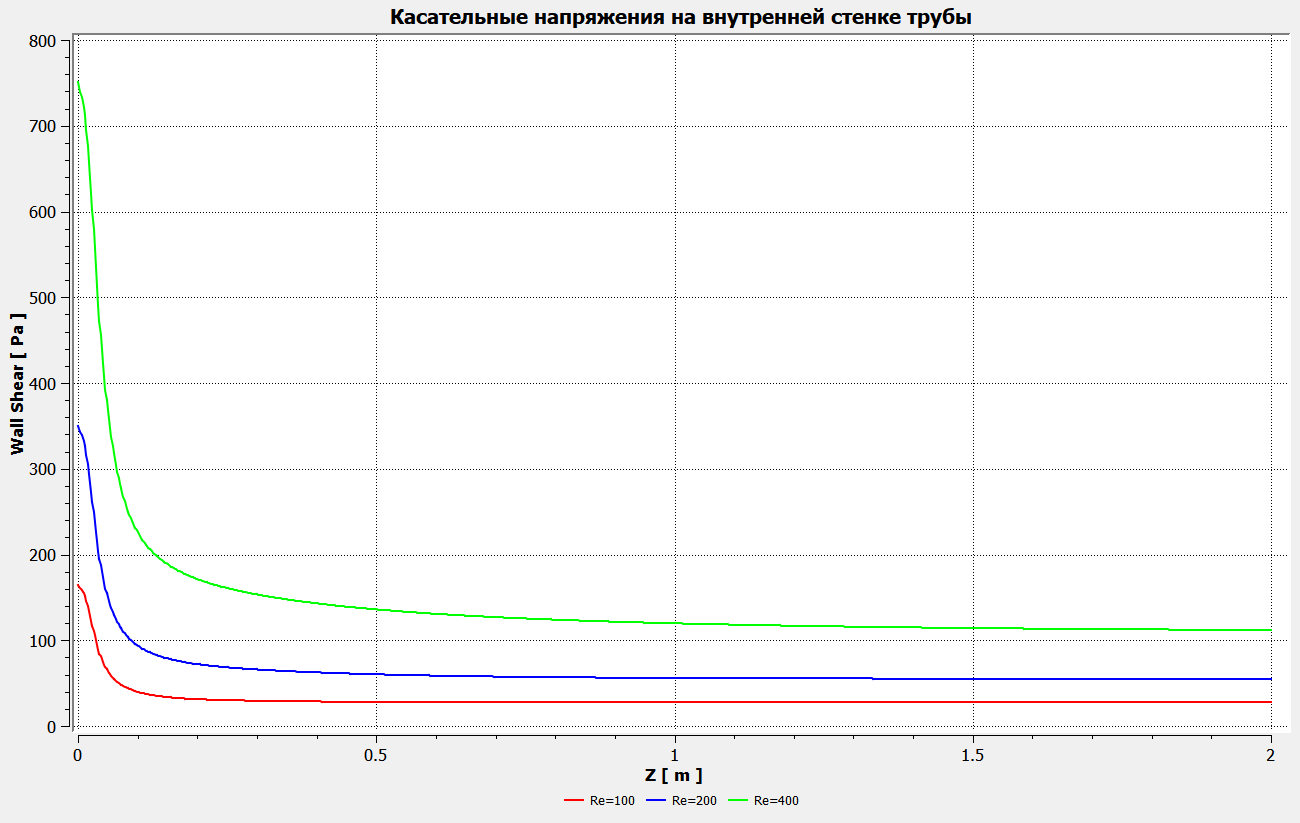 Рисунок 15 - распределение касательных напряжений на внутренней стенке трубы вдоль средней линии течения. Из полученных графиков скорости можно определить длину начального участка, как расстояние от входа до места, где скорость потока составляет 98% от максимальной. Для Re=100 длина начального участка состаляет примерно 0.78 м. Для Re=200 – примерно 1.2 м. Для Re=400 течение при длине трубы 2 м не успело стать установившимся. Удлинение трубы для более подробного изучения потока с Re=400 осложнено ограничениями студентческой версии ANSYS по количеству элементов. Из графиков распределения касательных напряжений на внешней и внутренней стенках трубы можно заметить, что на входе напряжения на внешней стенке трубы значительно меньше напряжений на внутренней стенке, однако на установившемся участке значения напряжений становятся близкими. Данная ассиметрия на входе наиболее ярко заметна на поле скоростей: 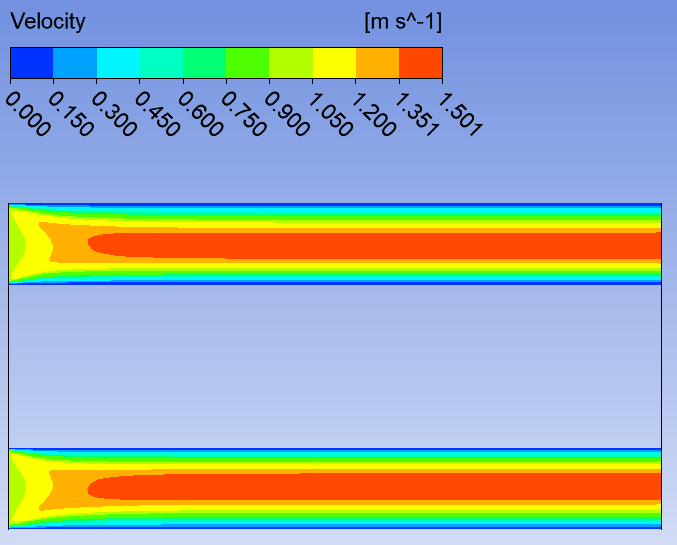 Рисунок 16 – поле скоростей для Re=100 Сравнение аналитического решения с полученным в программе ANSYS FluentАналитические решение для скорости в установившемся течении , а также для средней скорости вычисляются по формуле: 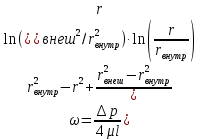 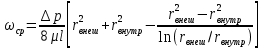 где 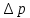 — разница давлений (рассчитывается для участка с установившимся течением); — разница давлений (рассчитывается для участка с установившимся течением); 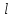 — длина исследуемого участка с установившемся течением (для длины начального участка взято значение рассчитанное в ANSYS за неимение точной расчётной формулы); — длина исследуемого участка с установившемся течением (для длины начального участка взято значение рассчитанное в ANSYS за неимение точной расчётной формулы);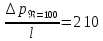 Па/м. Па/м.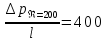 Па/м. Па/м.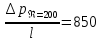 Па/м. Па/м.Тогда, учитывая параболическую форму профиля скорости на установившемся течении, аналитические значения скорости для потоков: Re=100: 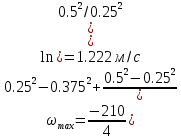 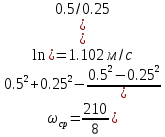 Re=200: 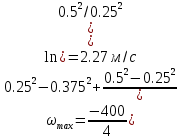 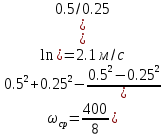 Re=400: 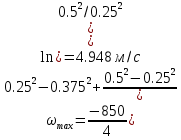 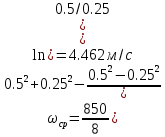 Таблица 3 – сравнение расчётных и аналитических значений скоростей потока для разных чисел Рейнольдса
где Vmax – расчётная максимальная скорость, 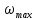 — аналитически найденная максимальная скорость потока, — аналитически найденная максимальная скорость потока, 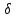 – погрешность. – погрешность.Таблица 4 – сравнение расчётных и аналитических значений средних скоростей потока для разных чисел Рейнольдса
где Vср – расчётная максимальная скорость, 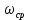 — аналитически найденная максимальная скорость потока, — аналитически найденная максимальная скорость потока, 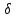 – погрешность. – погрешность.Данные решения можно назвать только приближенными в связи с тем, что некоторые величины рассчитаны не аналитическим способом. Полученные значения максимальной скорости получились достаточно точными, погрешность не превышает 11%. Теоретические значения коэффициентов сопротивления 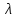 определялись по формуле [2]: определялись по формуле [2]: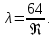 Тогда: 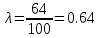 — для Re=100. — для Re=100.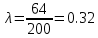 — для Re=200. — для Re=200.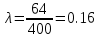 — для Re=400. — для Re=400.Численное значение коэффициента сопротивления 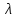 определялось по формуле с использованием значений, полученных в Ansys CFD-Post: определялось по формуле с использованием значений, полученных в Ansys CFD-Post: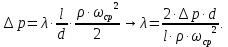 где 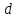 — гидравлический диаметр трубы (d = dвнеш – dвнутр); — гидравлический диаметр трубы (d = dвнеш – dвнутр); 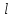 — длина исследуемого участка с установившемся течением; — длина исследуемого участка с установившемся течением; 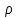 — плотность; — плотность; 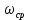 — средняя скорость потока, рассчитываемая по формуле: — средняя скорость потока, рассчитываемая по формуле:Тогда расчётный коэффициент сопротивления для исследуемых чисел Рейнольдса: Re=100: 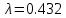 Re=200: 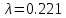 Re=400: 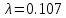 Таблица 4 – сравнение расчётных и аналитических значений коэффициентов сопротивления потока для разных чисел Рейнольдса
где 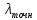 – расчётный коэффициент сопротивления потока, – расчётный коэффициент сопротивления потока, 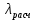 — аналитически найденный коэффициент сопротивления потока, — аналитически найденный коэффициент сопротивления потока, 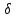 – погрешность. – погрешность.ВыводВ данной работе был проведён численный расчет стационарного ламинарного течения вязкой несжимаемой жидкости в трубки кольцеобразного сечения для разных значений числа Рейнольдса: 100, 200, 400 с использованием расчётной программы Fluent. Были построены геометрия, расчётная сетка, проанализированы поля скоростей в потоке, профили скорости и построены распределения давления и касательных напряжений на внутренней и внешней стенках трубы. Были рассчитаны и вычислены аналитически средняя скорость (максимальная погрешность составила 11%), максимальная скорость (максимальная погрешность составила 22%), а также коэффициент сопротивления потока (максимальная погрешность составила 33%). Список литературыЛойцянский Л. Г. (1950). Механика жидкости и газа. Ленинград: Гоосударственное издательство технико-теоретической литературы. |

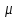 , Па с
, Па с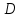 , м
, м