математика. Числовые характеристики

• Название: Числовые характеристики
• Анкор: математика
• Дата: 14.06.2022
• Размер: 127.76 Kb.
• Имя файла: Лекция 21. Характеристики св.docx
• Тип: Закон; #589845

Числовые характеристики

Для описания случайной величину как дискретных, так и непрерывных используются числовые характеристики, которые дают представление о случайной величине без знания закона распределения случайной величины.

1. 
   Математическое ожидание.
   

Обозначаем M(x). Это число, которое указывает на возможное среднее значение случайной величины.

Формулы нахождения.

Для ДСВ: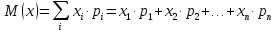

Для НСВ:

f(x) - плотность распределения (как правило задана, или находят от F’(x) = f(x) как производную от функции распределения; a,b – крайние возможные значения х.

Свойства М(х):

1. 
   М(с) =с, с=соnst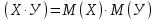
   
2. 
   М (сх) = с М(х)
   
3. 
   М
   
4. 
   М
   

2. 
   Дисперсия.
   

Обозначаем D(x). Это число, которое характеризует степень отклонения значения случайной величины от математического ожидания случайной величины (степень разброса).

Формулы нахождения.

Для ДСВ: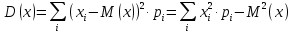

Для НСВ: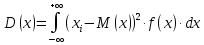

f(x) - плотность распределения (как правило задана, или находят от F’(x) = f(x) как производную от функции распределения; a,b – крайние возможные значения х.

Свойства D(х):

1. 
   D(с) =0, с=соnst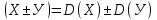
   
2. 
   D (х)
   
3. 
   D (сх) = D(х)
   
4. 
   D
   

3. 
   Дисперсия.
   

Обозначаем (x). Это число, которое характеризует насколько в среднем значения случайной величины от математического ожидания.

Формула нахождения. (x)=

Примеры:

1. 
   ДСВ задана законом распределения.
   

	2	3	6	7	8	10
	0,1	0,2	0,25	0,2	0,15	0,1

Построить многоугольник распределения. Найти М(х), D(x), 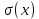. Вычислить вероятность события 0 .

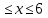Решение: Это дискретная случайная величина. Используем формулы для дискретной случайной величины. Подставляем в формулу: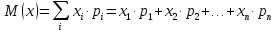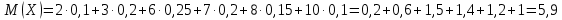



Подставляем в формулу: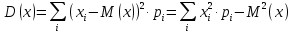



Подставляем в формулу: (x)=

(x)=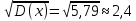

р (0 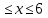)=0,1+0,2+0,25=0,55=55%



График представляет из себя ломаную, масштаб надо брать удобный для данной задачи, но по оси у э то всегда будет промежуток от 0 до 1.

2. 
   Случайная величина задана плотностью вероятности:
   

Найдите М(х), D(x),

Решение: Это непрерывная случайная величина. Используем формулы для непрерывной случайной величины. Подставляем в формулу: . Так как на двух промежутках значение f(x) равно 0.



Подставляем в формулу: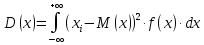