Решение задач по высшей математике. Вариант 3. Чудова межа

• Название: Чудова межа
• Анкор: Решение задач по высшей математике
• Дата: 22.12.2022
• Размер: 344.75 Kb.
• Имя файла: Вариант 3.docx
• Тип: Документы; #858735

Завдання №1

Пункт 1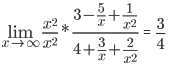




Пункт 2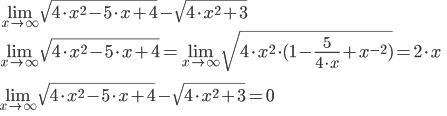



Пункт 3


II чудова межа

 =   =   =   = 
a = -6, b = 5/3



Пункт 4








Завдання №2

Пункт 1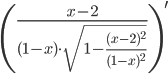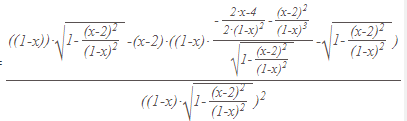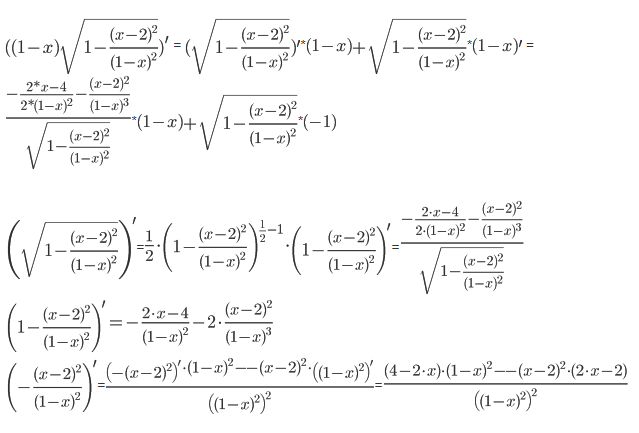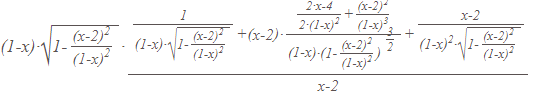


=







Пункт 2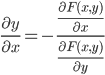






Пункт 3

x=t-sin(t)
y=1+cos(t)




x_t' = 1-cos(t)
y_t' = -sin(t)



Пункт 4

y=(2·x)^tg(x)


y^′=(2·x)^tg(x)·(ln(2·x)·tg(x))^′


(2·x)^′=2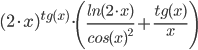



Завдання №3

z = (3*x*y^2-3*y*x^2+5*y)^4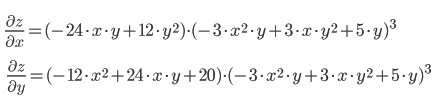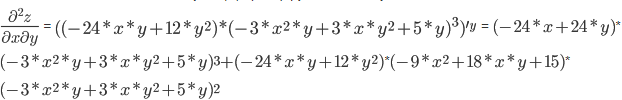



Завдання №4
1) Область визначення функції. Точки розриву функції .
2) парність або непарність функції .

Функція загального виду
3) Періодичність функції .
4) Точки перетину кривої з осями координат .
Перетин з віссю 0Y

x=0, y=3


Перетин з віссю 0X
y = 0


5) Дослідження на екстремум .
y = (2*x^2-6)/(x-2)
Знайдемо точки розриву функції.

x ₁ = 2


1. Знаходимо інтервали зростання та спадання . Перша похідна.

або

Знаходимо нулі функції. Для цього прирівнюємо похідну до нуля

2 · x ² -8 · x +6 = 0


Звідки:

x ₁ = 1
x ₂ = 3

(-∞ ;1)	(1; 2)	(2; 3)	(3; +∞)
f'(x) > 0	f'(x) < 0	f'(x) < 0	f'(x) > 0
функція зростає	функція зменшується	функція зменшується	функція зростає

На околиці точки x = 1 похідна функції змінює знак з (+) на (-). Отже, точка x = 1 – точка максимуму. На околиці точки x = 3 похідна функції змінює знак з (-) на (+). Отже, точка x = 3 – точка мінімуму.
2. Знайдемо інтервали опуклості та увігнутості функції . Друга похідна.

або

Знаходимо коріння рівняння. Для цього отриману функцію прирівняємо до нуля.

Для цього рівняння коріння немає.

(-∞ ;2)	(2; +∞)
f''(x) < 0	f''(x) > 0
функція опукла	функція увігнута

6) Асимптоти кривої .

Рівняння похилих асимптот зазвичай шукають як y = kx + b. За визначенням асимптоти:

Знаходимо коефіцієнт k:


Знаходимо коефіцієнт b:


Отримуємо рівняння похилої асимптоти:

y = 2·x+4


Знайдемо вертикальні асимптоти. Для цього визначимо точки розриву:

x ₁ = 2


Знаходимо переділи в точці x = 2


x ₁ = 2 - точка розриву ІІ роду і є вертикальною асимптотою.

Знайдемо похилу асимптоту при x → -∞:

Знаходимо коефіцієнт k:


Знаходимо коефіцієнт b:


Отримуємо рівняння похилої асимптоти:

y = 2·x+4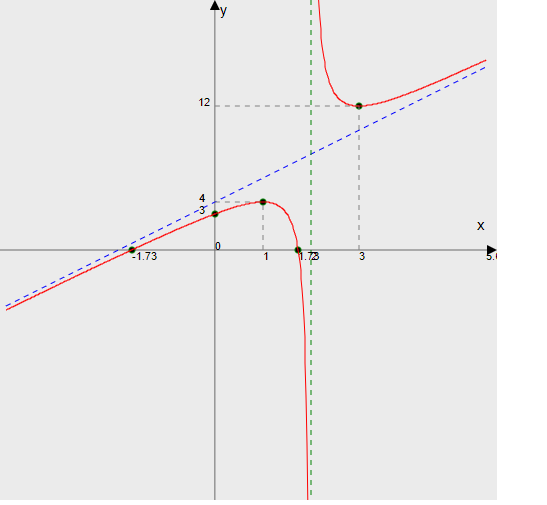



Завдання №5
z = 3-2*x^2-y^2-x*y
1. Знайдемо приватні похідні .


2. Вирішимо систему рівнянь .
-4*xy = 0
-x-2*y = 0
Отримаємо:
а) З першого рівняння виражаємо x і підставляємо у друге рівняння:
x = -2*y
7*y = 0
Звідки y = 0
Дані значення y підставляємо у вираз для x . Отримуємо: x = 0
Кількість критичних точок дорівнює 1.
M ₁ (0; 0)
3. Знайдемо приватні похідні другого порядку .



4. Обчислимо значення цих похідних приватних другого порядку в критичних точках M(x ₀ ;y ₀ ).
Обчислюємо значення точки M ₁ (0;0)



AC - B ² = 7 > 0 і A < 0 , то точці M ₁ (0;0) є максимум z(0;0) = 3
Висновок : У точці M ₁ (0; 0) є максимум z (0; 0) = 3;