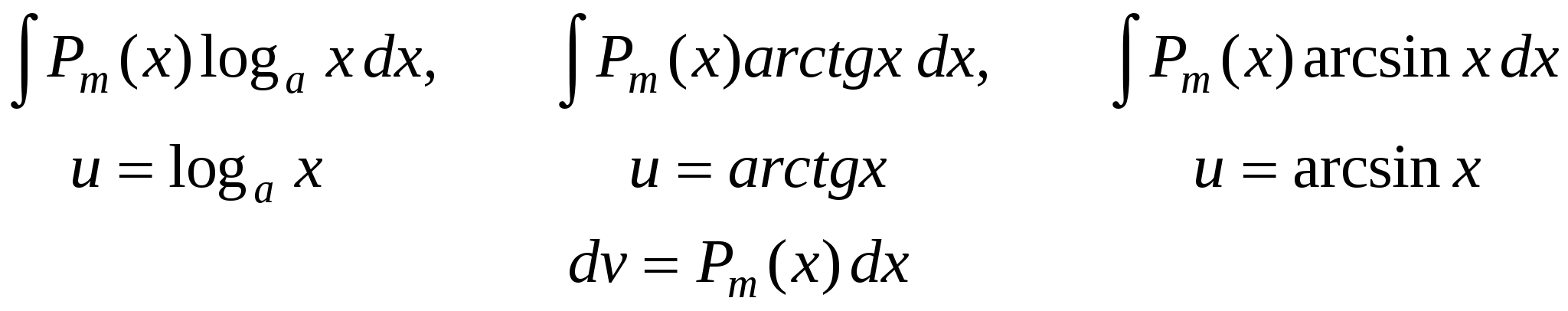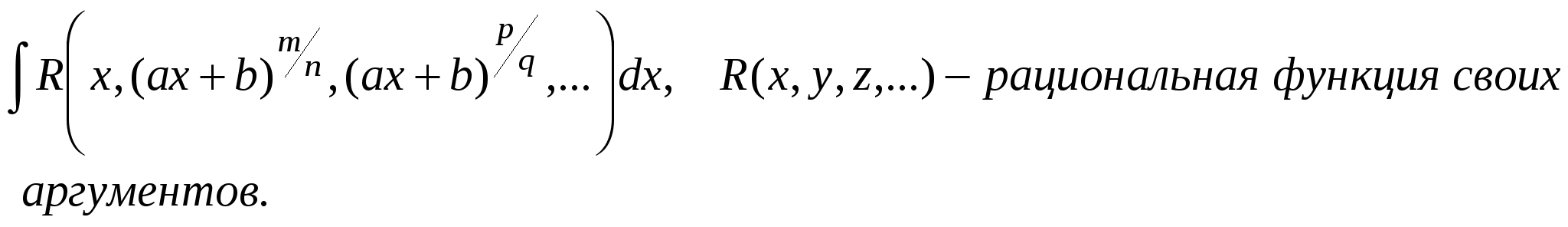Неопределенныйинтеграл. Дана функция f
 Скачать 272 Kb. Скачать 272 Kb.
|
|
Неопределенный интеграл. Дифференциальное исчисление решает следующую задачу: дана функция F(x), найти ее производную f(x). F 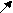 ′(x) = f(x). ′(x) = f(x).найти Интегральное исчисление решает обратную задачу: дана функция f(x), найти такую функцию F(x), производная от которой равна f(x). F 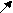 ′(x) = f(x) ′(x) = f(x)дана Определение. Первообразной от функции f(x) называется такая функция F(x), производная которой равна f(x). Например, f(x) = 3x2 , тогда F(x) = x3, (x3)′ = 3x2. В качестве первообразной можно взять любую функцию вида x3 + C, т.к. (x3 + C)′ = 3x2. Теорема. Если функция имеет первообразную, то она имеет и бесконечное множество первообразных, причем любые две из них отличаются лишь постоянным слагаемым. Пусть F(x) и Φ(x) – любые две первообразные. Рассмотрим Θ(x) = F(x) – Φ(x). Докажем, что Θ(x) ≡ Const. Найдем Θ′(x) = F′(x) - Φ′(x) ≡ 0. Рассмотрим два значения аргумента a и х (а – фиксированное, х – произвольное). Определение. Множество всех первообразных функции f(x) называется неопределенным интегралом. ∫f(x)dx. Если f(x) – первообразная f(x), то ∫f(x) dx = F(x) + C. Свойства неопределенного интеграла. 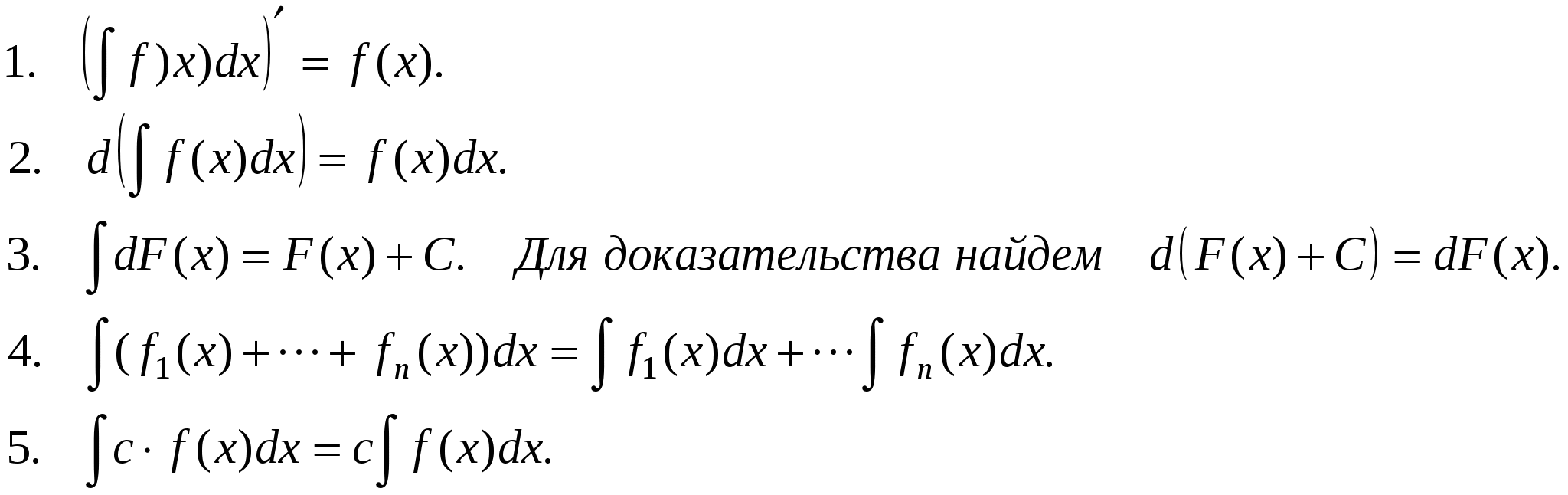 Таблица основных интегралов. 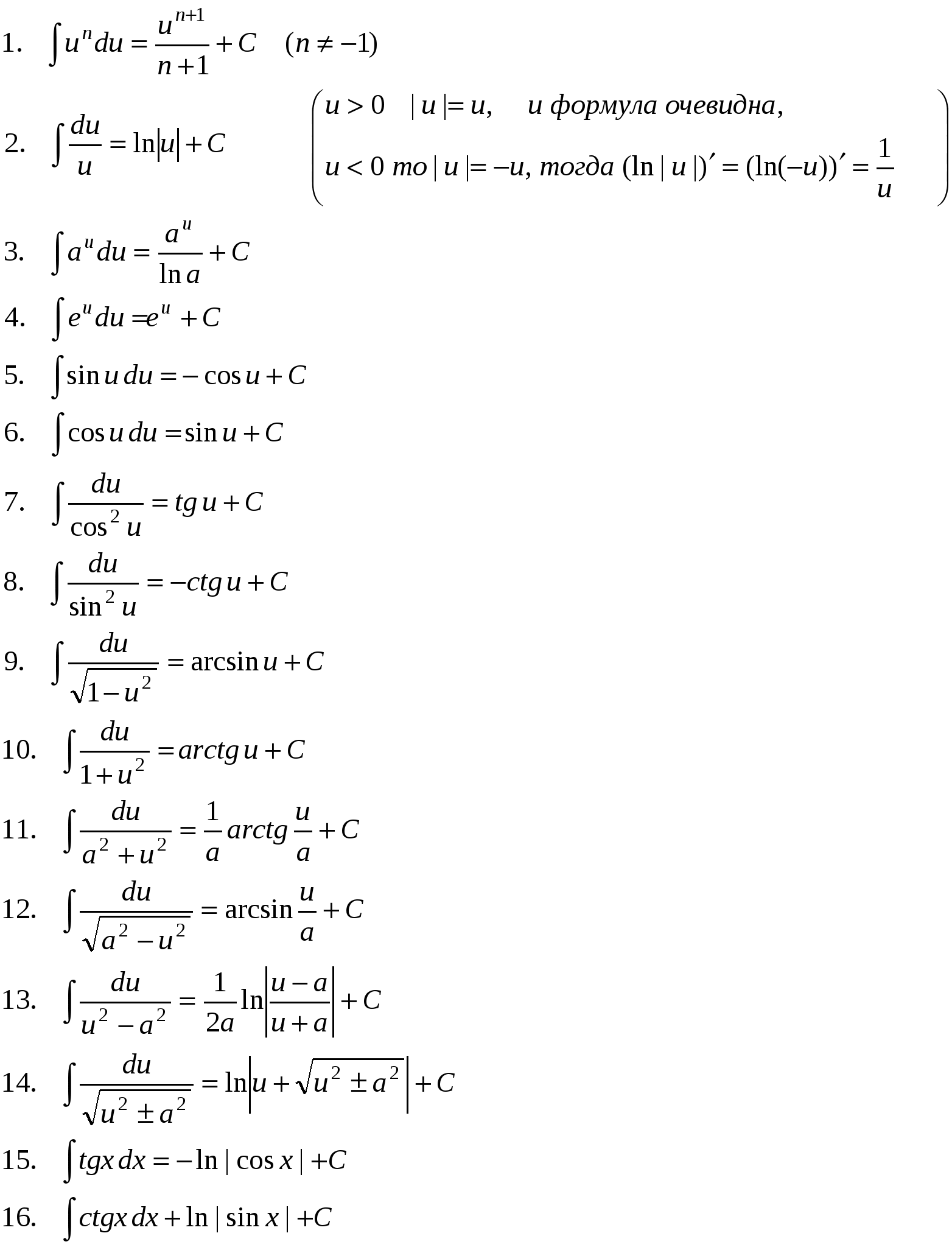 П    р и м е р ы. р и м е р ы.
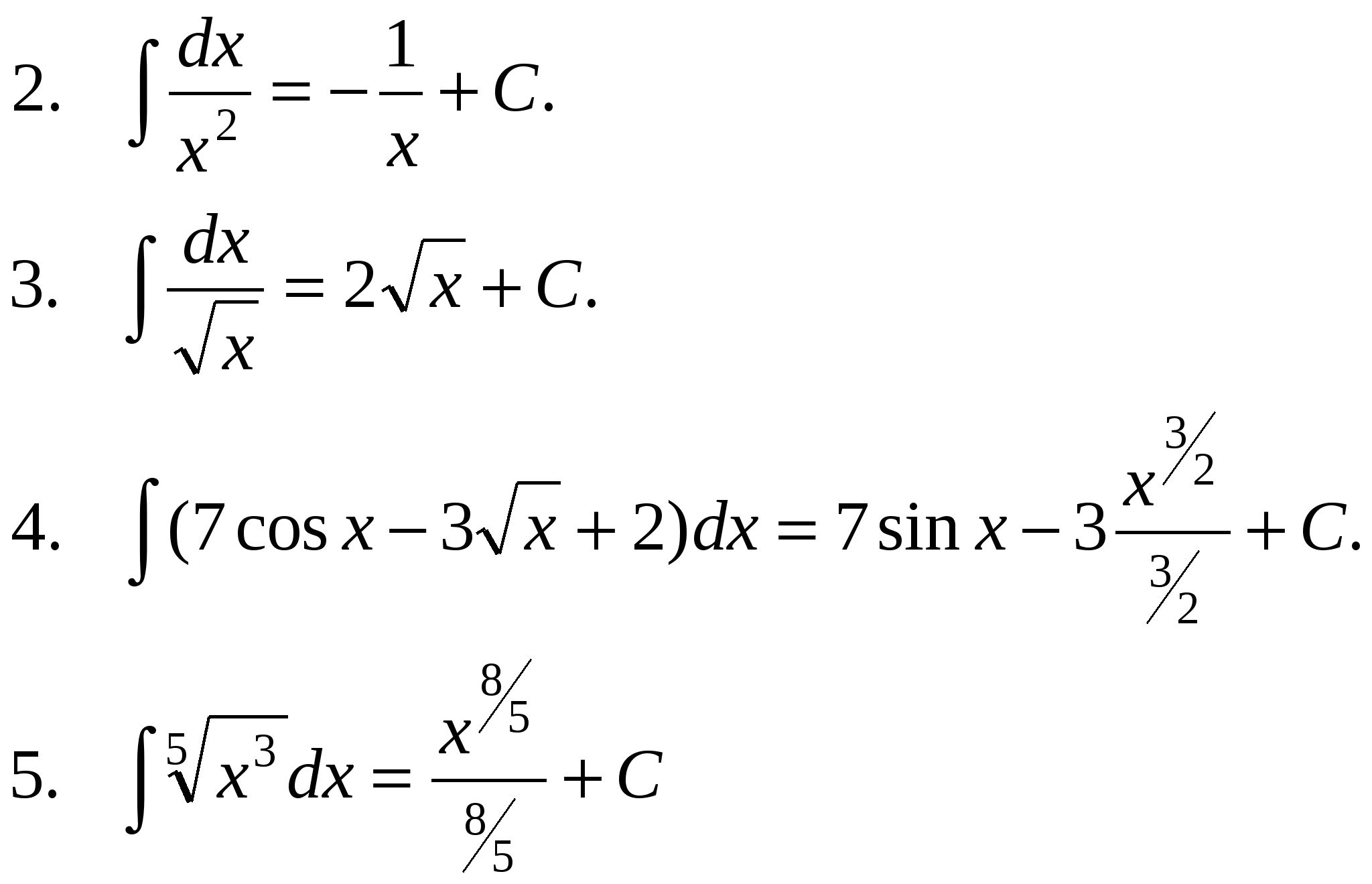  Основные методы интегрирования. Метод подстановки. Теорема. Если ∫ f(u)du = F(u) + C и u = φ(x) – любая дифференцируемая функция от x, то Доказательство. (F(φ(x)) + C)′ = F′(φ(x))∙φ′(x) = f(φ(x))∙φ′(x), т.к. F′(x) = f(x). Следствие. Если ∫ f(x)dx = F(x) + C, то ∫ f(kx)dx = 1/k F(kx) + C, ∫ f(kx + b)dx = 1/k F(kx + b) + C. Эта теорема позволяет расширить возможности таблицы основных интегралов. В этой таблице под u можно понимать любую функцию х. П р и м е р ы . 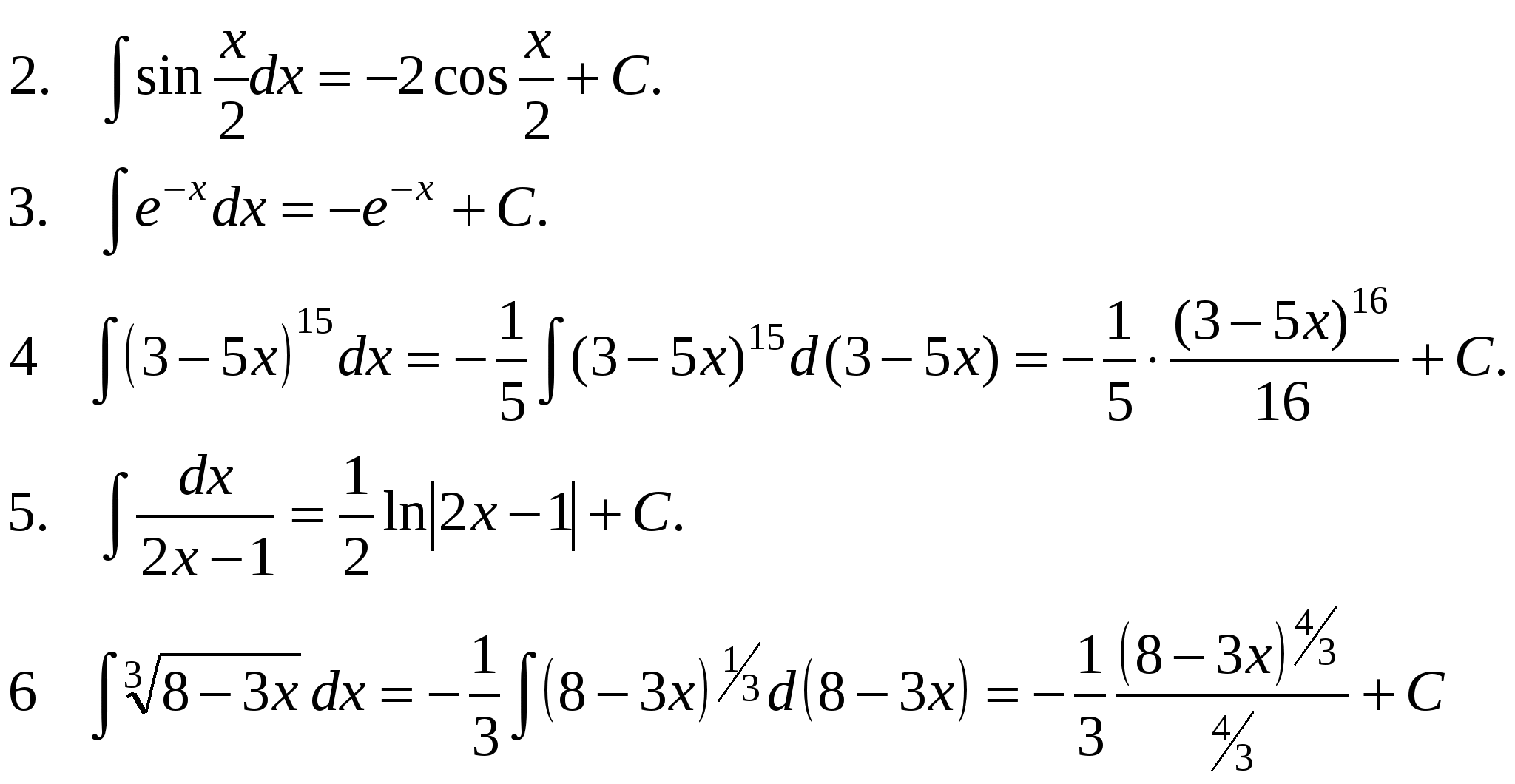 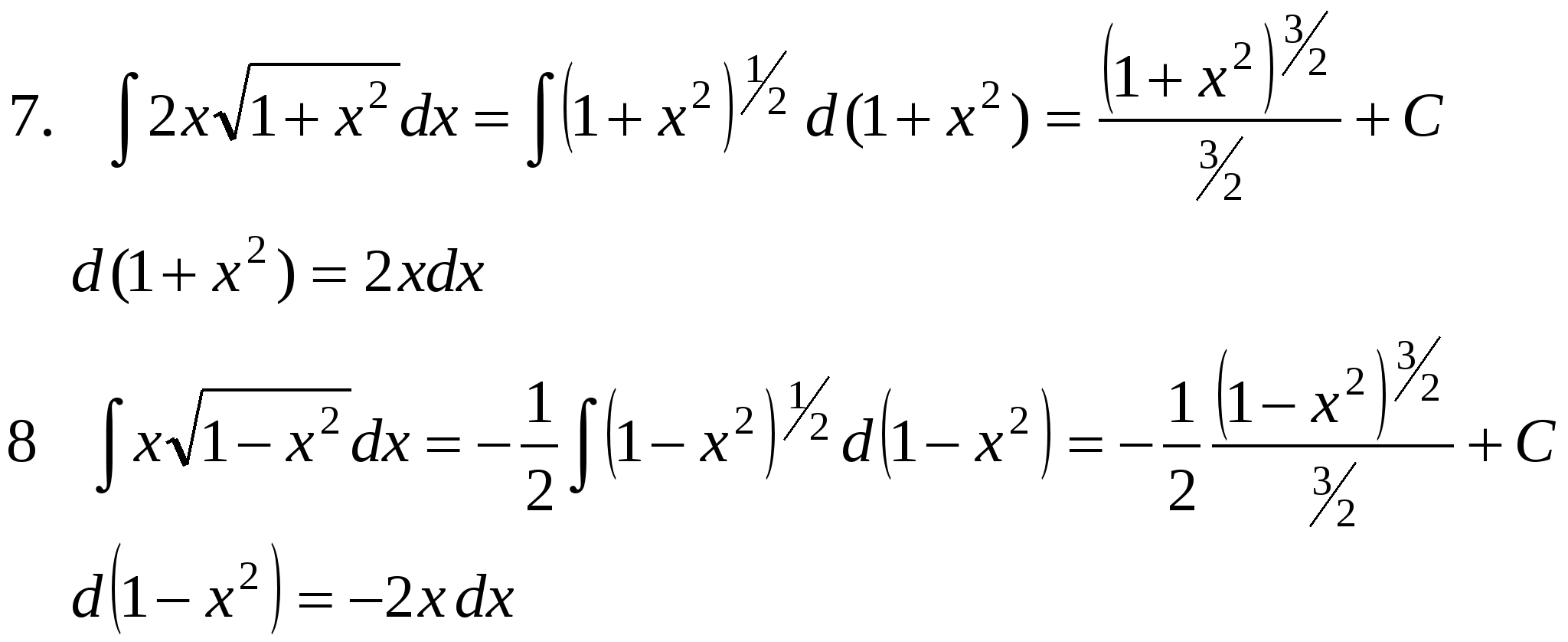 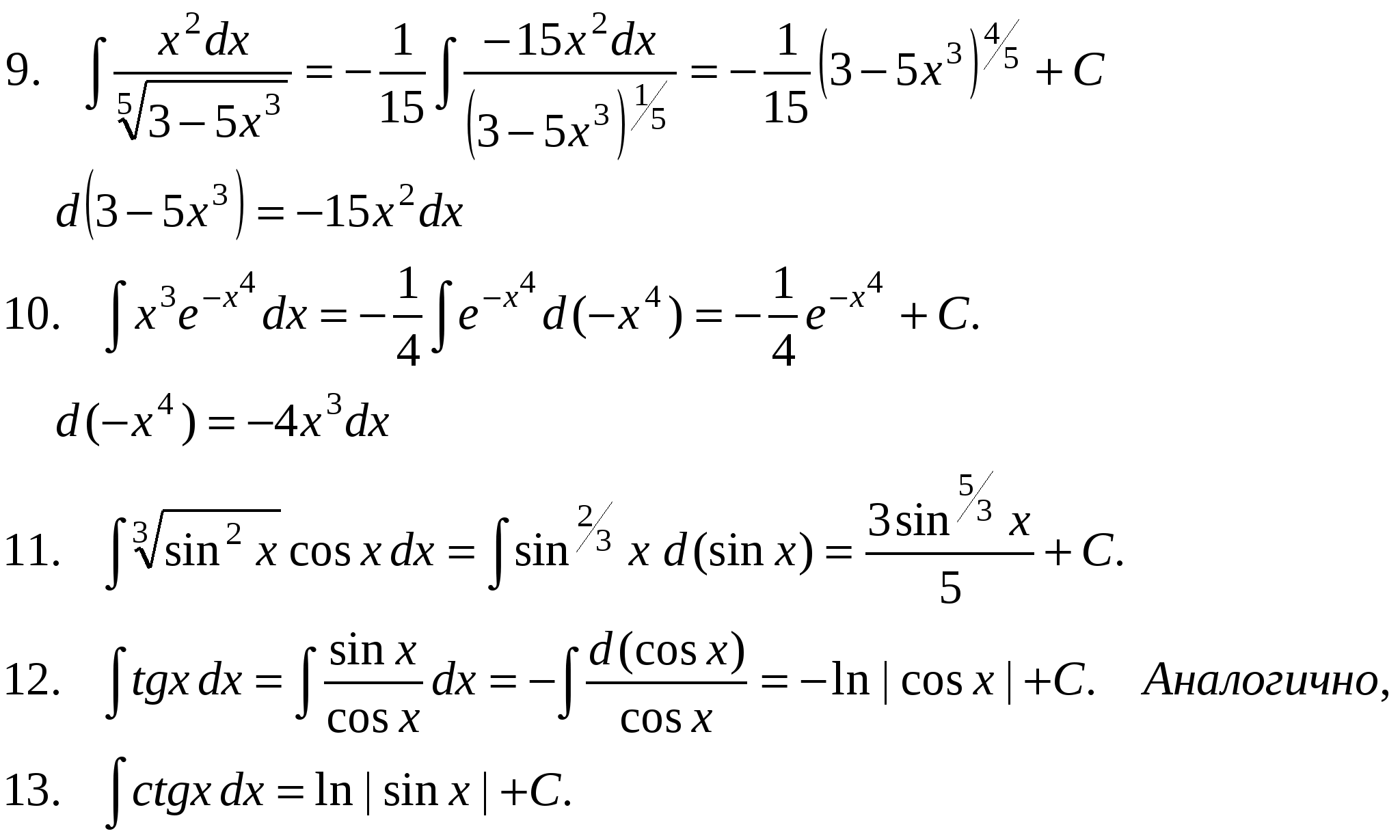 Интегралы от некоторых функций, содержащих квадратный трехчлен. 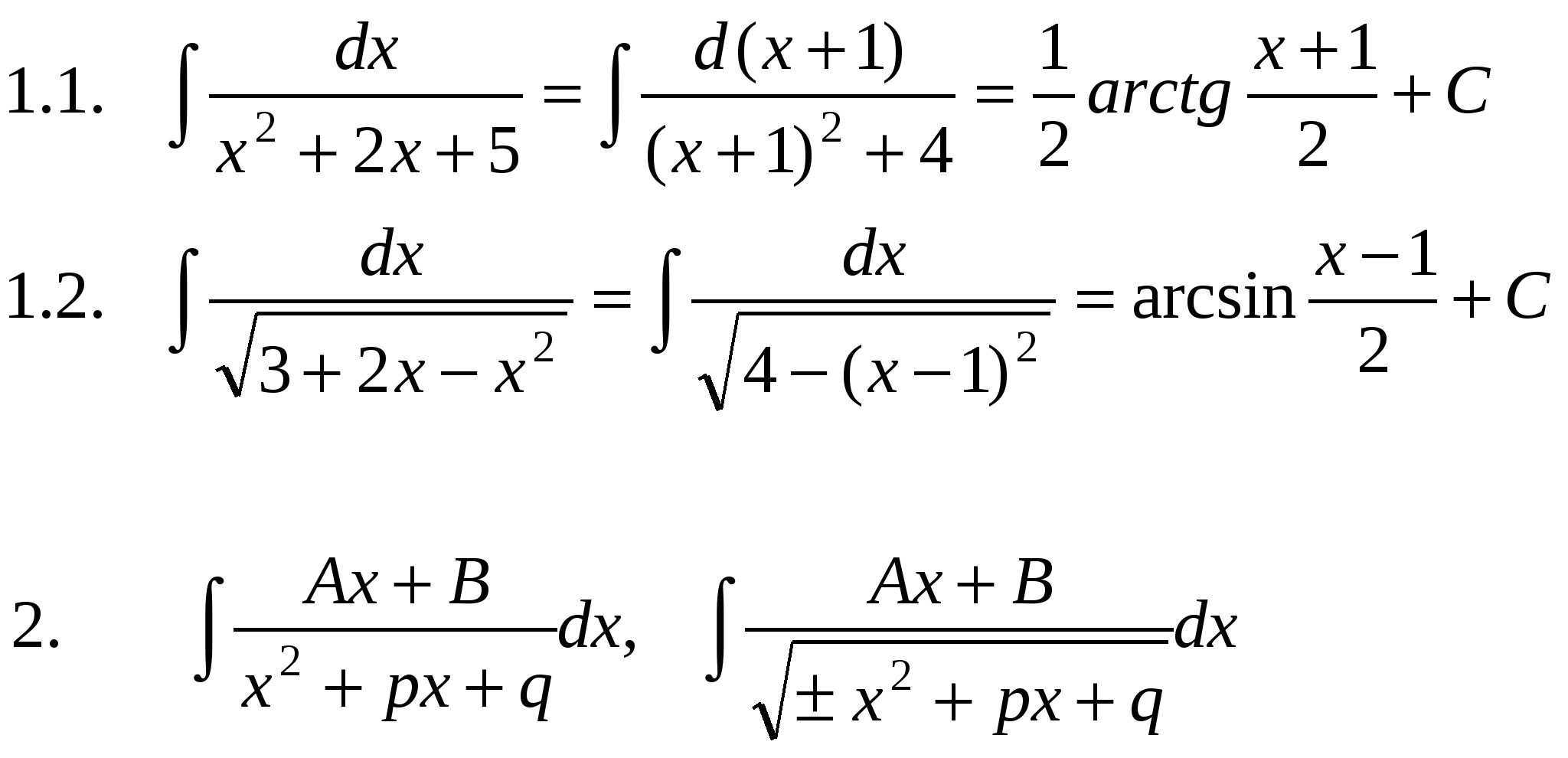 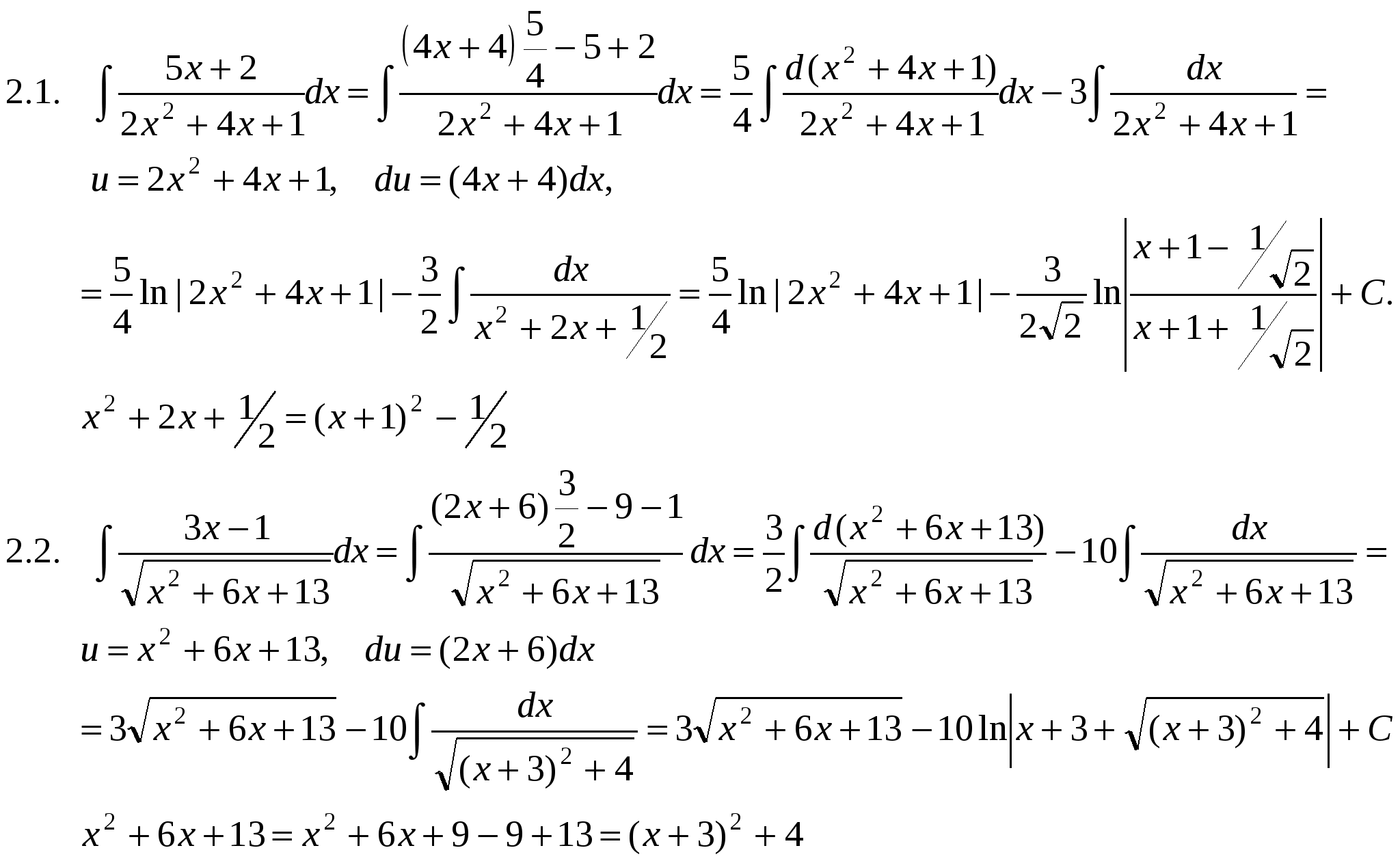 Интегрирование по частям. В интегрировании нет теоремы об интеграле произведения. В какой-то степени ее заменяет формула интегрирования по частям. Пусть u и v - дифференцируемые функции х. Тогда d(uv) = du v + u dv или udv = d(uv) – vdu Формула интегрирования по частям применяется в следующих случаях:
Pm(x) = a0xm + a1xm-1 +….+ am-1 x + am, u = Pm(x), dv= все остальное. П р и м е р ы . 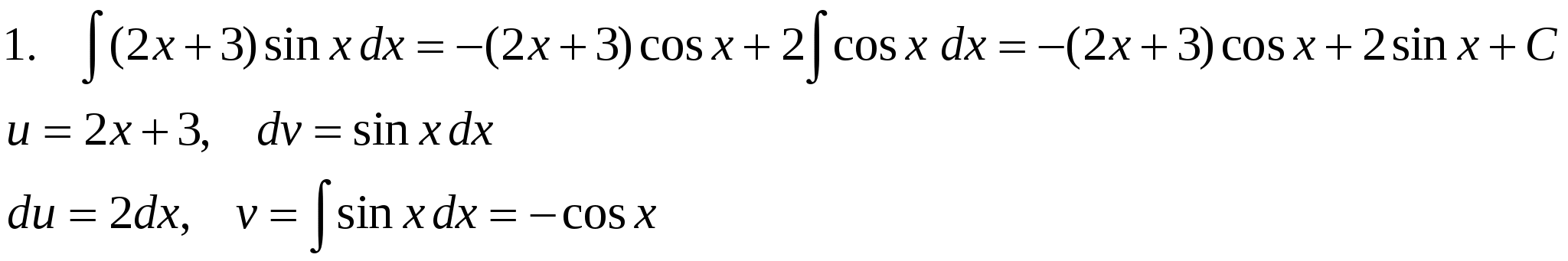 Иногда интегрирование по частям приходится применять несколько раз. 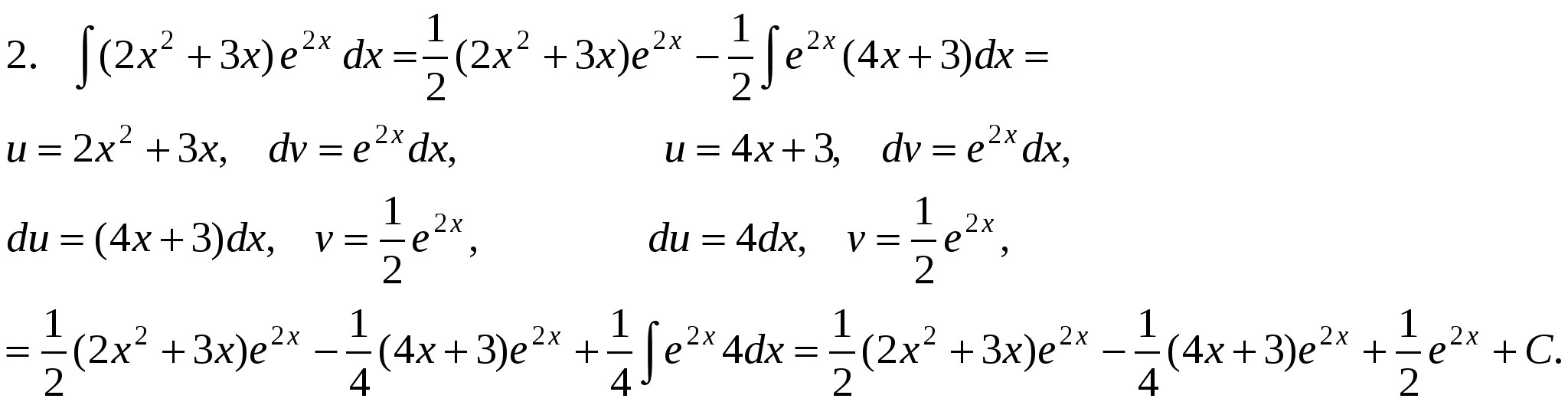 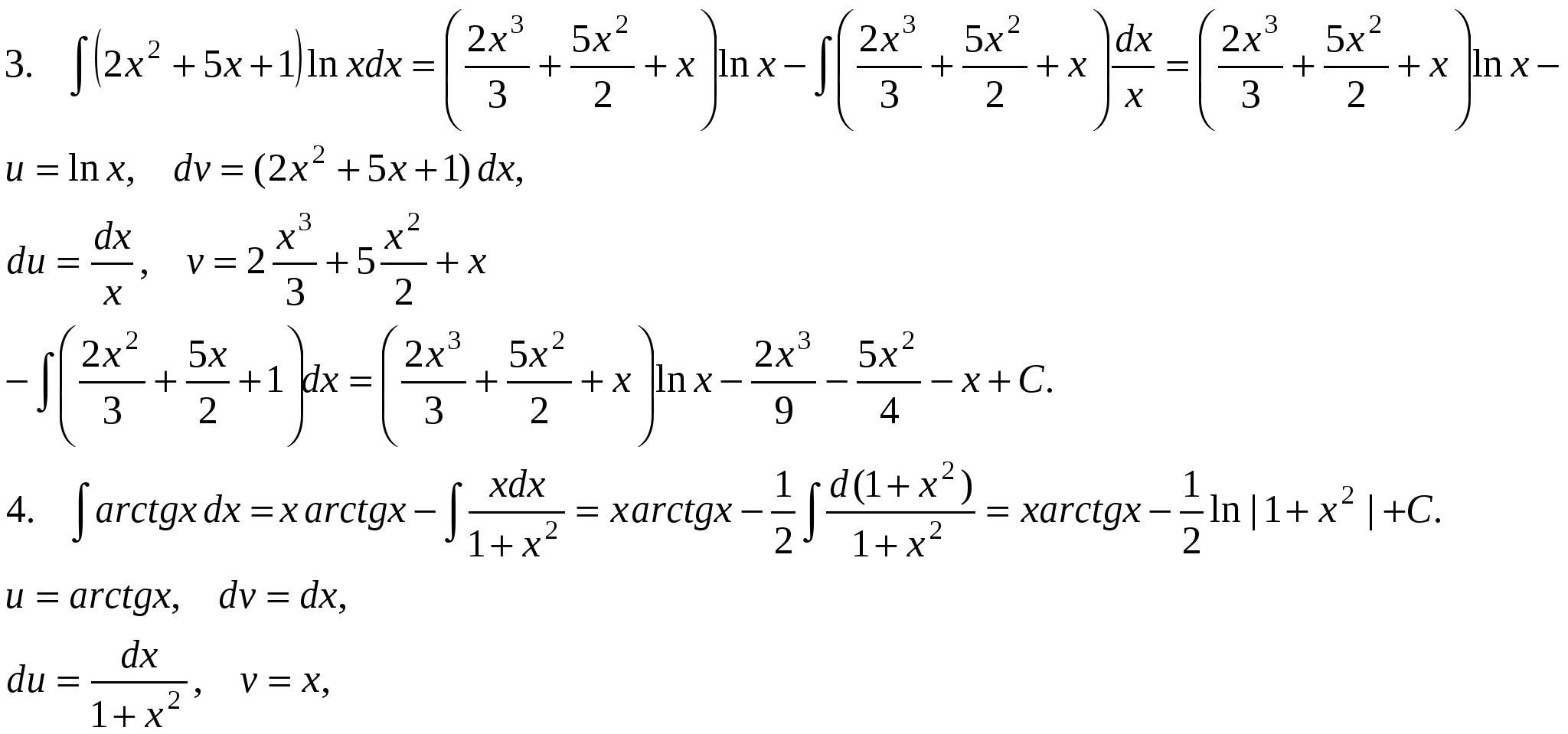 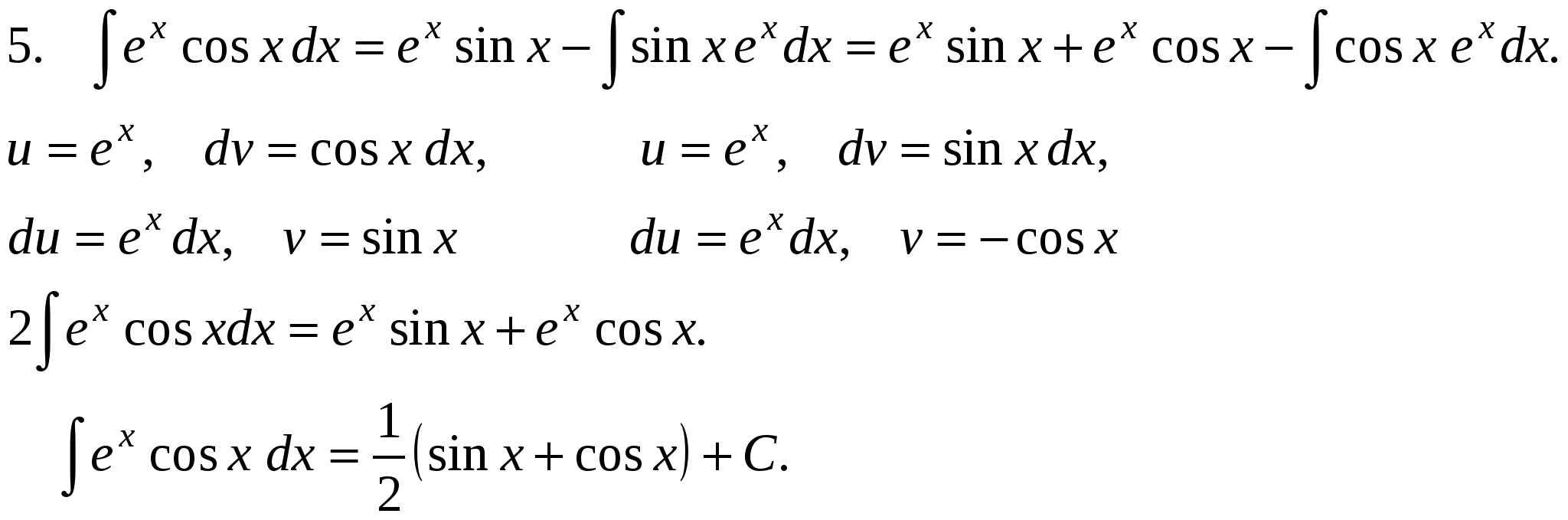 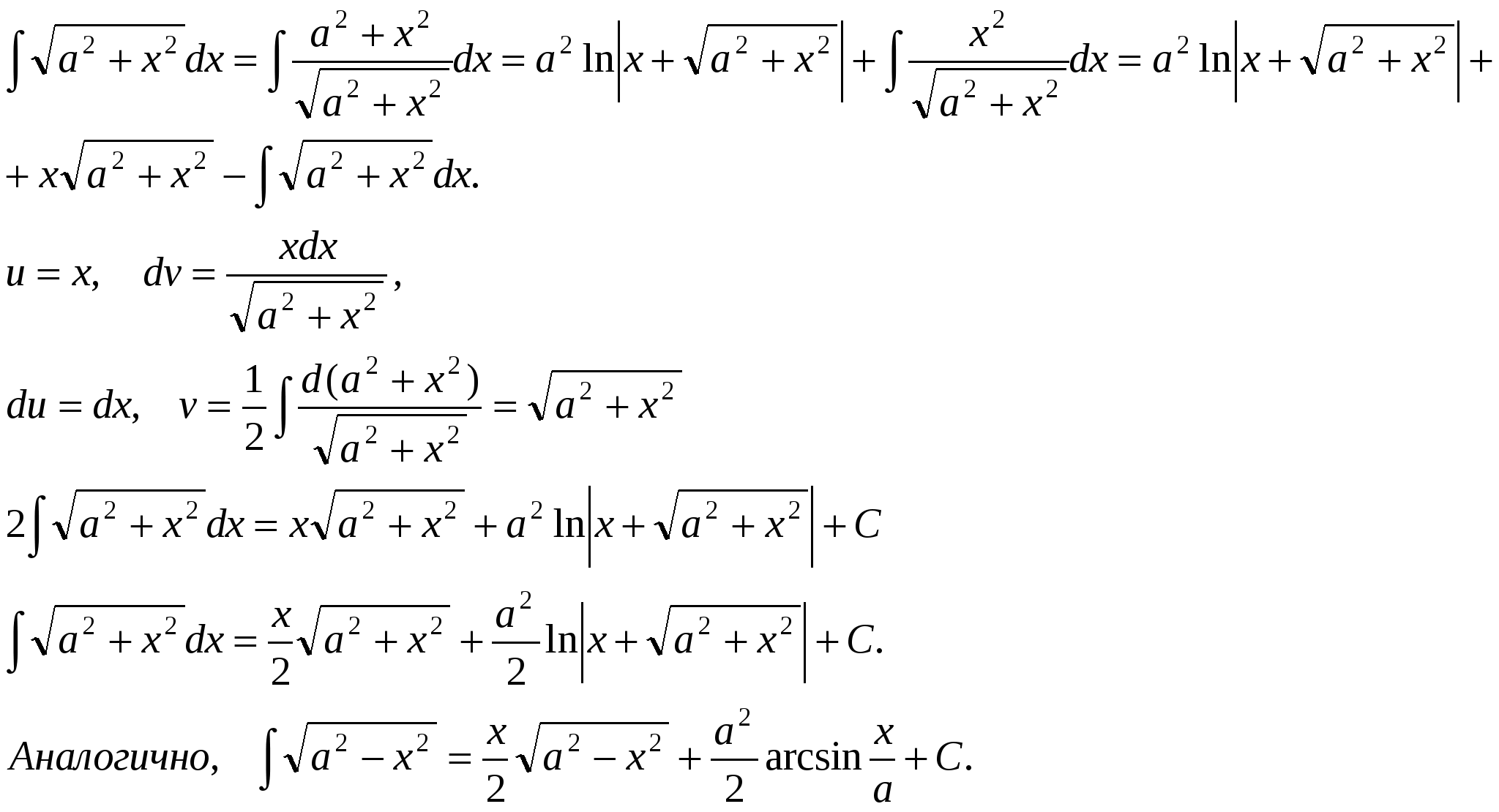 Интегралы от некоторых тригонометрических выражений. 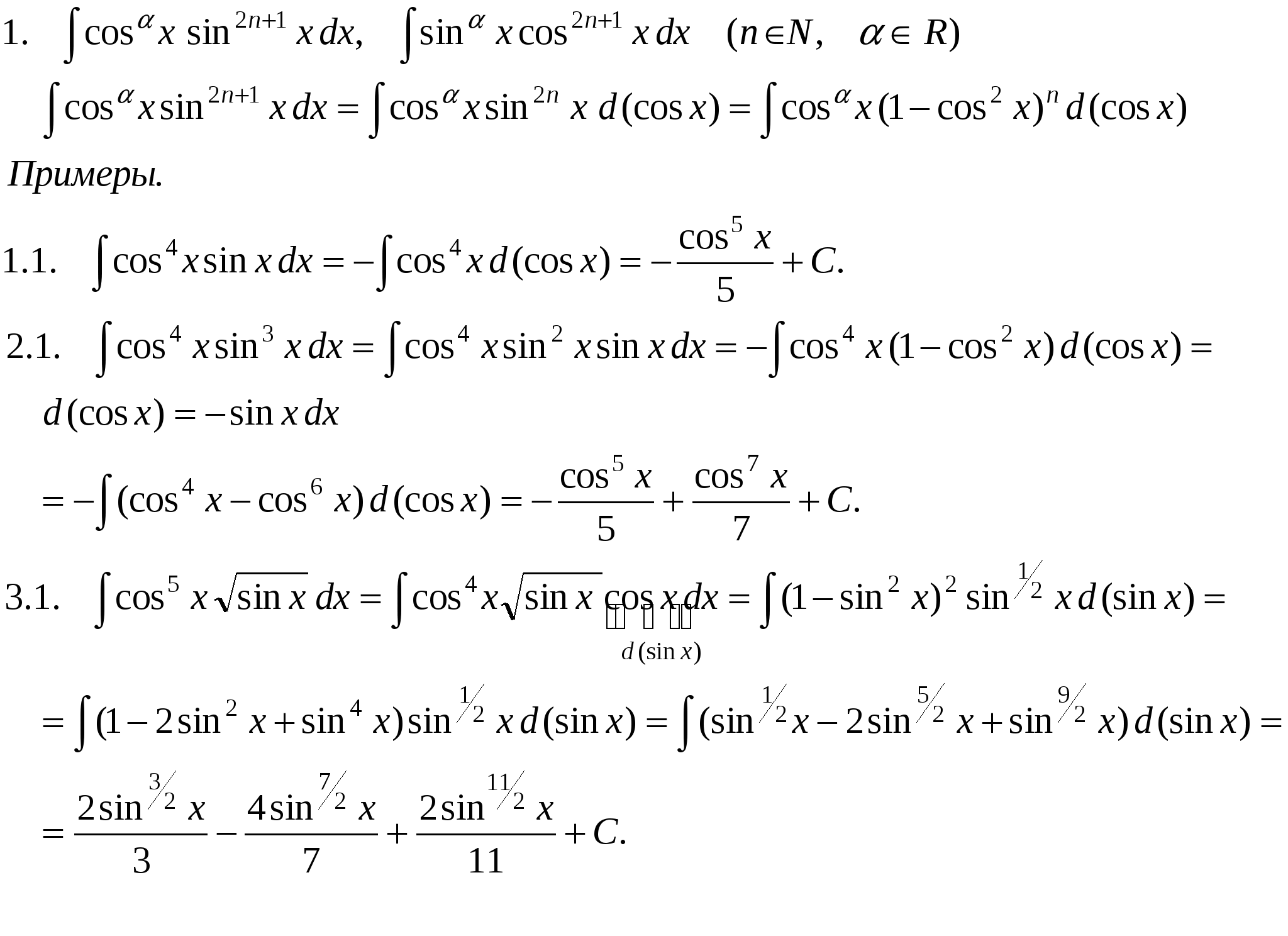 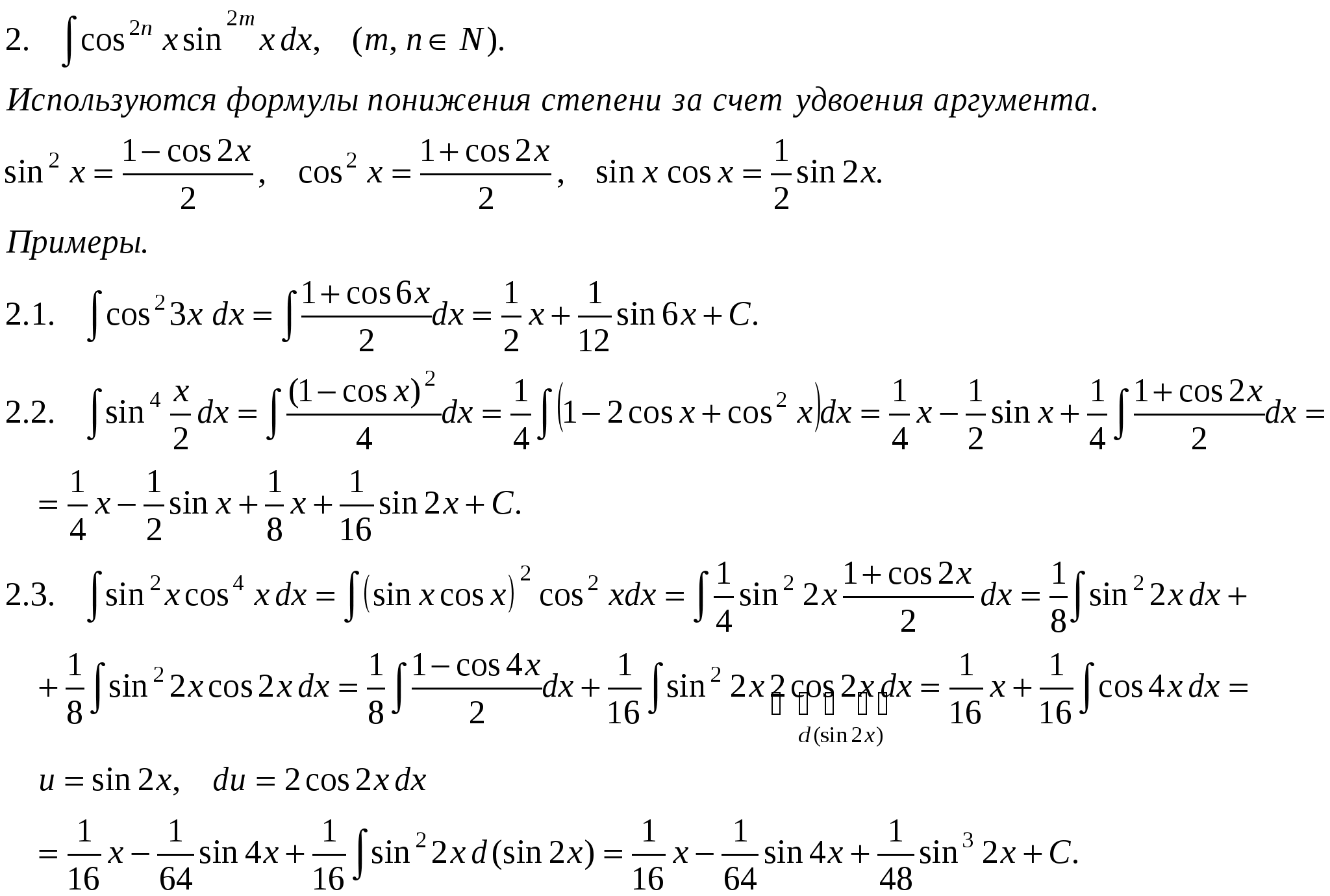 3. 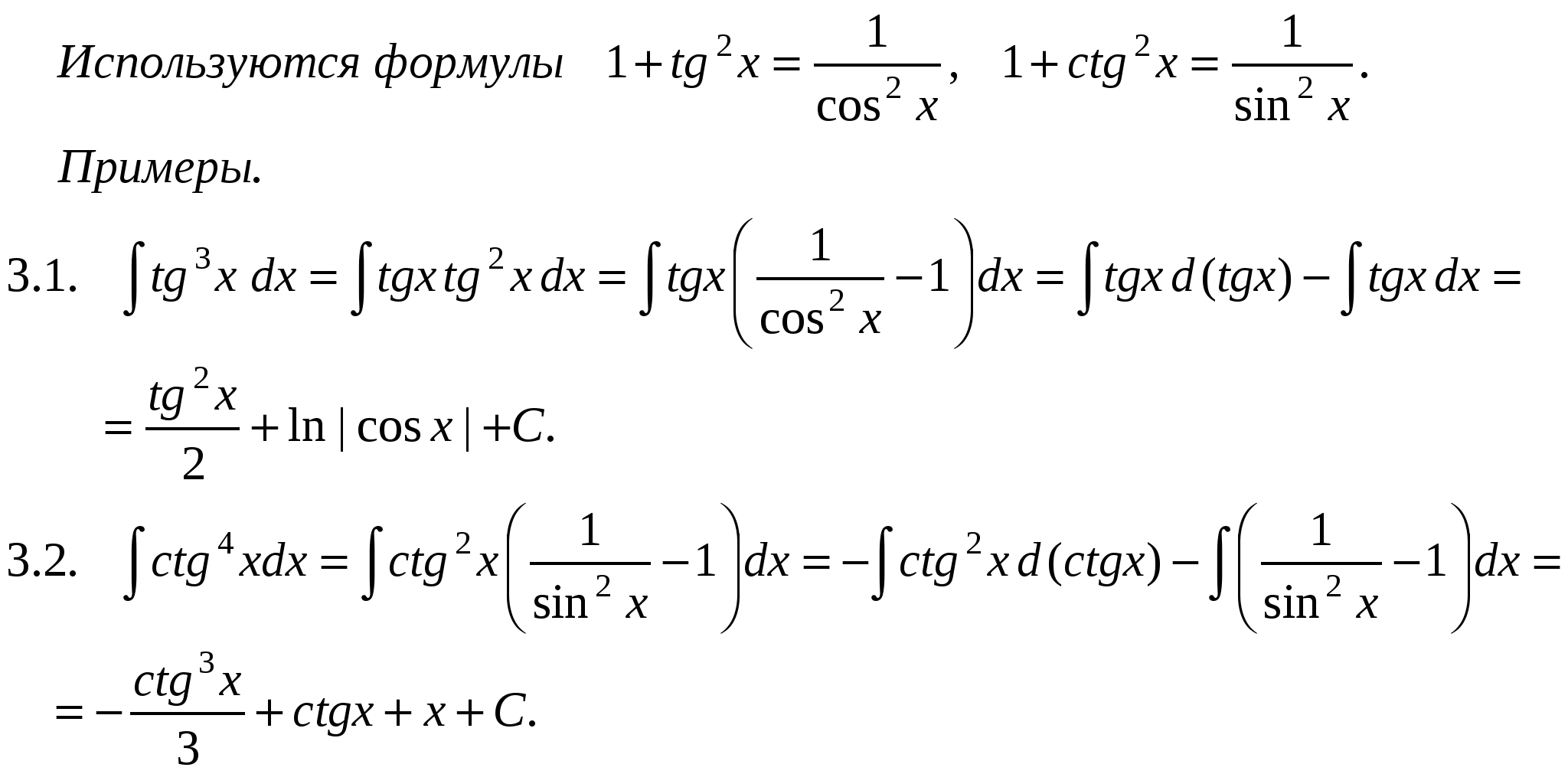 Рациональные дроби. Рациональной дробью называется дробь вида 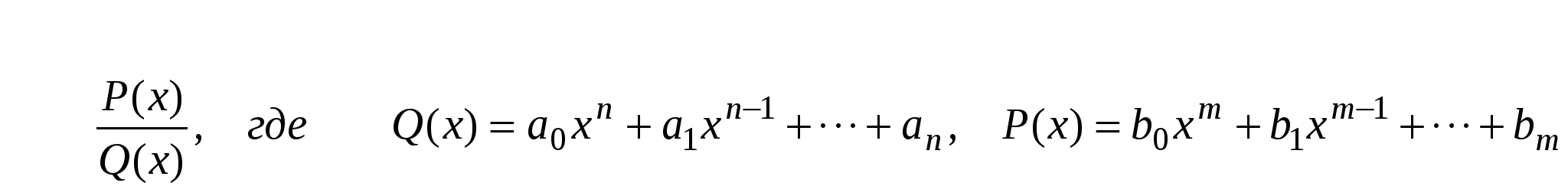 Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя (m < n). В противном случае дробь называется неправильной. 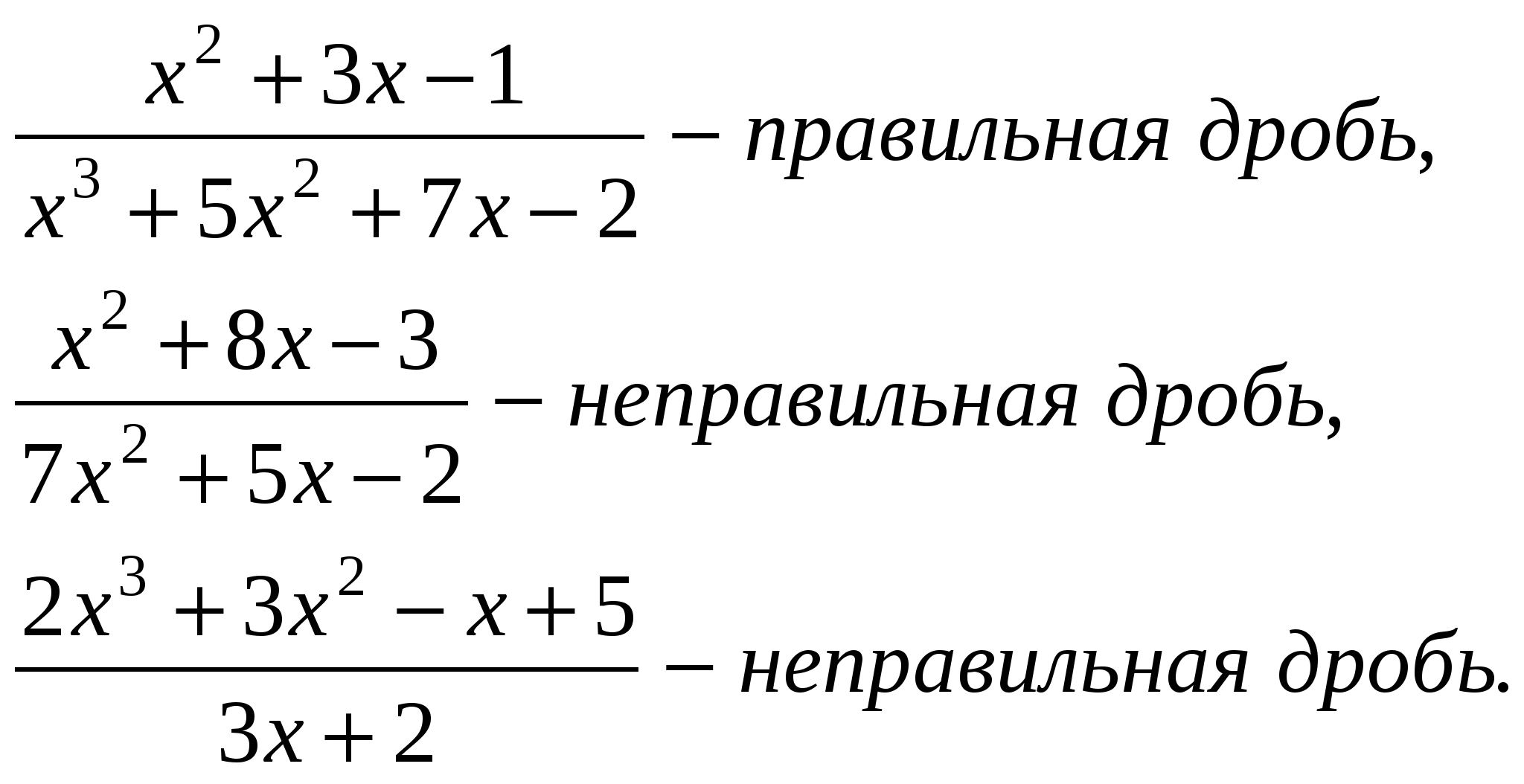 Неправильная дробь путем деления числителя на знаменатель представляется в виде суммы многочлена и правильной дроби. Эта операция называется выделением целой части. 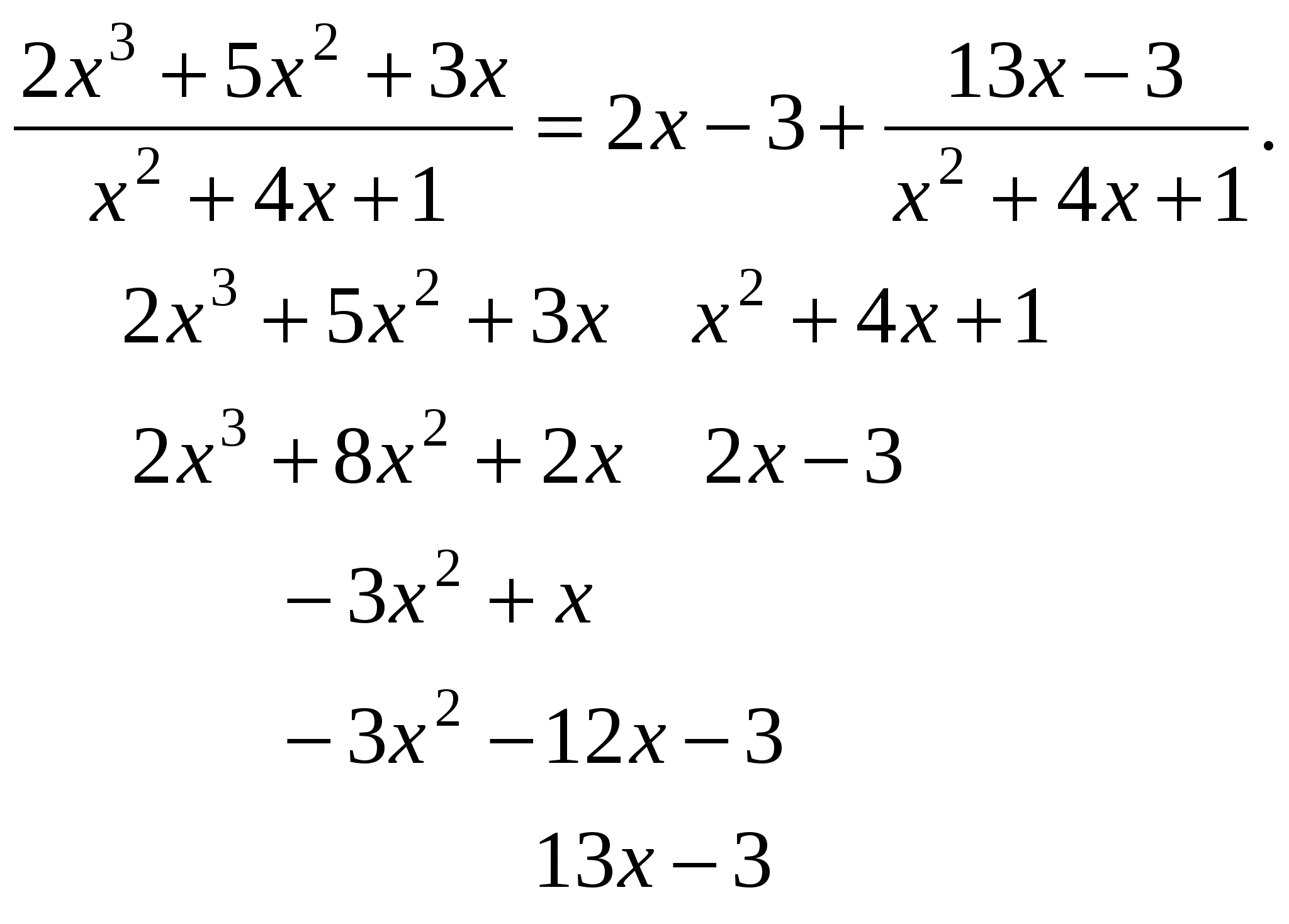       Простейшие рациональные дроби. 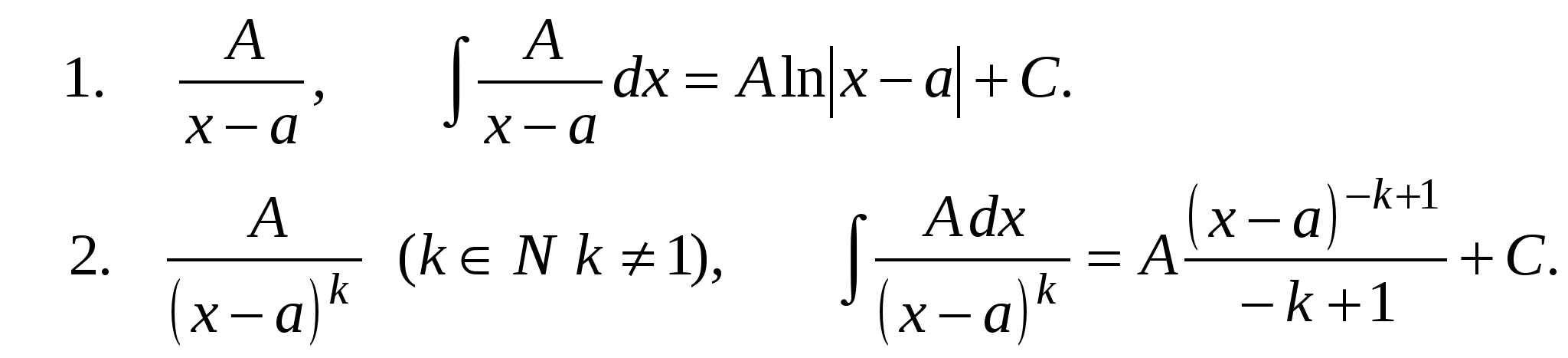 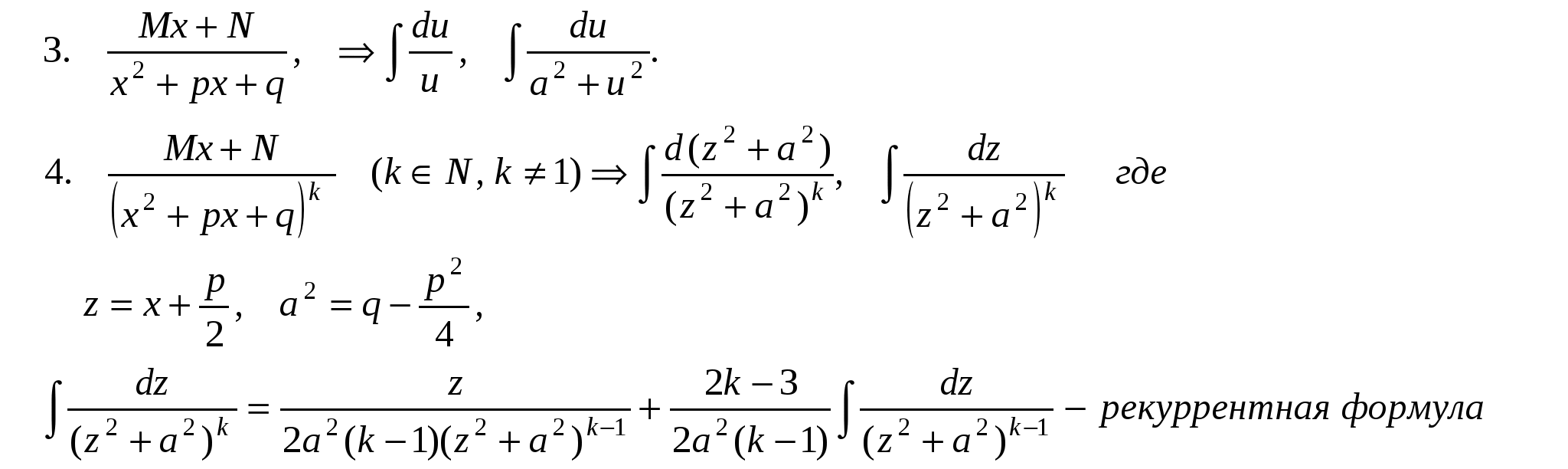 Некоторые сведения из алгебры. Q(x) = a0 xn + a1xn-1 + ... + an-1 x + an (1)
Н а п р и м е р Q(x) = x3 + 2x2 + 2x.  Q(x) = x ( x2 + 2x + 2), x1 = 0, x2,3 = -1 ± √ 1 – 2 = -1 ± i Q(x) = x ( x2 + 2x + 2), x1 = 0, x2,3 = -1 ± √ 1 – 2 = -1 ± i
Q(x) = a0(x – x1) (x – x2) .... (x – xn) (2)
(x – α - β i) (x – α + β i) = (x – α)2 – β2 i2 = x2 – 2 α x + α2 + β 2 = x2 + px + q, где p = -2 α, q = α2 + β2 – квадратный трехчлен, не разлагающийся на действительные множители.
(x − α − β i)l (x − α + β i)l = ( x2 – px + q)l На основании этого многочлен (1) запишется в виде (3) – разложение многочлена (1) на простейшие действительные множители, к1 + k2 +… + kr + 2l1 + 2l2 + … + 2ls = n П р и м е р. x5 – 2x3 – 8x = x(x2 + 2) (x2 – 4) = x(x2 +2) (x – 2) (x + 2). Теорема о разложении правильной рациональной дроби на простейшие. 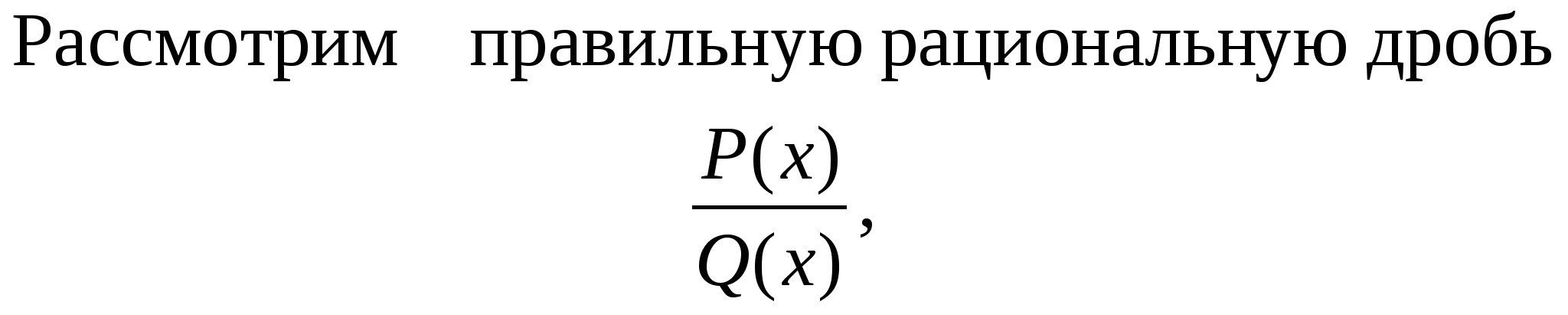 где Q(x) представляется в виде (3). Данная дробь представляется как сумма простейших следующим образом 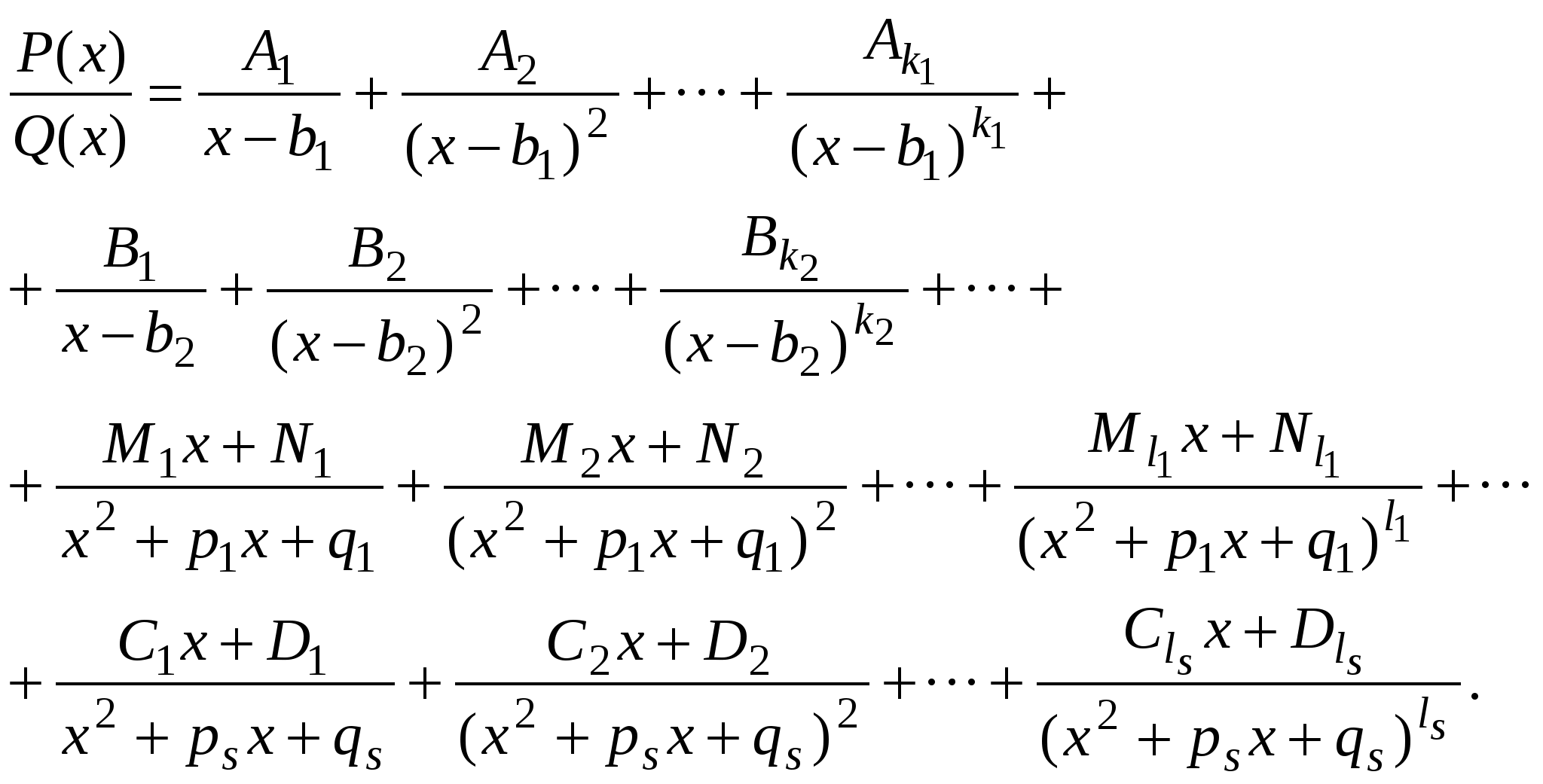 Интегрирование рациональных дробей. При интегрировании рациональных дробей следует придерживаться такого порядка.
Q(x) = a0 (x – a) (x - b)…(x – c)k …(x2 + px +q)….(x2 + p1 x +q1 )l….., где x2 + px + q – квадратный трехчлен, не разлагающийся на действительные множители.
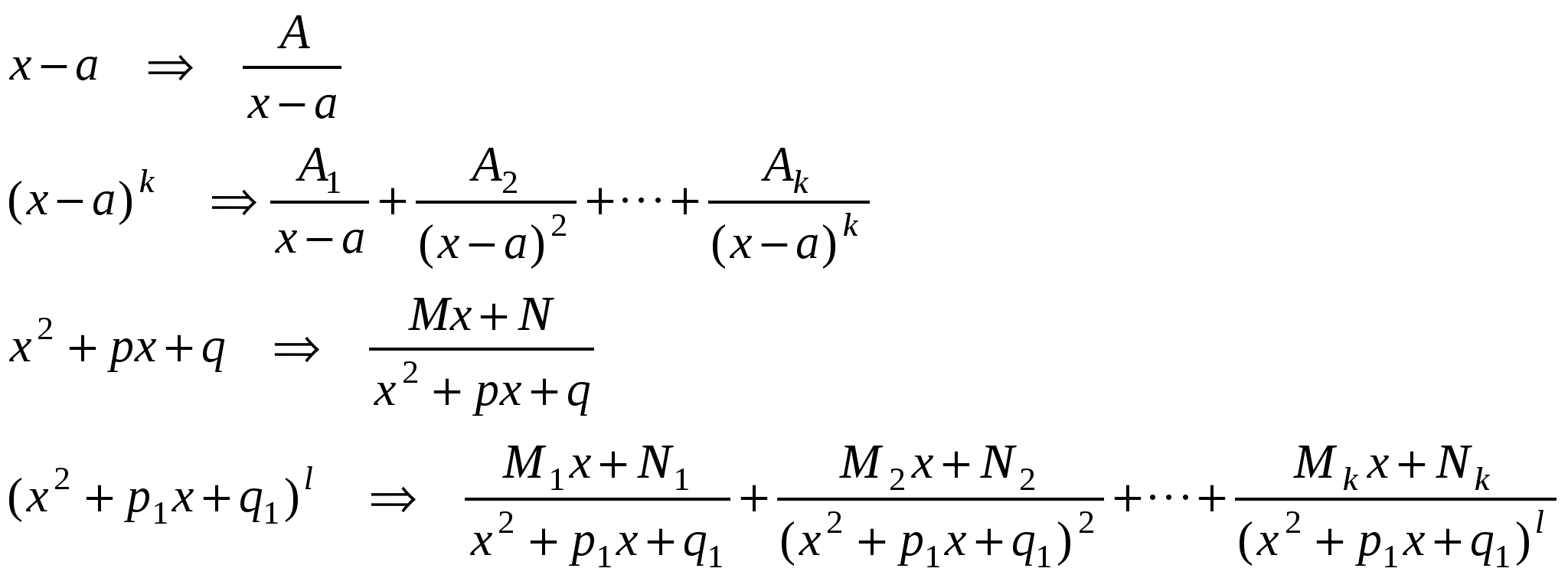
П р и м е р ы . 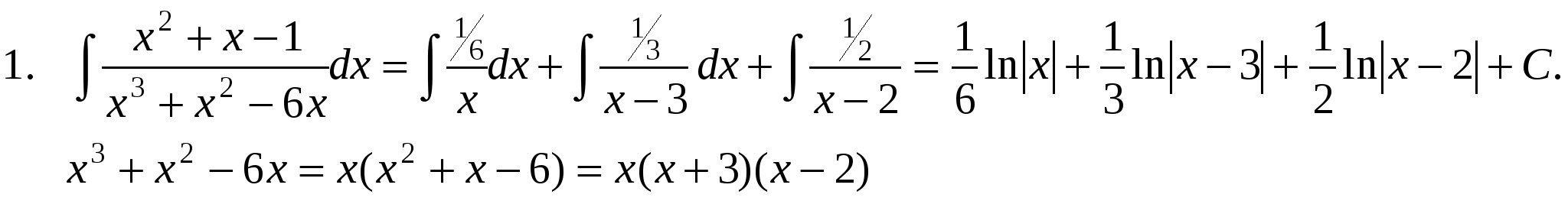 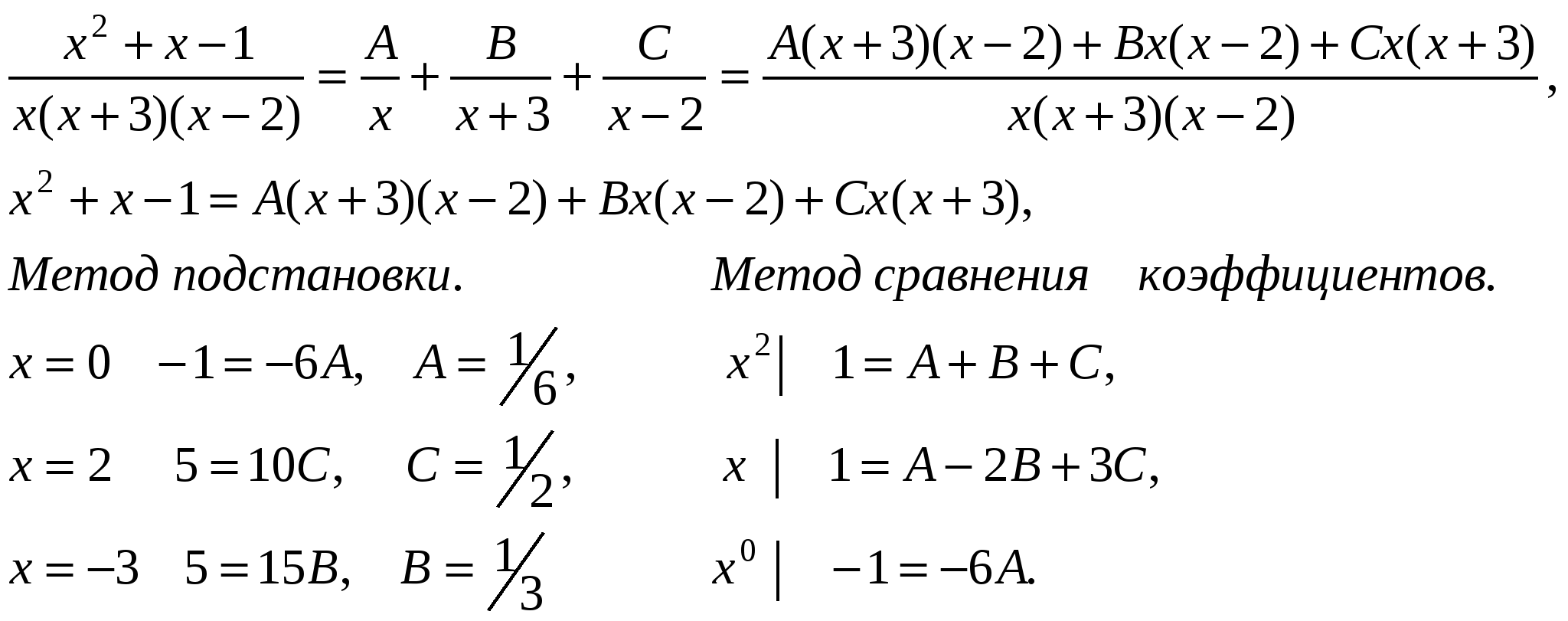 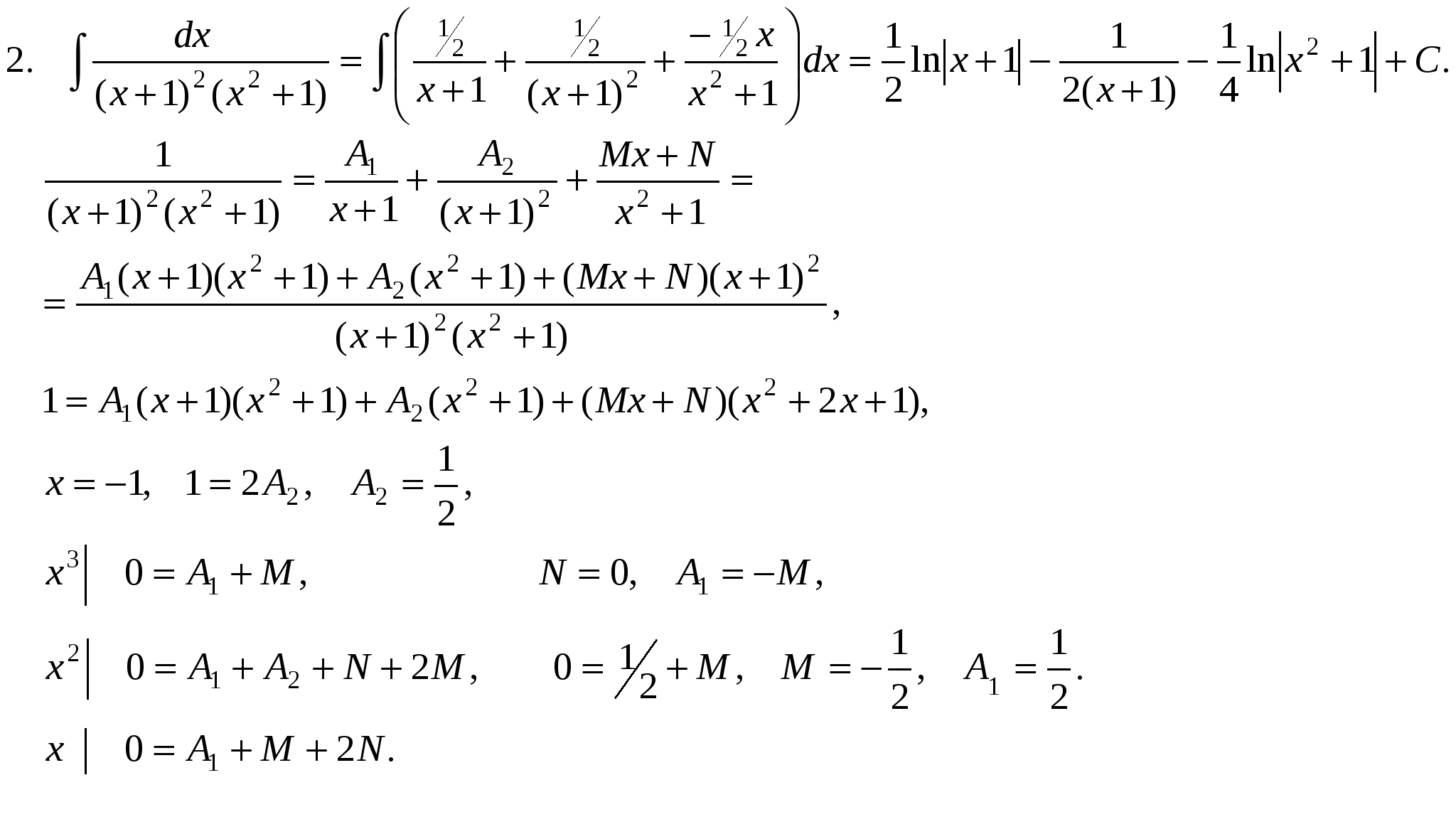 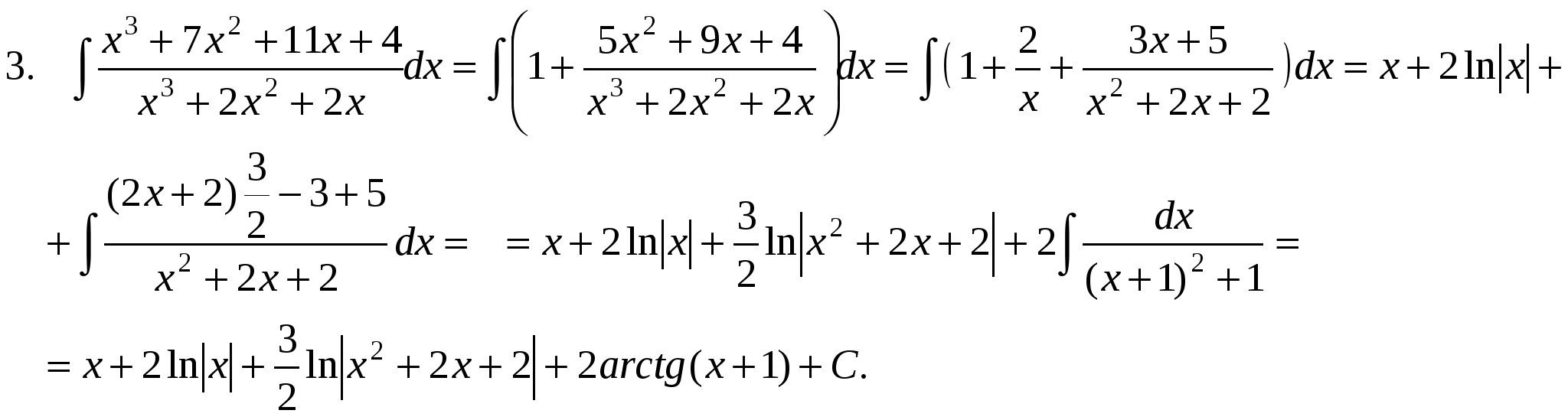   x3 + 7x2 + 11x + 4 x3 + 2x2 + 2x x3 + 7x2 + 11x + 4 x3 + 2x2 + 2x  x3 + 2x2 + 2x 1 x3 + 2x2 + 2x 15x2 + 9x + 4 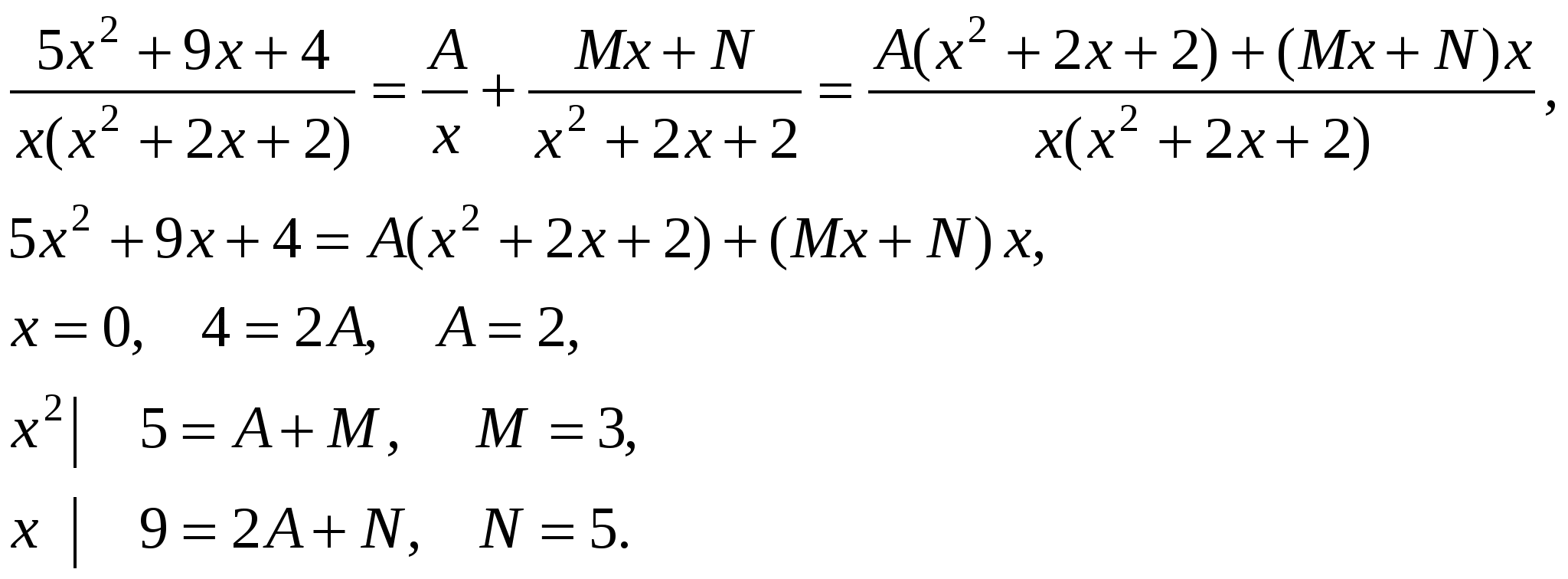 Интегралы от рациональных функций всегда и при том стандартным образом выражаются через элементарные функции. Метод рационализации – это такой метод, когда с помощью подстановки данный интеграл приводится к интегралу от рациональной функции. Сделаем замену: ax + b = ts, s = OHЗ дробей m/n, p/q, … . Интеграл сводится к интегралу от рациональной функции, т.к. П р и м е р. 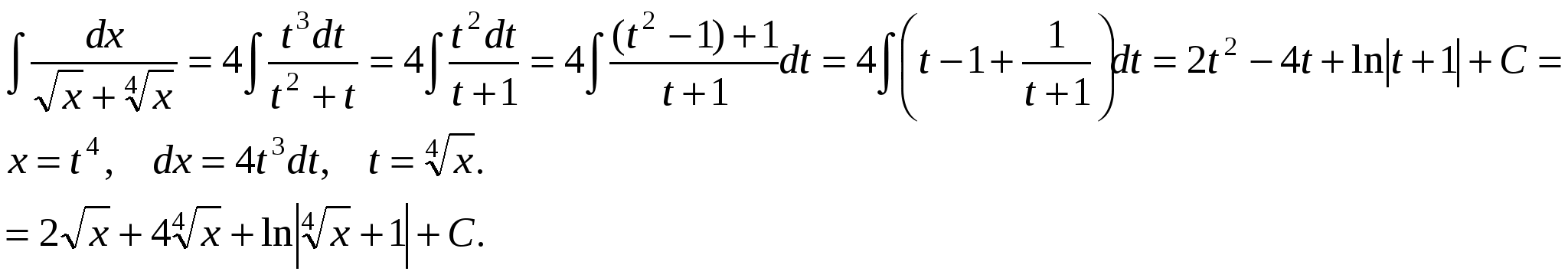
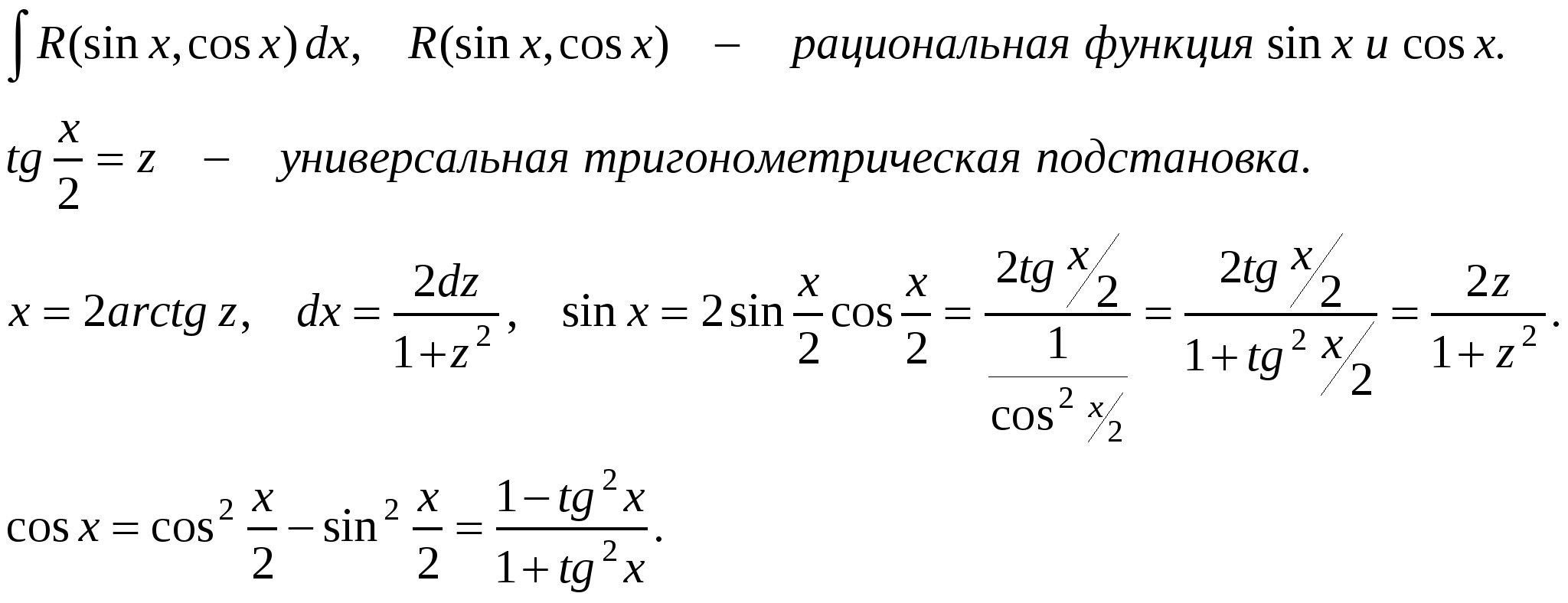 Если в данный интеграл подставить выражения для sinx, cosx и dx, то получим интеграл от рациональной функции. П р и м е р . 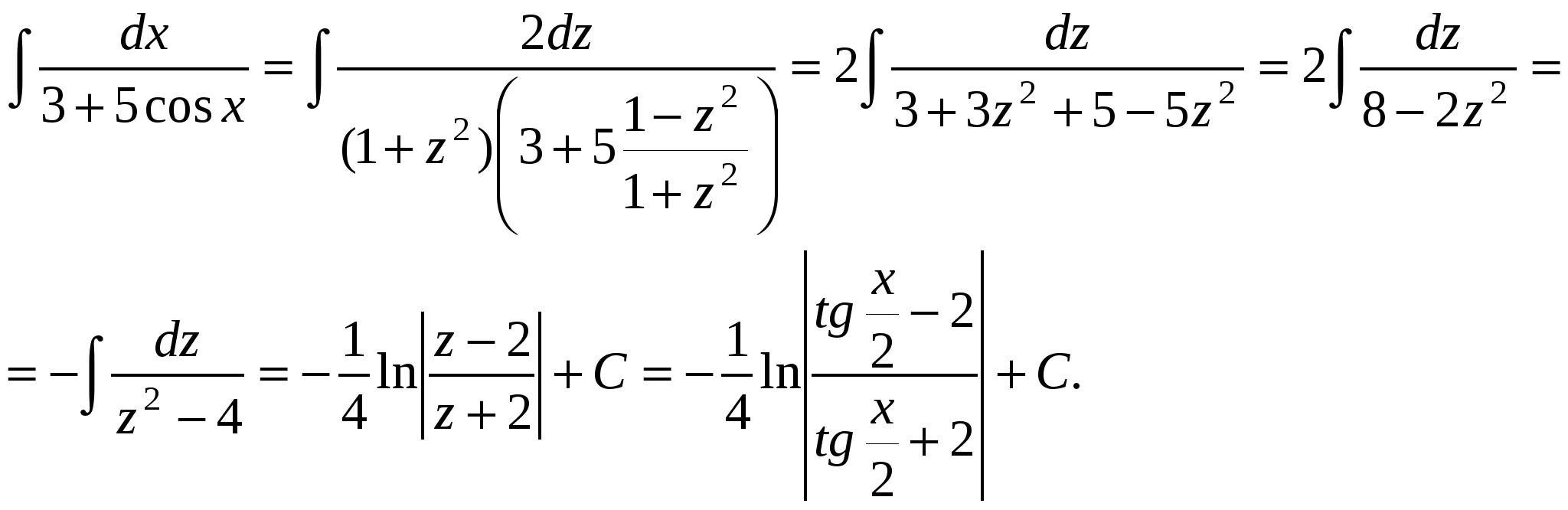 Универсальная тригонометрическая подстановка приводит в ряде случаев к сложным рациональным дробям. 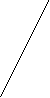   x П р и м е р. 1 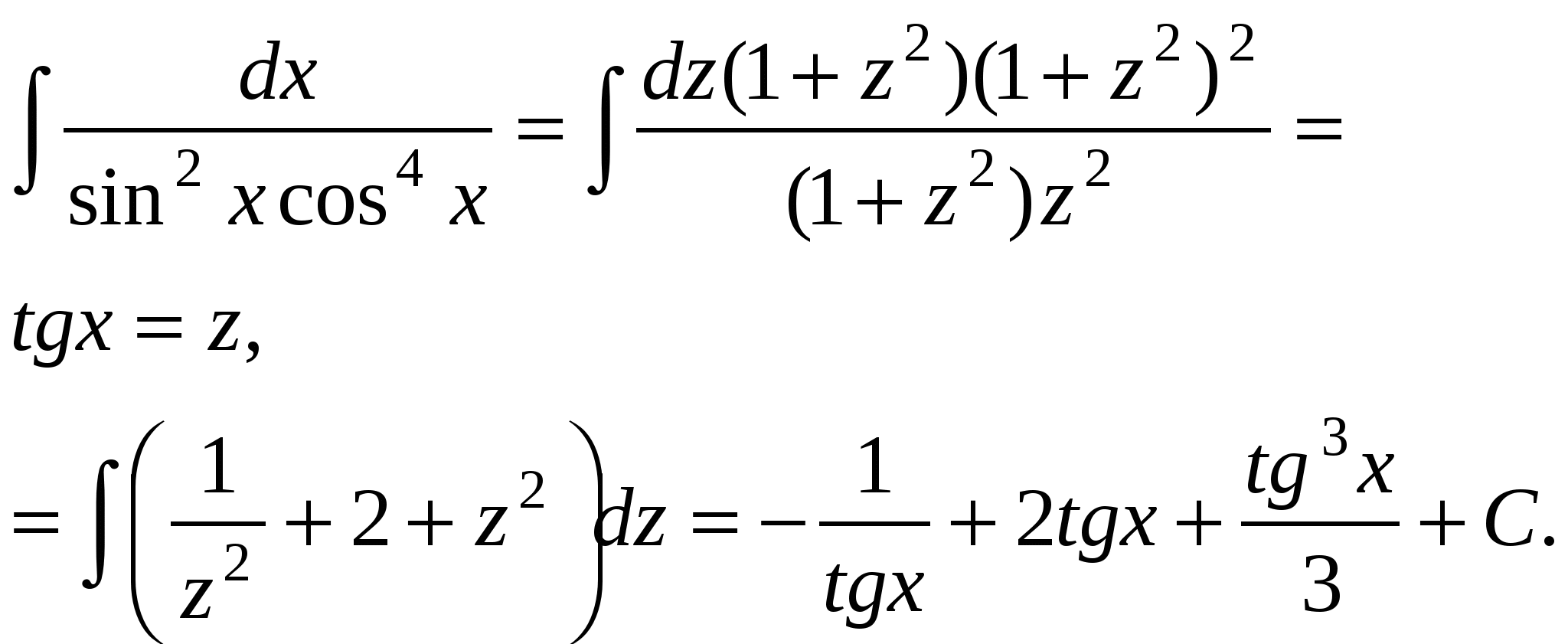
Выражение вида xm(a + bxn)p dx, где m, n и p – рациональные числа, называется дифференциальным биномом. Будем рассматривать Предположим, что m и n – целые числа, если m и n – дробные, то с помощью подстановки x = tα , где α – ОНЗ дробей m и n, интеграл (*) можно привести к такому виду, где m и n – целые. Интеграл (*) приводится к интегралу от рациональной функции в следующих трех случаях:
Чебышев доказал, что дифференциальный бином не интегрируется, если ни одно из чисел П р и м е р ы . 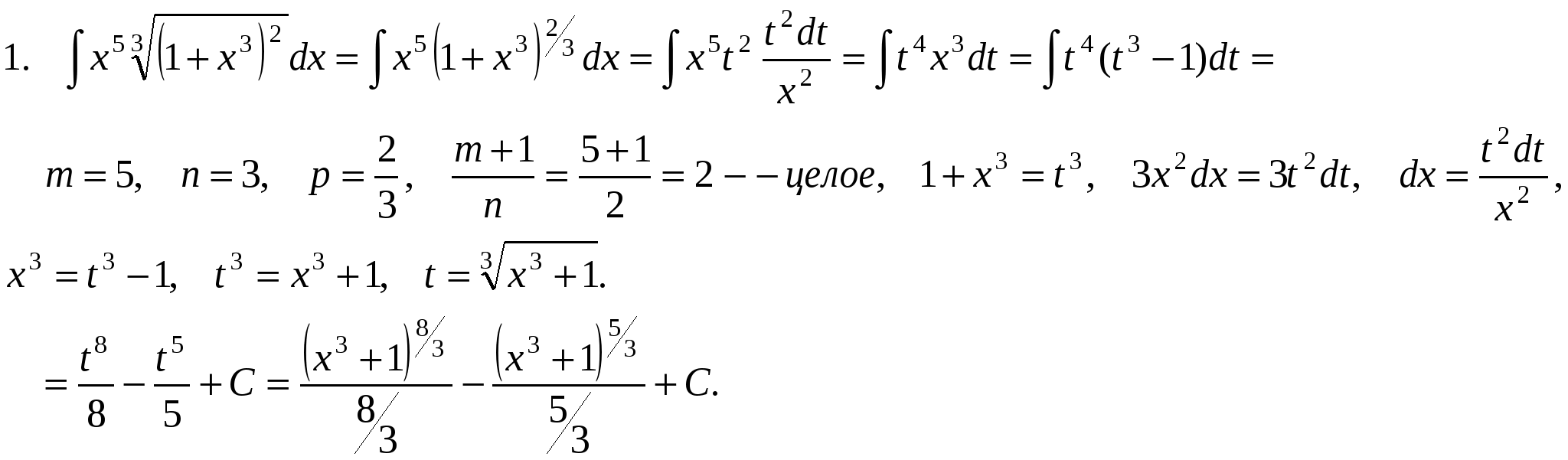 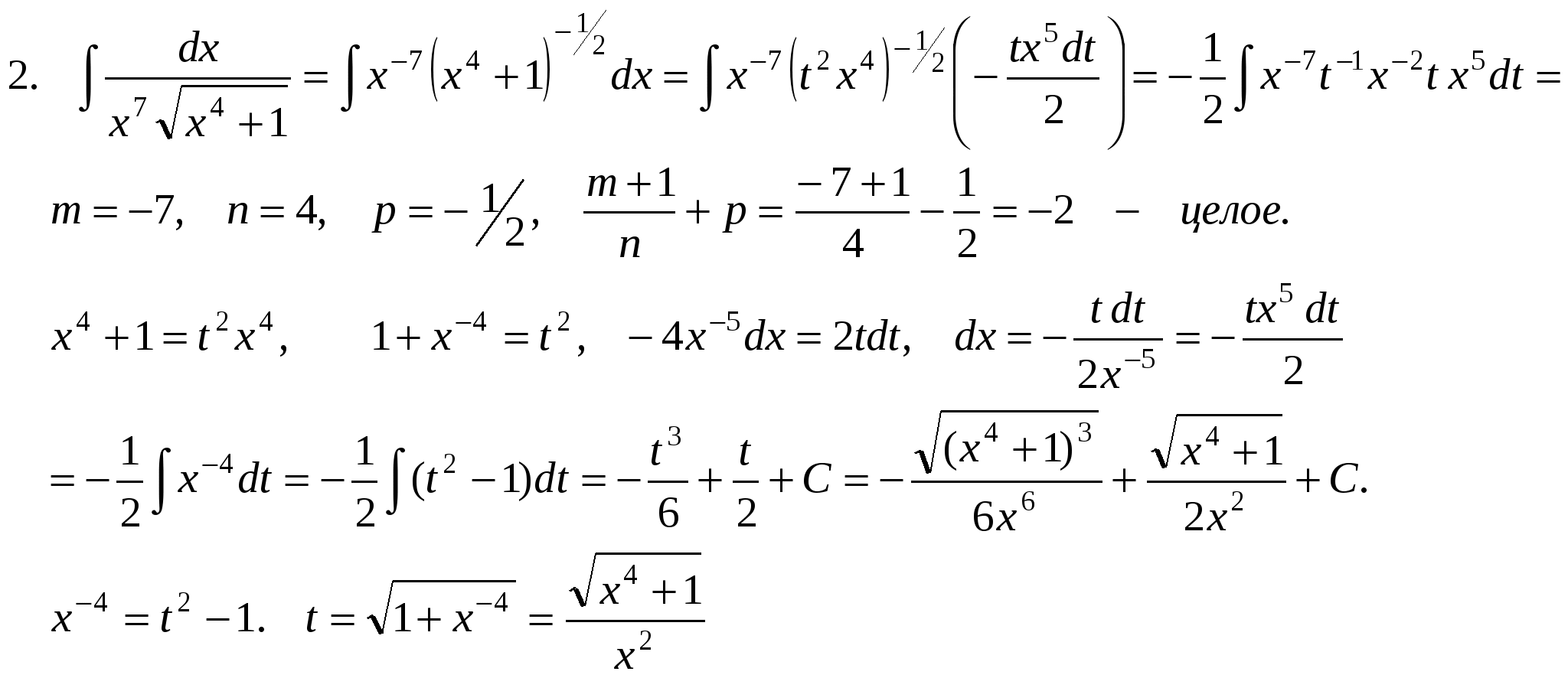 Разные задачи. 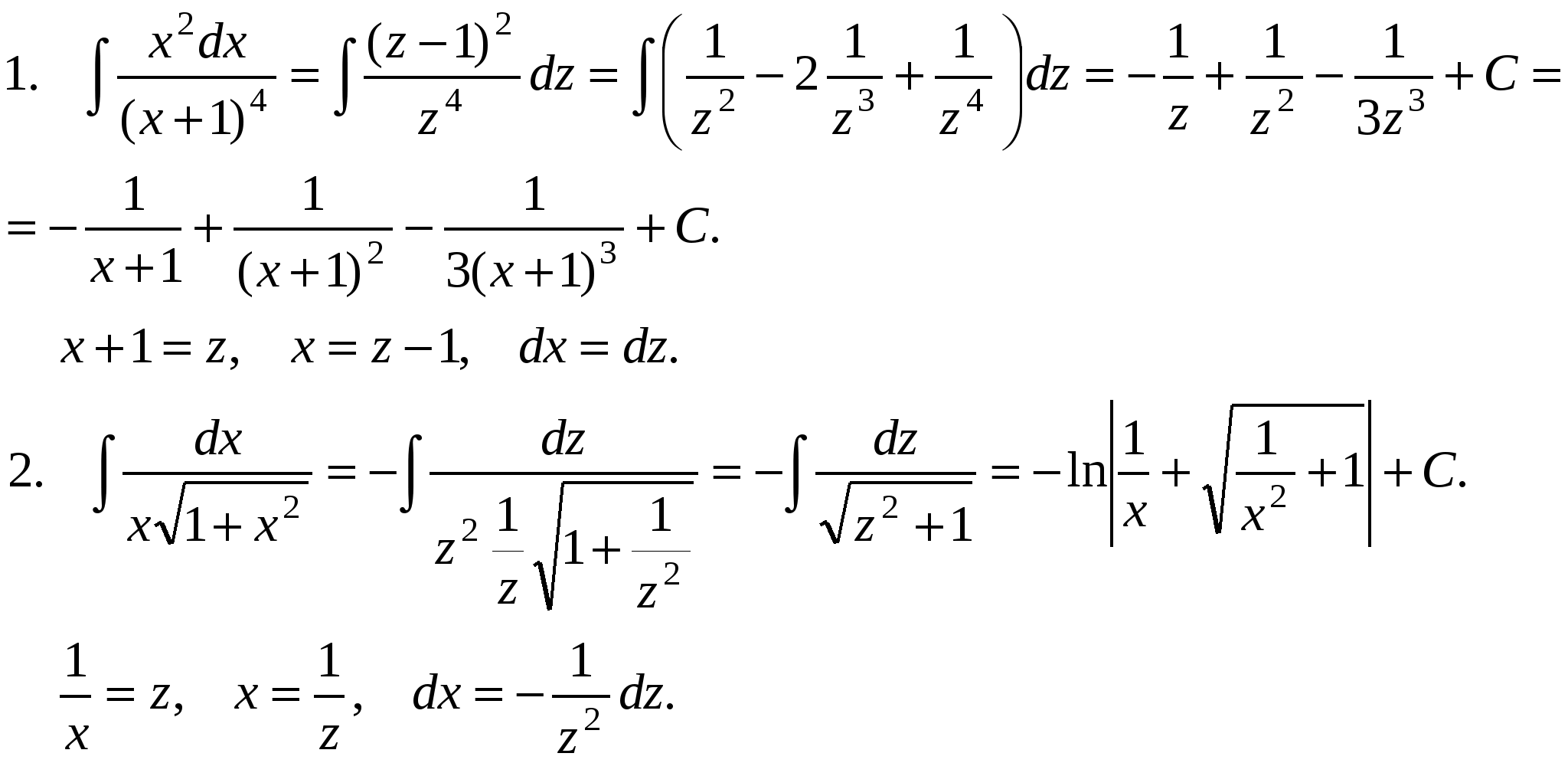 Для интегрирования используются следующие формулы тригонометрии: sin αx cos βx = ½(sin(α – β)x + sin(α + β)x) cos αx cos βx = ½(cos(α – β)x + cos(α + β)x) sin αx sin βx = ½(cos(α – β)x - cos(α + β)x) О функциях, интегралы от которых не выражаются через элементарные. Теорема существования. Если функция непрерывна, то она имеет первообразную. Однако, не всякая первообразная выражается через элементарные функции. Например,  |