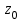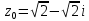КР_Мат_Ан_Вар_5. Даны функции
 Скачать 498.66 Kb. Скачать 498.66 Kb.
|
|
Задание 1 Даны функции 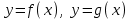 . .
Строим графики заданных функций, используя известные графики.  В качестве исходного будем рассматривать график 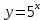 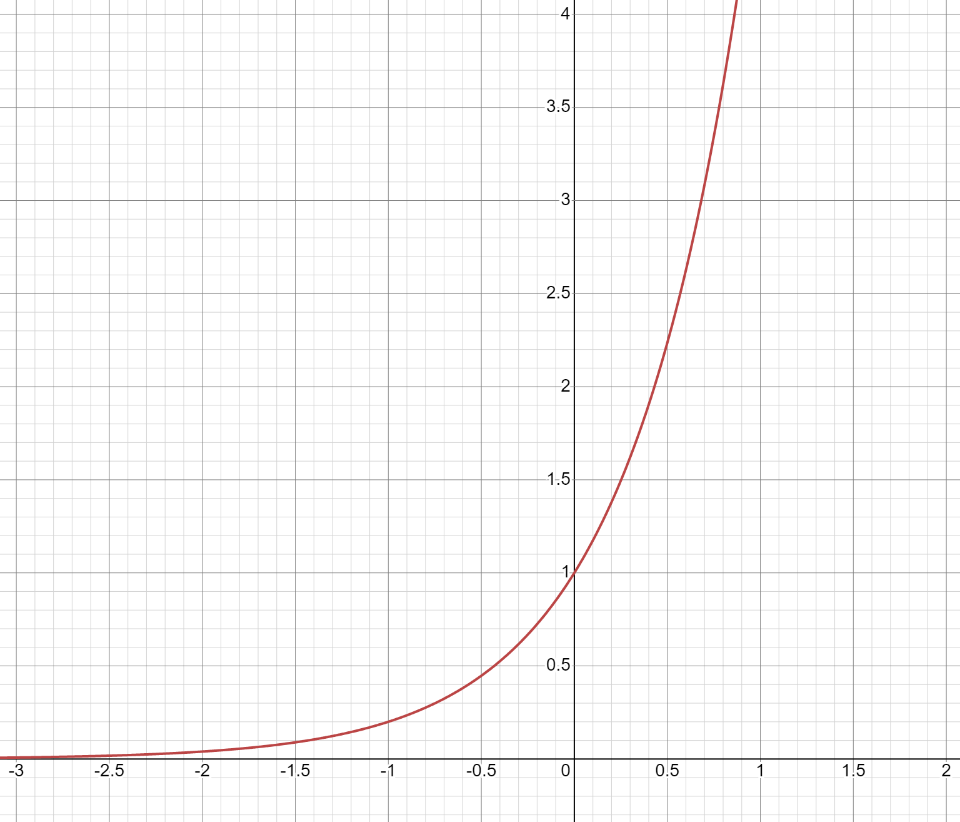  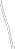 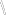  ООФ: x – любое число, y>0, y(0)=1, y(1)=5 График функции 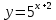 получается преобразованием графиков по формуле: получается преобразованием графиков по формуле: 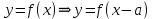 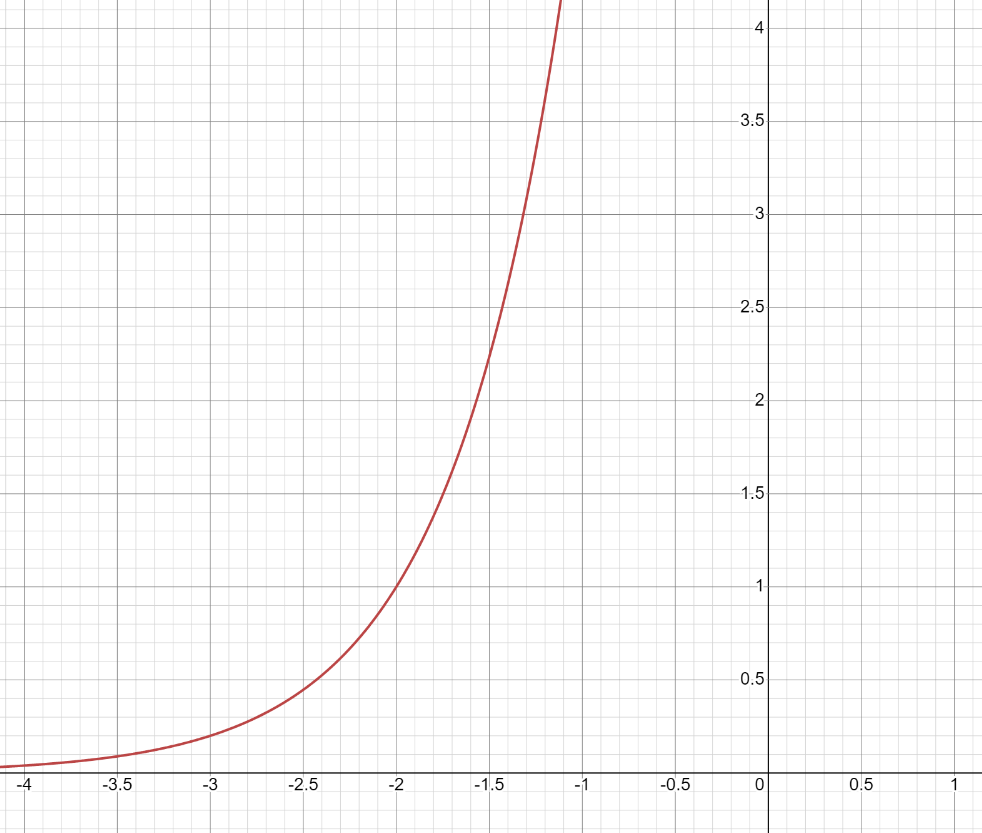 ООФ: x – любое число, y>0 График 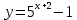 получается смещением по оси у на -1 получается смещением по оси у на -1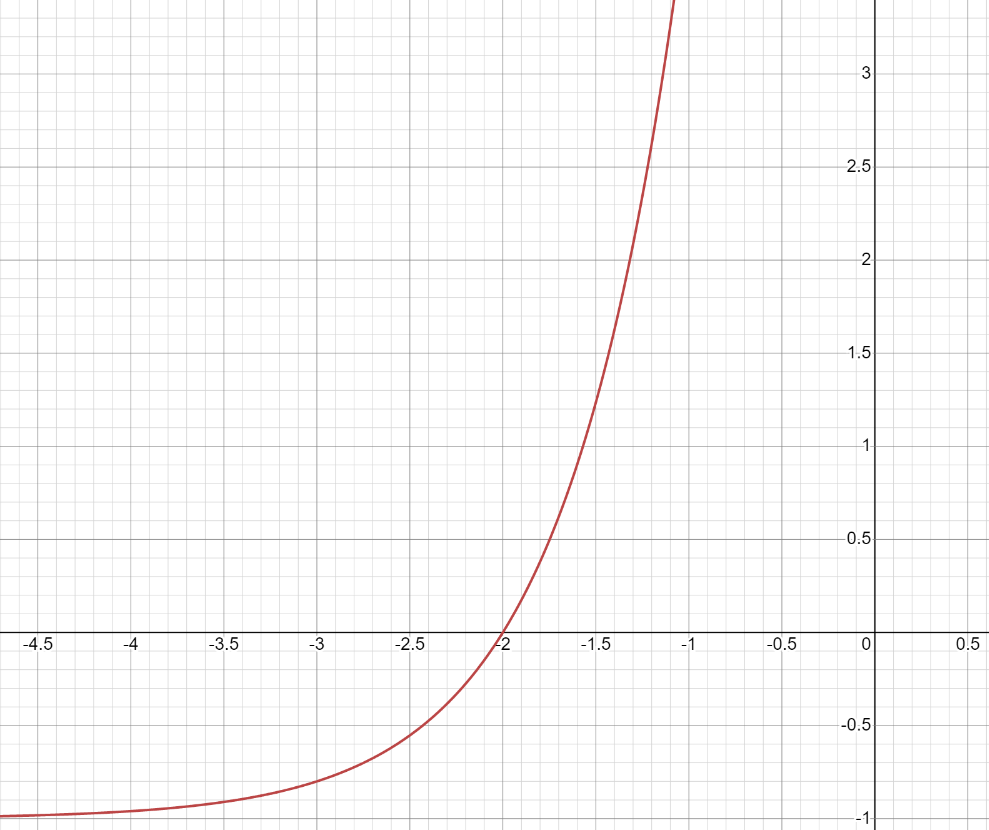 ООФ: x – любое число 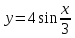 В качестве исходного будем использовать график функции 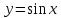 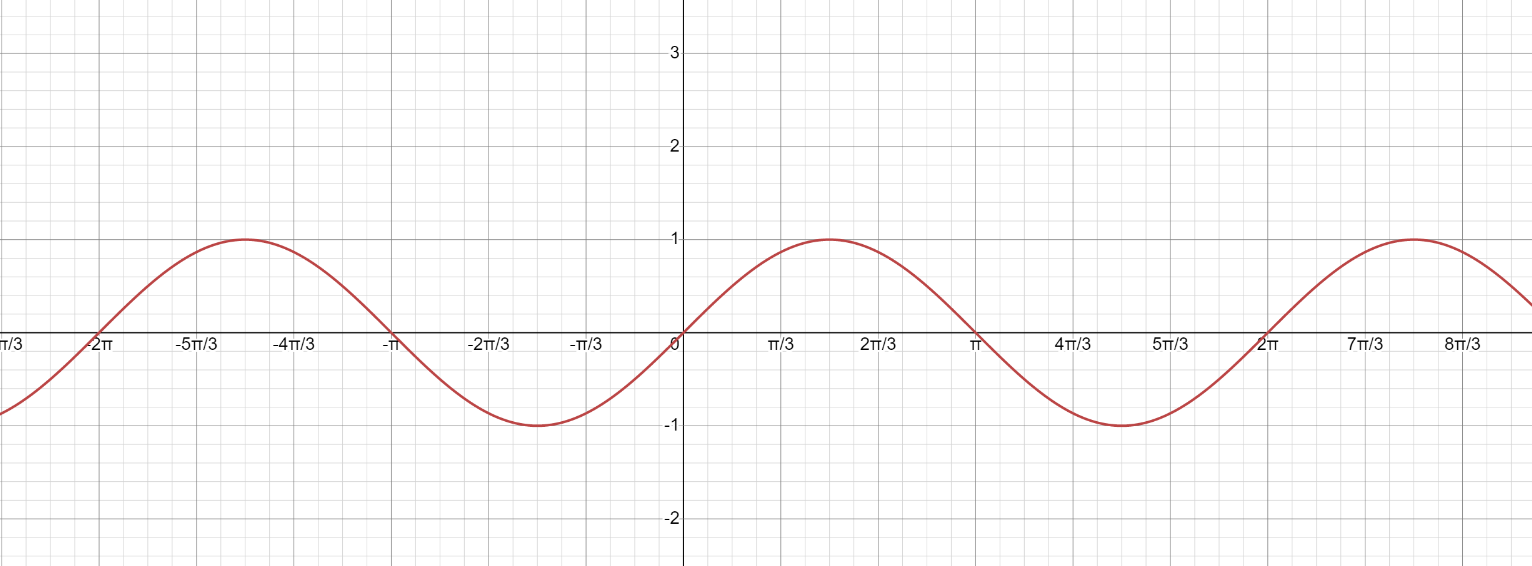 График 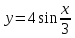 получается преобразованием в виде расширения графика в 3 раза по оси Ох, а также расширением в 4 раза по оси Оу. получается преобразованием в виде расширения графика в 3 раза по оси Ох, а также расширением в 4 раза по оси Оу.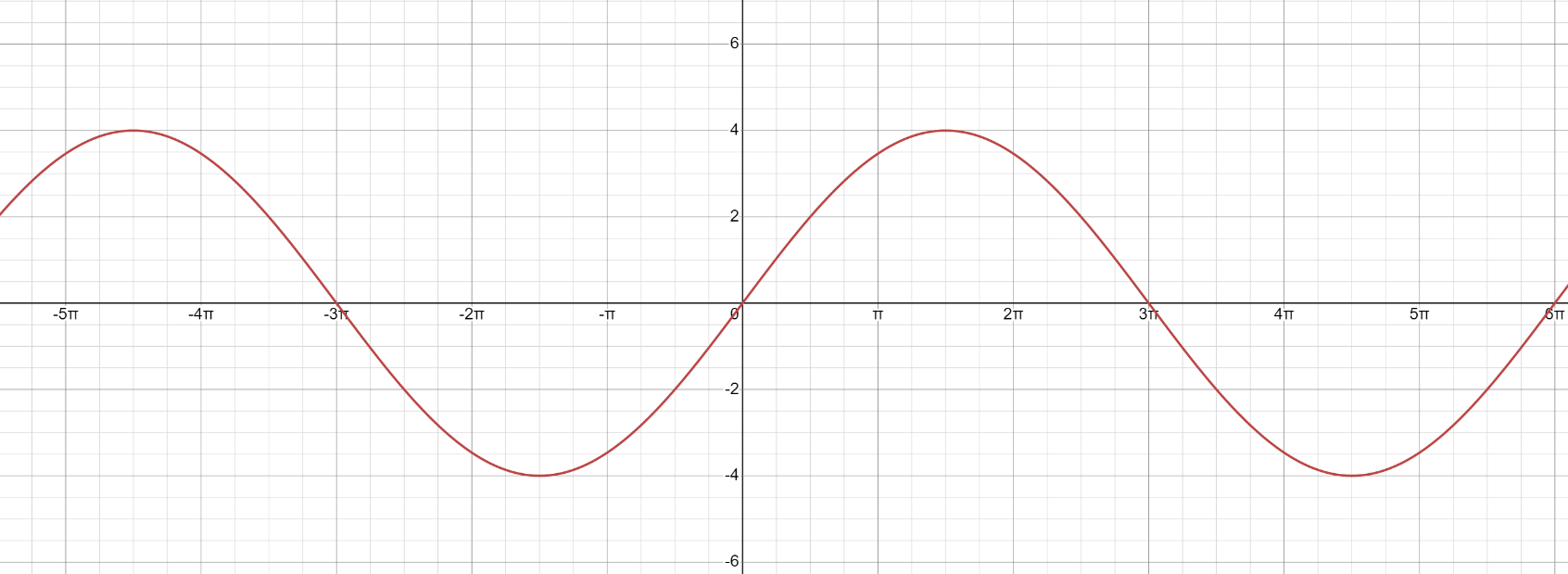
Сложные функции будут иметь вид: 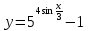 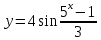 Получим и построим обратные функции: 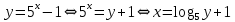 Обратная функция: 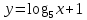 ООФ: x>0 ОЗФ: 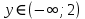 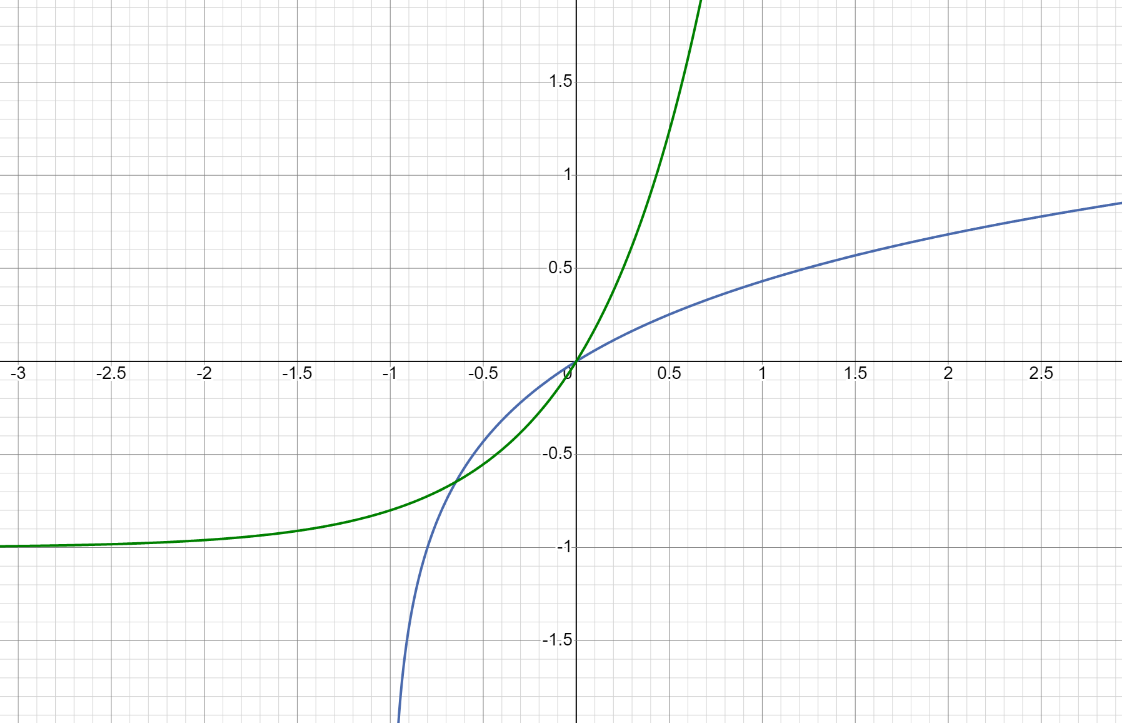 Задание 2 Вычислить пределы а) 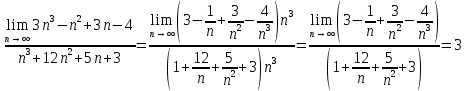 Для решения предела в числителе и знаменателе было за скобки вынесено 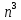 . Слагаемые, содержащие n в знаменателе будут стремится к 0. . Слагаемые, содержащие n в знаменателе будут стремится к 0. б) 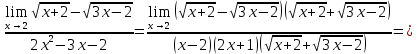 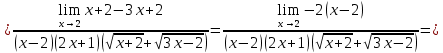 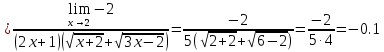 в) 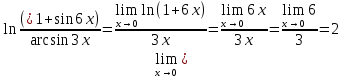 В данном примере были сделаны замены эквивалентных преобразований по табличным функциям. г) 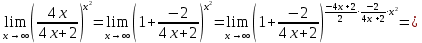 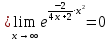 В этом пределе были сделаны преобразования для получения второго замечательного предела, переход к нему и результат получен 0, так как получена убывающая экспонента. Задание 3 а) 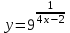 , х1 = 0, х2 = 0,5 , х1 = 0, х2 = 0,5ООФ: x≠0.5 х=0 попадает в эту область, а х=0.5 не попадает в нее, а является точкой ее разрыва. Для точки х=0 рассмотрим предел: 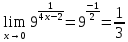 , значит, функция в этой точке непрерывна. , значит, функция в этой точке непрерывна.б) 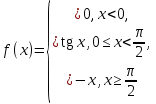 ООФ: 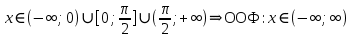 Построим кусочки функции: у = 0 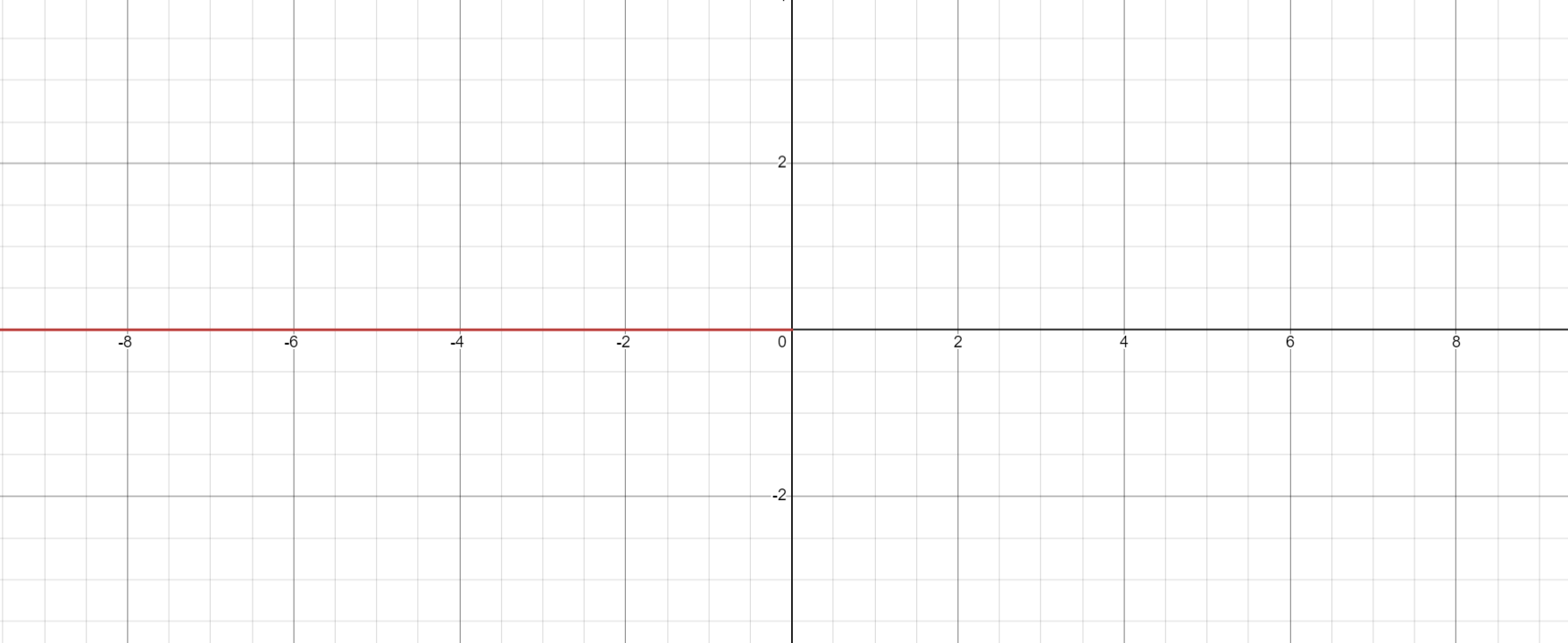 y = tg x 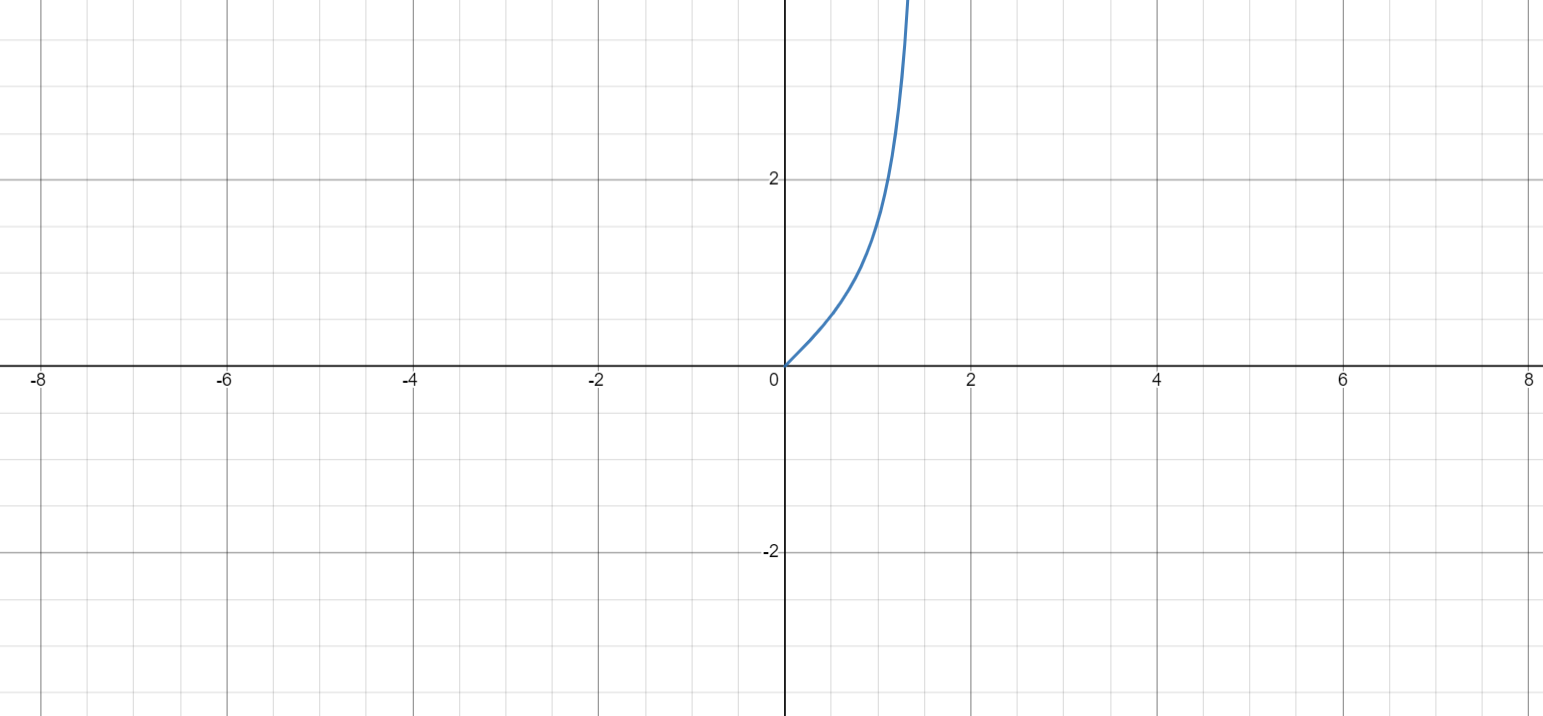 y = -x 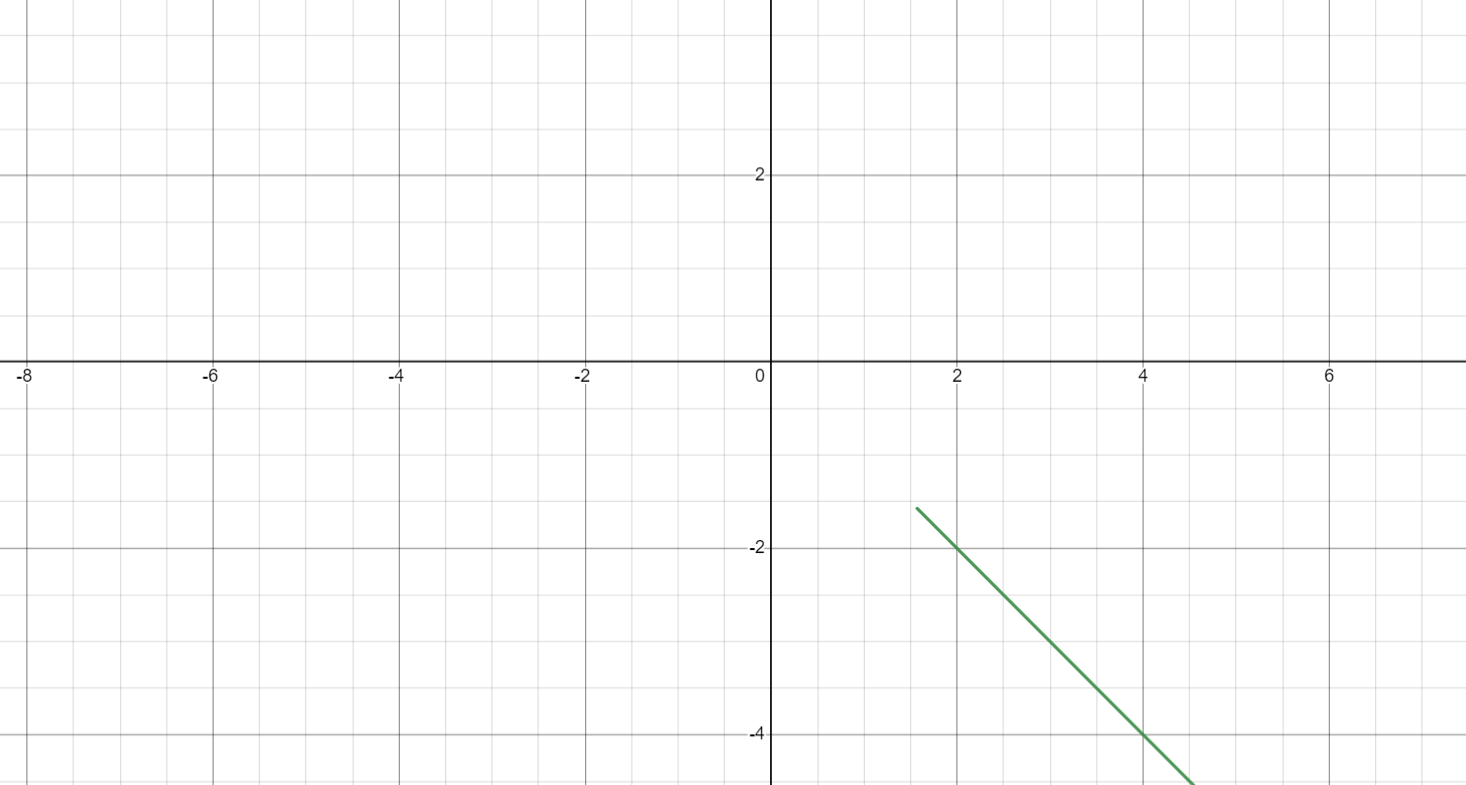 Общий вид функции: 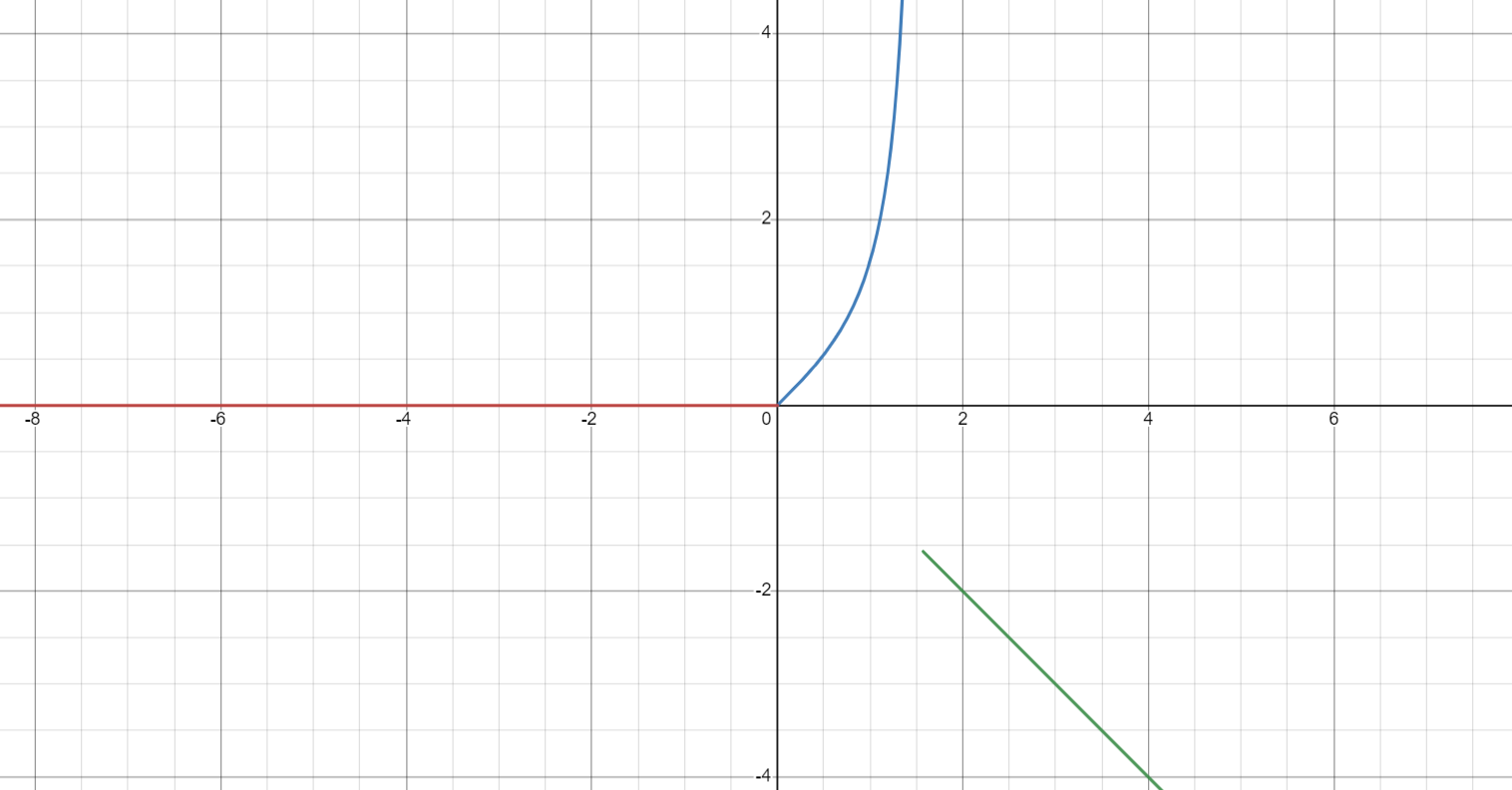 Из функции видно, что в точке ℼ/2 наблюдается разрыв. Тогда промежутки непрерывности: 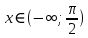 и и 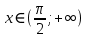 В точке х = ℼ/2 функция имеет разрыв типа «скачок», т.к. не существует 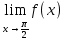 , но при , но при 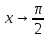 существуют конечные односторонние пределы функции, не совпадающие между собой. существуют конечные односторонние пределы функции, не совпадающие между собой.Задание 4
Найдем корни уравнения: 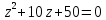 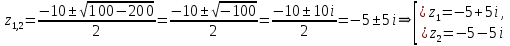 Найти комплексное число в алгебраической форме: 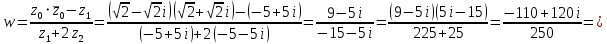 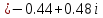 Получим тригонометрическую форму числа: Вычислим модуль комплексного числа 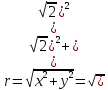 и его аргумент: и его аргумент: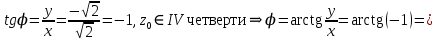 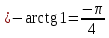 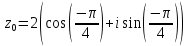 При возведении в степень, получим: 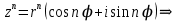 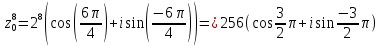 Тогда получим: 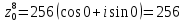 |

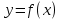
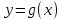
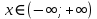
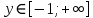
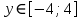
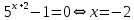
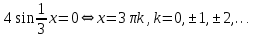
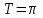
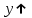 при
при 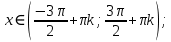
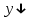 при
при 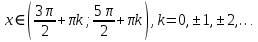
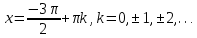 – точки min,
– точки min, 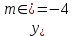
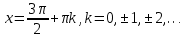 – точки max,
– точки max,