ДЗ2. Дано r 1 30 Ом
 Скачать 148.06 Kb. Скачать 148.06 Kb.
|
|
РГР 2. Вариант №76 Дано: R1=30 Ом; L2=0,56Гн; C3=57 мкФ; Em4=44В; Em6=84В; ψ4=1200; ψ6=500; f=68 Гц.         W a           C3 C3  i1 R1 i1 R1   n n      m L2 i2 i3 m L2 i2 i3    e4 e6 e4 e6    b Рис.1 Предварительные расчёты Прежде, чем приступать к выполнению поставленных задач, выполним некоторые подготовительные действия: Вычисление комплексов э.д.с. ветвей По условию для каждой э.д.с. заданы амплитуда Em и начальная фаза ψ. Для каждой э.д.с. вычислим её действующее значение E, действительную ReE и мнимую ImE части и запишем комплексы э.д.с.: E = ReE + jImE = Eejψ ; E= Em /√2; ReE = E cos ψ; ImE = E sin ψ ; Для наших данных получим: 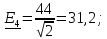 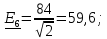 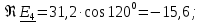 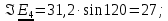 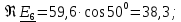 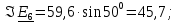 Вычисление полных комплексных сопротивлений ветвей Полное комплексное сопротивление ветви определяется по формуле: 𝑍 = 𝑅 + 𝑗𝑋 = 𝑅 + (𝑋L − 𝑋𝐶) где R – активное сопротивление ветви; X = XL − XC – реактивное сопротивление; X𝐿 = ωL – реактивное индуктивное сопротивление; X𝐶 = 1/𝜔𝐶 – реактивное ёмкостное сопротивление; ω = 2πf – угловая частота. Подставив числовые значения, получим: 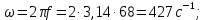 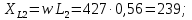 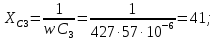 Комплексные сопротивления ветвей 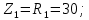 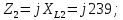 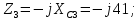 Все сопротивления в Омах. 1. По законам Кирхгофа составим систему уравнений для расчёта токов во всех ветвях, записав её в двух формах: для мгновенных значений (дифференциальная форма): Связь между токами и напряжениями на отдельных элементах для мгновенных значений имеет вид: для активного сопротивления: u = R ∙ i для индуктивности: u = L ∙ di/ dt для ёмкости: u = (1/ C) ∙ ∫ i dt Отметим для удобства три дополнительные точки: m, n, k ( рис. 1), не являющиеся узлами. Данная цепь (рис. 1) имеет 3 ветви и 2 узла (a и b). Поэтому необходимо составить систему трёх уравнений с тремя неизвестными. Одно уравнение составим по 1-му закону Кирхгофа, два – по второму: уравнение для узла a: i1 + i2 + i3 = 0; уравнение для левого контура abma: 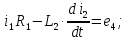 уравнение для правого контура anba: 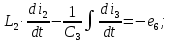 Таким образом, получаем систему 3 интегро-дифференциальных уравнений с 3 неизвестными токами i1 , i2 , i3 : i1 + i2 + i3 = 0; 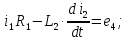 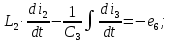 для комплексов (символическая форма): Связь между комплексами токов и напряжений на отдельных элементах имеет вид: для активного сопротивления: U = R ∙ I для индуктивности: U = jωL ∙ I = jxL∙ I для ёмкости: U = (1/ jωC) ∙I = −jxC∙I; уравнение для узла a: 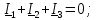 уравнение для левого контура amba: 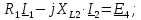 уравнение для правого контура anba: 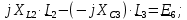 Получаем систему 3 уравнений с 3 неизвестными токами: 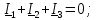 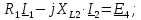 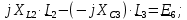 2. Определить комплексы токов в ветвях методом двух узлов Поскольку данная цепь (рис. 1) имеет 2 узла (a и b), для её расчёта вос- пользуемся методом двух узлов. В общем случае уравнение для комплекса междуузлового напряжения имеет вид: 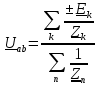 где в числителе стоит сумма по всем активным ветвям, а в знаменателе – по всем ветвям. Знак «+» в числителе выбирается, если э.д.с. направлена против междуузлового напряжения Uab . Для рассматриваемой цепи (рис. 1) получим: 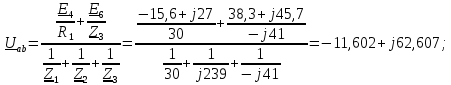 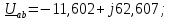 Токи в ветвях найдём по закону Ома для активной ветви: 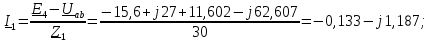 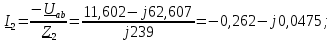 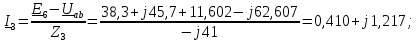 3. Определить показание ваттметра двумя способами: a) с помощью выражения для комплексов тока и напряжения на ваттметре: Активная мощность P двухполюсника, характеризуемого комплексом тока I и комплексом напряжения U, определяется выражением: 𝑃 = (𝑈∙𝐼̃) где 𝐼̃ – сопряжённый комплекс тока, 𝑅𝑒𝑍– действительная часть числа 𝑍. Ваттметр на рис. 1 включён так, что измеряет активную мощность участка (двухполюсника), расположенного справа от ваттметра. Комплекс тока этого двухполюсника I1 , комплекс напряжения Uab . Подставив числовые значения, получим: 𝑃 = 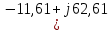 )( )(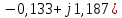 = -72,8 (Вт) = -72,8 (Вт) поформуле UIcosφ: Стрелка ваттметра отклоняется на величину, равную UIcosφ, где U - действующее напряжения на обмотке напряжения ваттметра, I – действующее значение тока, втекающего в обмотку тока ваттметра, φ – угол сдвига фаз между током и напряжением. В рассматриваемом случае (рис. 1) напряжение на обмотке напряжения ваттметра uab, ток, втекающий в обмотку тока i1. Действующие значения: Uab = |Uab| = |-11,61 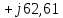 | = 63,7 (В); | = 63,7 (В); I1 = |I1 | = | 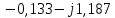 | = 1,19 (А); | = 1,19 (А); Угол сдвига фаз между током и напряжением φ равен разности начальных фаз напряжения и тока: φ = ψUab − ψI1 = arctg ImUab /ReUab - arctg ImI1 ReI1 = arctg 62,61/-11,61- − arctg 1.187/0,133 =-79,50-83,60 = -163° Тогда активная мощность: P = Uab ∙ I1 ∙ cos φ = 63,7∙ 1,19 ∙ cos -163° =-72,5 (Вт) На векторной диаграмме тока и напряжения ваттметра укажем угол φ=φu-φi. На комплексной плоскости построим векторы Uab и I1 . Исходя из величин действующих значений Uab и I1 , выберем следующие масштабы для векторов напряжения и тока: mI = 0,2 А/ см ; mU = 1 В /см Векторная диаграмма изображена на рис. 2.   Uab    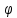 ψUab   +1 ψI1 I1 Рис. 2. 4. Построим векторную топографическую диаграмму токов и напряжений. Векторная топографическая диаграмма токов и напряжений – это изображение на комплексной плоскости векторов всех токов и напряжений на всех элементах цепи. Причём векторы напряжений должны быть расположены в том же порядке, что и элементы цепи. Рекомендуется сначала разместить на комплексной плоскости точки, соответствующие комплексным потенциалом всех точек цепи, а потом соединить соседние точки. Тогда каждый отрезок диаграммы будет соответствовать элементу цепи. Выберем за уровень отсчёта потенциала точку b на рис. 1: 𝜑𝑏 = 0. Потенциалы остальных точек найдем путём подсчёта изменения потенциала при движении от точки b φa = φb + Uab = Uab = -11,6+j62,6; φm = φb +E4 =-15,6+j27; φa= 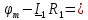 -15,6+j27-30( -15,6+j27-30(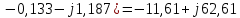 ; ;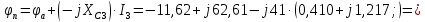 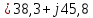 ; ;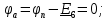     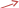  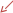          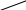      I1∙100 I3∙100 I2∙100 φb φb φn φa φm 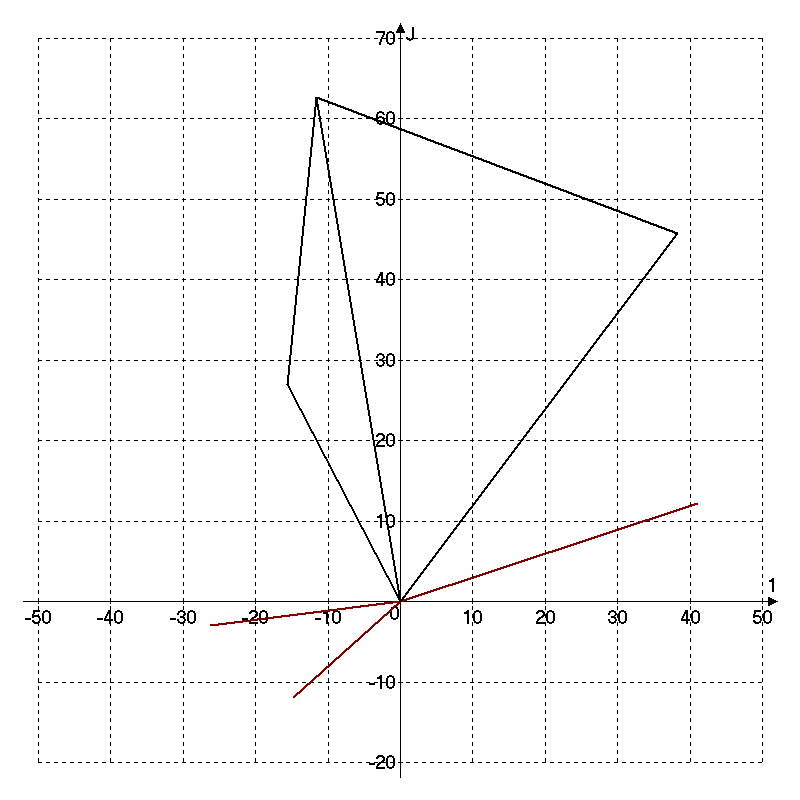 Рис. 3. Рис. 3. 5. Запишем выражение для мгновенного значения тока i1 и по- строить график зависимости i1(ωt) в интервале от 0 до 2π. Выражение для мгновенного значения тока имеет вид: i = Imsin(ωt + ψI ) где Im = √2I – амплитуда тока; 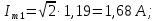 I – действующее значение; I1 = 1,19; ω = 2πf – угловая частота; ψI – начальная фаза тока; ψI1 = arctg arctg -1.187/0,133 =-83,60=-1,46 (рад).  График этой функции рис.4 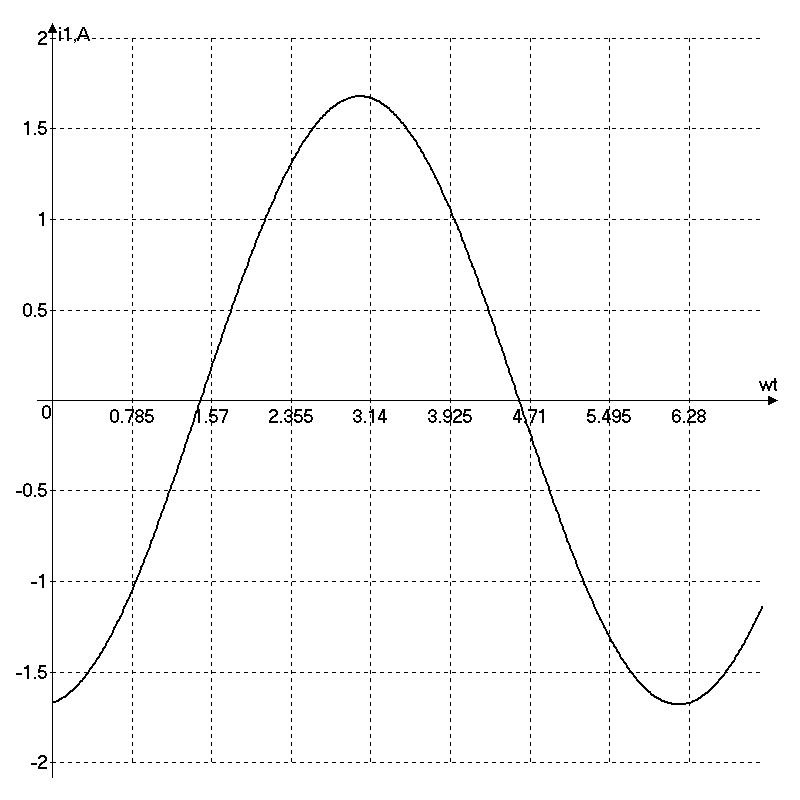 Рис.4 |
