уравнения. дифференциальные уравнения движения линейной. Дано Решение
 Скачать 233.5 Kb.
|
|
Задание 5 Составить дифференциальные уравнения движения линейной колебательной системы с несколькими степенями свободы. Найти собственные частоты колебаний. Катки и колеса считать сплошными однородными цилиндрами, катящимися без скольжения по соприкасающимся с ними телам. Дано: 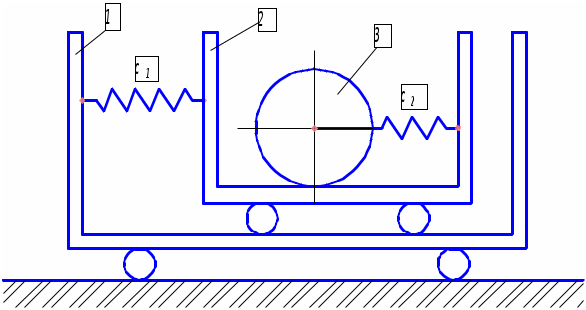 ; ; ; ;  Решение: Данная механическая система имеет две степени свободы, поэтому в качестве обобщенных координат выберем перемещение тела 1 и перемещение тела 3, то е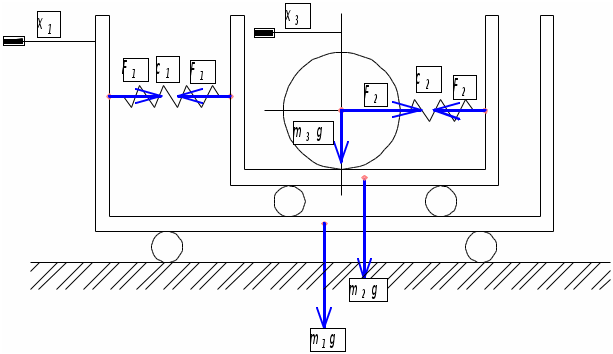сть  ,  . Найдем статические деформации упругих элементов (пружин).  Пусть  − величины деформаций (например, деформаций растяжения) пружин 1 и 2 в равновесном положении системы. Запишем выражения для величин упругих сил, действующих на тела: ,  Найдем кинетическую энергию системы.  ,где  – кинетическая энергия тележки 1, движущейся поступательно;  – кинетическая энергия тележки 2, движущейся поступательно;  – кинетическая энергия катка 3, движущегося плоскопараллельно.    – момент инерции катка 3Выразим скорости центров масс тележек и угловые скорости колес через обобщенные скорости.   Подставляя все в выражение для кинетической энергии, получаем: 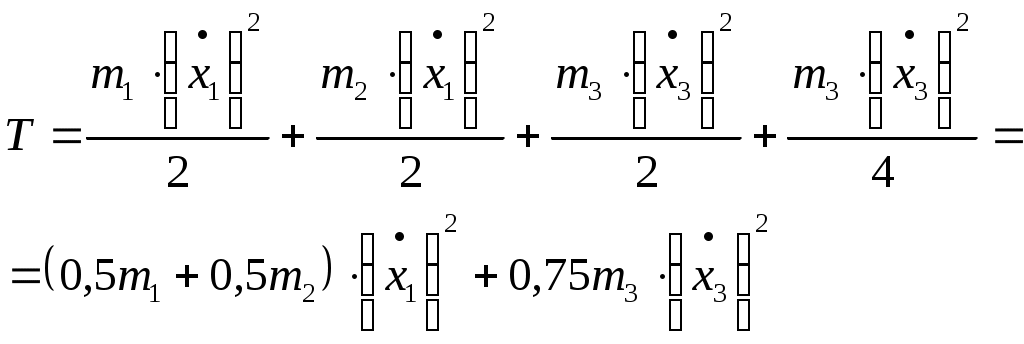 (1)Обозначим: 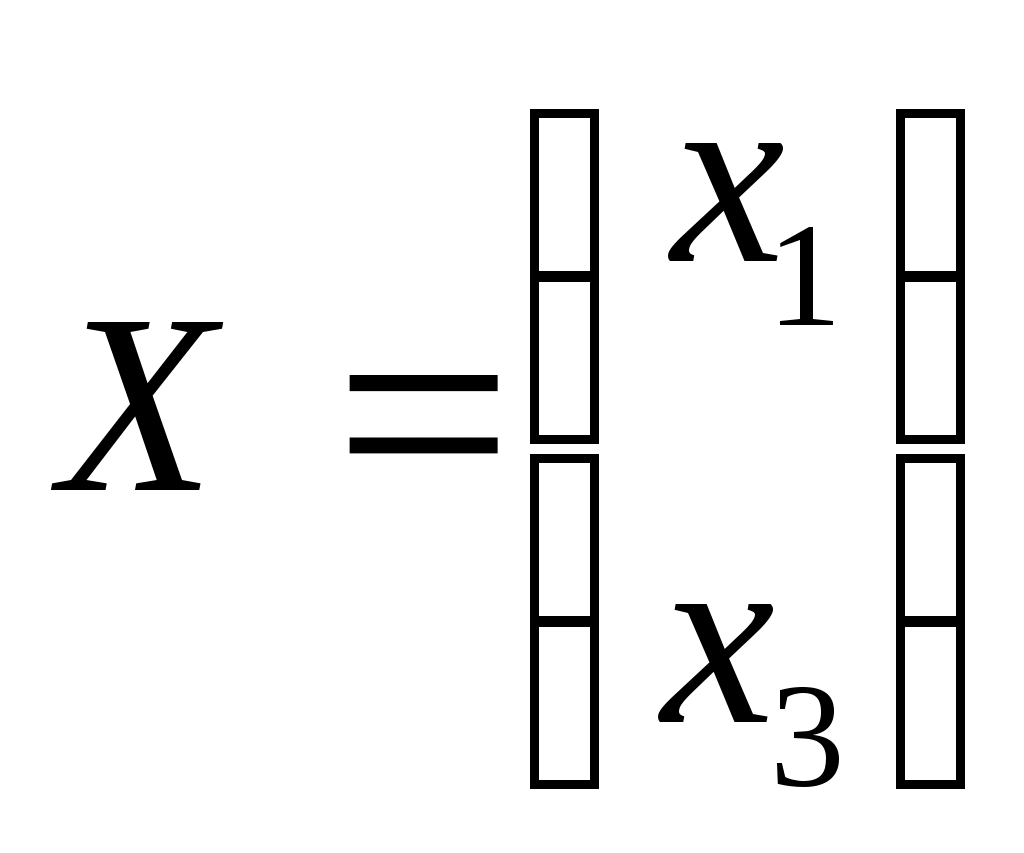 ,  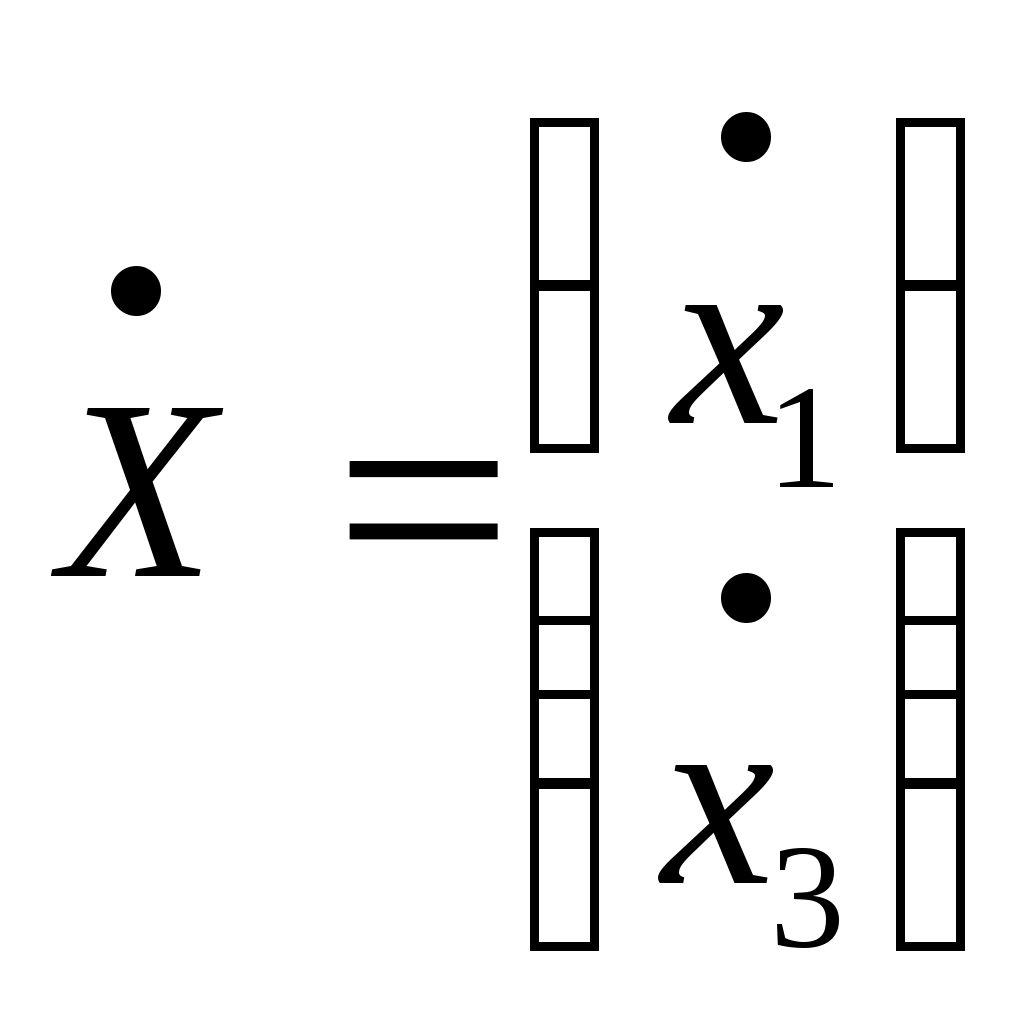– векторы-столбцы обобщенных координат и обобщенных скоростей. Представляем кинетическую энергию в матричной форме:  ,где  – транспонированный вектор  . Составляем матрицу инерционных коэффициентов: 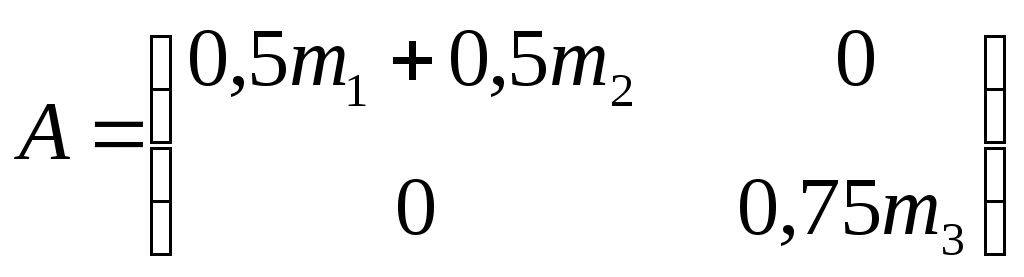 Найдем потенциальную энергию системы. При движении тел работу совершают силы упругости. Потенциальную энергию системы в положении равновесия полагаем равной нулю. Потенциальная энергия есть работа, совершаемая силой поля при возвращении объекта в пространстве обобщенных координат на поверхность нулевого уровня энергии. Поэтому:  В выражении потенциальной энергии каждой пружины фигурирует разность квадратов деформаций в момент времени t и в положении равновесия. Тщательно выписываем деформации, например:  . С увеличением координаты x1 пружина 1 растяивается, т.е. приобретает деформацию противоположного смысла, нежели 1, которая, согласно договору, есть деформация сжатия. Имеем далее:  .Получаем следующее выражение для потенциальной энергии:  Упрощаем это выражение, раскрывая скобки и приводя подобные члены.  Получили потенциальную энергию как квадратичную форму обобщенных координат. Представляем ее в матричном виде:  ,где матрица упругих коэффициентов имеет вид: 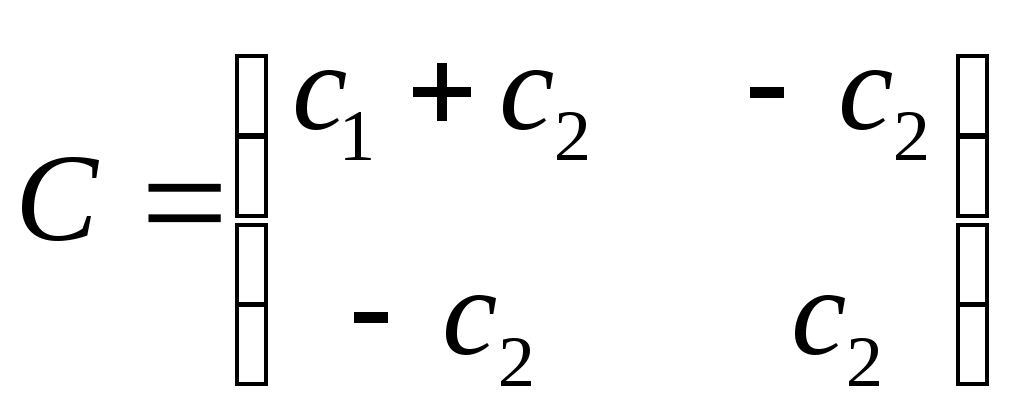 .В матричной форме дифференциальные уравнения движения записываются в виде:  В развернутой форме получаем: 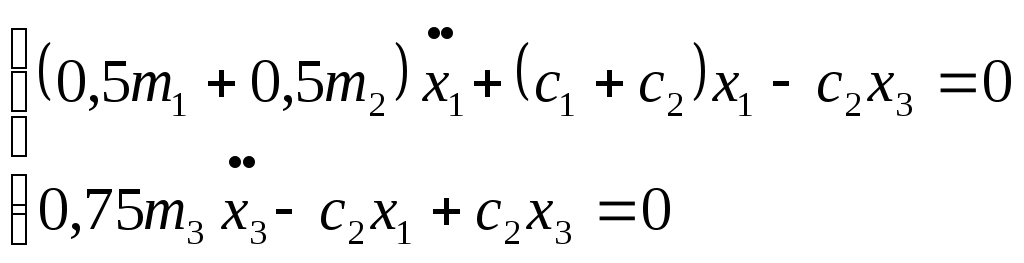 или 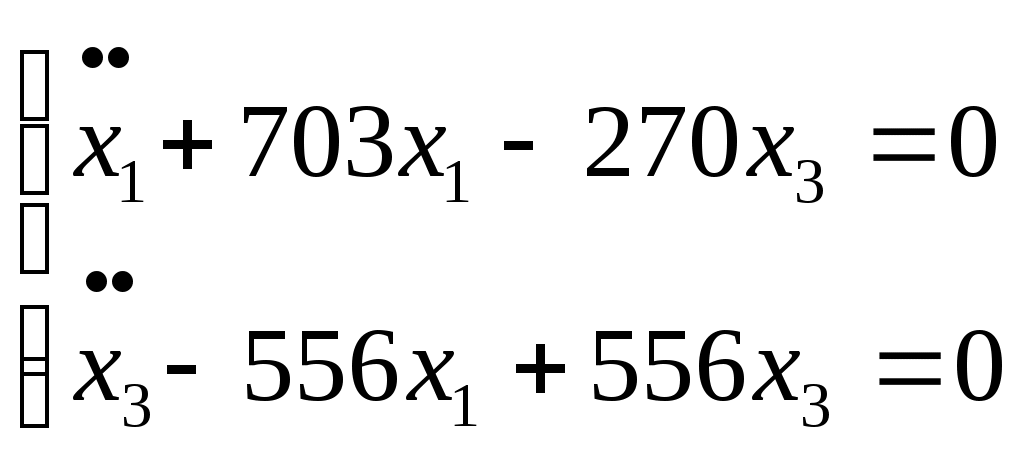 Составляем частотное уравнение:  или  Решаем это уравнение как квадратное относительно 2:  и после извлечения корней получаем   Ответ: 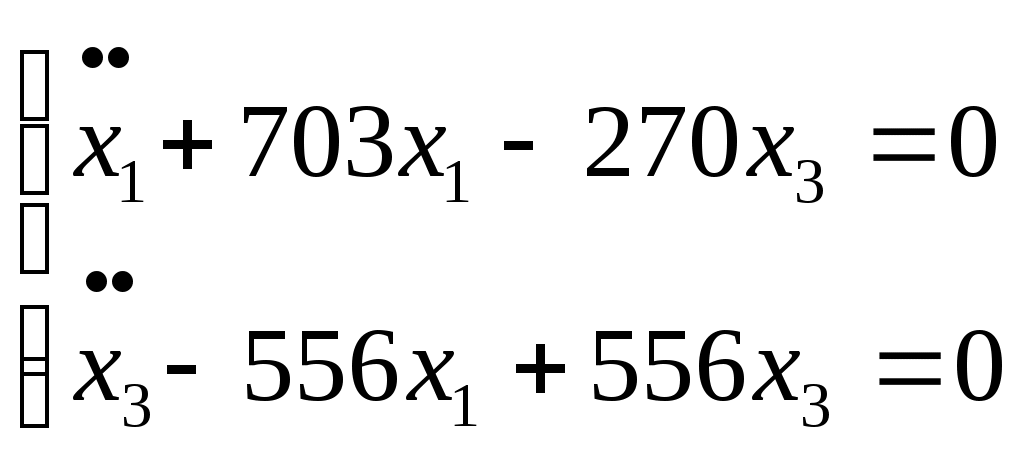|